數學建模素養評價體系的構建與實踐
吳啟虎

【摘要】數學是培養學生數學建模素養的基礎課程,問題是數學的心臟,可見數學問題與數學建模有著密切的關系.基于數學建模過程分析,用解決問題培養學生數學建模素養,同時通過數學建模用數學眼光看待世界,對核心素養在數學教學中有效實施具有實踐意義.
【關鍵詞】初中數學;數學建模;素養評價
數學是一門抽象概括客觀現象的科學語言和工具,數學學科的工具性集中體現在數學建模、用模上,數學建模就是為了解決實際問題.因此,構建全面客觀的指標體系對學生在問題解決中數學建模素養進行評價,提出針對性教學策略,促進學生數學建模素養發展,對數學教學實踐意義重大.
1 數學建模素養評價綜述
數學建模是學生體驗和理解數學與世界的聯系的過程,將現實世界和數學世界打通聯系,用數學眼光看待世界,用數學模型解決現實問題[1].學者們提出經典數學建模內涵,如Niss(1991)數學建模七階段循環[2]、Initiative(2010)數學建模四階段循環[3]、PISA(2021)數學建模三階段循環[4]等,覆蓋數學建模的數學化、數學求解、數學解釋三個關鍵環節,強調數學問題解決中數學化的問題表述,數學問題解決后需要解釋還原問題情境,尋求最終答案.
國內學者們提出不同視角的數學建模素養評價框架,如朱婭梅(2018)構建了含有“情境-過程-內容-水平”的四要素數學建模能力評價框架,并從低到高劃分了“再現-聯系-反思”三個數學建模能力水平.魯小莉等(2019)建立了融合過程性和結果性數學建模能力評價框架,呈現實際情境-情境模型-數學模型-數學解答-解釋與檢驗-實際結果的完整數學建模流程,并針對五狀態和四環節提出六個層級建模水平,兼顧學生數學建模所經歷的關鍵步驟和數學建模子能力水平.邵光華等(2020)結合新課標重新構建了數學建模水平劃分要求和表現一致的數學建模素養評價模型,并結合具體數學建模案例說明模型評價過程.
本文借鑒研究成果,完善評價體系用以有效評估學生數學建模素養,是亟待面臨的關鍵問題,具有重要研究意義.
2 問題解決中學生數學建模素養評價體系構建
將問題解決中學生數學建模素養看作一個閉環系統,正如《義務教育數學課程標準》指出:“從具體情境或現實生活中抽象出數學問題,利用數學符號建立數學問題中蘊含的不等式、方程、函數等數量關系及變化規律,求出結果、并討論結果的意義.”論文評價體系指標在現有研究成果基礎上,遵循重視學生數學建模素養整體性和階段性評價,關注學生數學建模過程和數學建模素養達成,認為學生數學建模素養評價體系中,準則層包括數學化、建立數學模型、求解數學問題、數學解釋、檢驗模型結果.
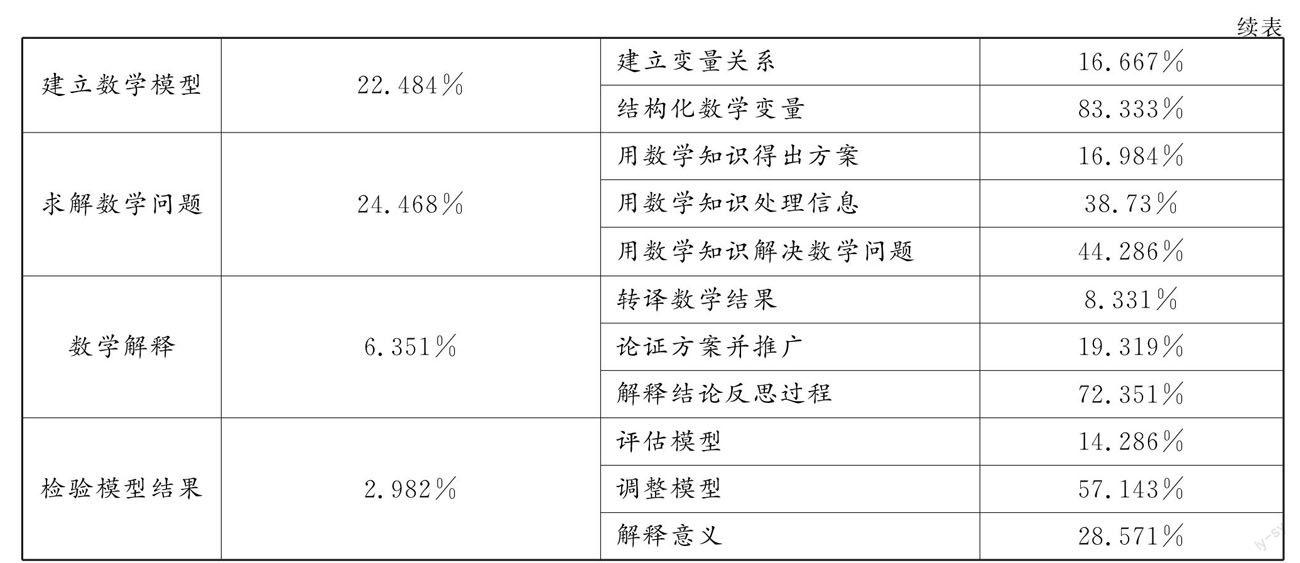
論文邀請5位具有豐富教學經驗的數學一線教師,確定數學建模素養評價體系的合理性和科學性,按照Saaty的標度法對各指標重要性進行判斷打分,構建準則層和指標層判斷矩陣,利用層次分析法在通過一致性檢驗后得出各指標權重,最終問題解決中數學建模素養評價體系指標權重如表1所示.
3 案例分析
3.1 數學建模題測試
本文利用典型初中數學建模題對學生數學建模素養進行評價,數學建模題滿分100分,其中第一題為手拉手模型,30分,第二題為將軍飲馬模型,30分,第三題為阿氏圓模型,40分.
數學建模測試中,要求學生嚴格按照數學建模過程書寫,寫明題目分析過程,解題過程和反思結論,便于教師打分計算.
3.2 數據來源
選擇徐州市毛莊中學初三學生作為研究樣本,基于已構建的學生數學建模素養評價指標體系,對測試題的標準答案進行量化表述,確定各測試題打分標準.每道題按照打分標準由教師進行各指標量化統計,初步篩選出學生的有效成績.
本次測試共發出100份測試題,經過篩選有效成績87份,對學生成績進行信度和效度分析,結果顯示各指標校正項總計相關性(CITC)均大于0.5,Cronbach α系數為0.76,說明問卷信度較好;KMO值為0.744,p值為0<0.05,說明問卷效度良好.
3.3 成績計算
教師對學生測試成績按照數學建模指標體系進行打分,統計結果顯示:變異系數反饋轉譯數學結果、評估模型、確定數學參數和變量三個指標成績最差,其中確定數學參數和變量指標的成績均值低于中位數,需要重點關注.并且,確定數學參數和變量指標的統計置信區間CI值差異值為1.657,是所有指標中最大,因此估計可靠性不好,意味著學生該指標成績極不穩定.
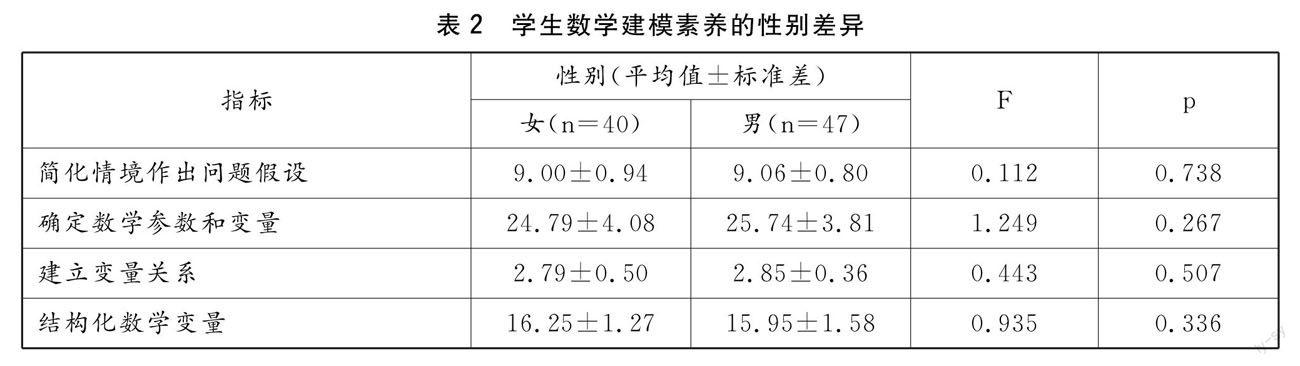
利用方差分析學生數學建模素養的性別差異,統計如表2,結果顯示:不同性別學生對簡化情境作出問題假設,確定數學參數和變量,建立變量關系,結構化數學變量,用數學知識得出方案,用數學知識處理信息,解決問題,轉譯數學結果,論證方案并推廣,解釋結論反思過程,評估模型,調整模型12個指標未表現出顯著性差異,對解釋意義指標呈現顯著性差異.
4 對策
4.1 “確定數學參數和變量”素養教學建議
數學化是學生將問題情境簡化后,能夠從存在多變量的問題中確定合適的參數和變量,從而揭示問題情境背后的數學關系,讓問題解決變得簡單清晰.建議:(1)加強學生審題閱讀能力,培養學生處理題干關鍵信息的自信和能力.閱讀是審題的必備能力,是數學建模首要環節,通過審題從問題中抽象出問題本質,對題干大量信息進行有效處理提取,抓住要害、分清主次,簡化問題情境,學會抽取數學信息,形成穩定建模思維.(2)給學生留有充足的思考空間.初三學生接觸了初中階段所有的數學模型,但是他們還難以從問題情境中快速反應出數學模型.因此,教師應給學生留足思考空間,引導學生認真觀察分析,相機對學生進行點撥引導,思考一般數學模式表達,讓學生慢慢體會和理解數學建模過程,鍛煉學生對問題情境進行歸類,尋找題目中已知存在范圍和待求解范圍的量,確定數學參數和變量,找準問題解決切入點.
4.2 “結構化數學變量”素養教學建議
初三學生能否理清問題情境中各參數和變量的數學關系是影響結構化數學變量的主要原因,且指標相對權重較大.建議:(1)引導學生分解問題情境,確定數學問題難點.學生從題目已知存在范圍的量抽象出變量,待求解范圍的量定義為參數,教師再引導學生從簡化后的問題情境中,還原數學問題,學生更容易理解問題所屬數學模型,結合題目信息類型,建立起模型關聯.(2)師生互動交流教學,促進學生實踐體驗學習.教師通過實踐活動,幫助學生將所學數學知識和思想方法內化,轉化為數學思維,在問題情境中相互交流探討,帶領學生再發現、創造知識,體驗數學信息和數據的收集處理過程,從實際問題中構建數學模型,慢慢應用數學工具建立數學參數和變量的關系,體驗數學建模過程,解決實際問題、解釋回答實際問題,真正掌握結構化數學變量能力.
4.3 解釋意義方面教學建議
基于性別差異提出“解釋意義”素養教學建議:注重數學的生活應用價值教學.數學源于生活,現實生活中有很多數學建模問題,選取生活中數學建模案例進行練習,引導學生從現實情境中體會數學建模在身邊,學生利用所學數學知識解決實際問題,體會數學的生活應用價值.教師鼓勵學生用數學的眼光看待世界,從數學角度解決生活問題,讓數學學以致用,加強生活和數學聯系,提高數學建模解釋意義素養.
參考文獻:
[1]郭良秋.學生“數學建模”素養培養例談[J].中學教學參考,2021(35):21-22.
[2]姬梁飛.數學建模素養:應力場域、構成要素與生成路徑[J].教師教育學報,2021,8(06):98-106.
[3]魯小莉,程靖,徐斌艷,王鴦雨.學生數學建模素養的評價工具研究[J].課程.教材.教法,2019,39(02):100-106.
[4]董潔,沐方華.基于新課標的數學建模能力評價探討[J].中學數學教學,2019(05):1-3.

