思維導圖輔助初中數學解題教學研究
崔玉民

【摘要】本文將以思維導圖為中心,首先分析現階段思維導圖在初中數學解題教學中的應用問題,最后結合例題提出相應的應用策略及措施.
【關鍵詞】思維導圖;初中數學;解題教學
1 思維導圖制作過程中關鍵字詞整理
思維導圖在輔助初中數學解題教學過程中抓取和整理關鍵字詞顯得尤為重要.在復習中,引入以圓為關鍵字詞的復習思維導圖(如圖1所示),然后進行題目練習,解題教學質量會事半功倍.
引入以下題目,引導學生結合思維導圖解答.
如圖2所示,以AB為直徑的圓O分別于BC,AC相交于點D,E,BD=CD,過點D作圓O的切線交邊AC于點F.
求 (1)求證:DF⊥AC;
(2)若圓半徑為5,∠CDF=30°,求BD弧長(結果保留π).
教學分析 從第一問進行分析,從關鍵詞的抓取出發,結合題目當中的相關敘述得到條件,O,D分別位于線段AB,BC的中點,所以連接OD,OD則是△ABC的中位線,以D為切點,即能夠證明;從第二問進行分析,已知∠CDF=30°,∠ODF=90°,r=5,從關鍵詞進行聯系,則可以推出△BOD為等邊三角形,然后從結合弧長公式則能夠得到答案.
解 (1)因為DF是圓O的切線,D為切點,
所以OD⊥DF,
所以∠ODF=90°,
因為BD=CD,OA=OB,
所以OD是△ABC的中位線,
所以OD∥AC,
所以∠CFD=∠ODF=90°,
DF⊥AC.
(2)因為∠CDF=30°,
由(1)得∠ODF=90°,
所以∠ODB=180°-∠CDF-∠ODF=60°,
因為OB=OD.
所以∠OBD=60°,
所以△BOD是等邊三角形,
∠BOD=60°,
所以BD弧長為60°πR180=53π.
題目總結 根據題目所知第一問主要考查圓與三角形中位線相關的知識點,第二問主要考查弧長公式的運用,所以在解題教學之前,教師應該注重將二者運用思維導圖進行連接,帶領學生對此類知識點進行回顧,再開展教學.
2 豐富思維導圖制作過程中個性化設計
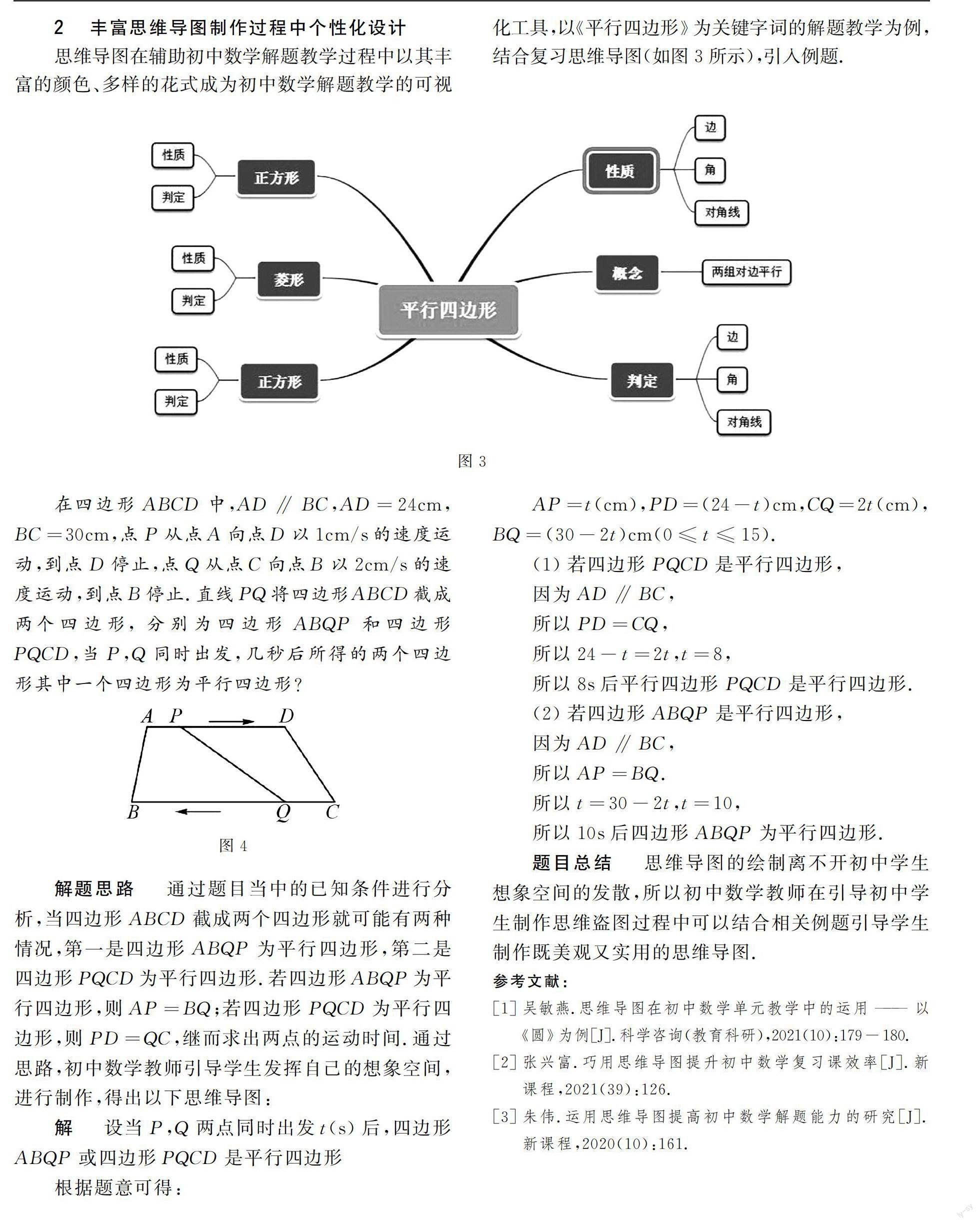
思維導圖在輔助初中數學解題教學過程中以其豐富的顏色、多樣的花式成為初中數學解題教學的可視化工具,以《平行四邊形》為關鍵字詞的解題教學為例,結合復習思維導圖(如圖3所示),引入例題.
在四邊形ABCD中,AD∥BC,AD=24cm,BC=30cm,點P從點A向點D
以1cm/s的速度運動,到點D停止,點Q從點C向點B以2cm/s的速度運動,到點B停止.直線PQ將四邊形ABCD截成兩個四邊形,分別為四邊形ABQP和四邊形PQCD,當P,Q同時出發,幾秒后所得的兩個四邊形其中一個四邊形為平行四邊形?
解題思路 通過題目當中的已知條件進行分析,當四邊形ABCD截成兩個四邊形就可能有兩種情況,第一是四邊形ABQP為平行四邊形,第二是四邊形PQCD為平行四邊形.若四邊形ABQP為平行四邊形,則AP=BQ;若四邊形PQCD為平行四邊形,則PD=QC,繼而求出兩點的運動時間.通過思路,初中數學教師引導學生發揮自己的想象空間,進行制作,得出以下思維導圖:
解 設當P,Q兩點同時出發t(s)后,四邊形ABQP或四邊形PQCD是平行四邊形
根據題意可得:
AP=t(cm),PD=(24-t)cm,CQ=2t(cm),BQ=(30-2t)cm(0≤t≤15).
(1)若四邊形PQCD是平行四邊形,
因為AD∥BC,
所以PD=CQ,
所以24-t=2t,t=8,
所以8s后平行四邊形PQCD是平行四邊形.
(2)若四邊形ABQP是平行四邊形,
因為AD∥BC,
所以AP=BQ.
所以t=30-2t,t=10,
所以10s后四邊形ABQP為平行四邊形.
題目總結 思維導圖的繪制離不開初中學生想象空間的發散,所以初中數學教師在引導初中學生制作思維盜圖過程中可以結合相關例題引導學生制作既美觀又實用的思維導圖.
參考文獻:
[1]吳敏燕.思維導圖在初中數學單元教學中的運用——以《圓》為例[J].科學咨詢(教育科研),2021(10):179-180.
[2]張興富.巧用思維導圖提升初中數學復習課效率[J].新課程,2021(39):126.
[3]朱偉.運用思維導圖提高初中數學解題能力的研究[J].新課程,2020(10):161.

