巧用數學實驗 做“好玩”的數學
——以“3的倍數的特征”為例

江蘇省揚大教科院附屬楊廟小學 王興偉

一、問題提出

眾所周知，教學“3的倍數的特征”的關鍵是如何從觀察數的末尾數字轉到觀察所有數字的和，這是一個轉折，更是一個跨越。課堂上，有的教師用精美的課件將復雜的特征推導過程演示得清清楚楚，有的教師非常順利地得出3的倍數的結論，有的教師則干脆省去所有繁雜的過程，直接告訴學生3的倍數的結論。在這樣的課堂上，學生學得機械、枯燥，感受不到知識本身的奇妙和魅力。如何在有效建構3的倍數的概念的同時避免先前學習的負遷移？如何引領學生從關注概念的外表轉向思考內在的本質，進而指向學生的抽象、推理等核心素養？面對這些問題，筆者采用了數學實驗教學的方法，既激發了學生的學習興趣，又培養了學生良好的探究性學習習慣，提升了學生的自主創新能力。

二、課堂回放

（一）首次實驗，用四顆算珠撥數，激起疑惑

師：同學們，我們都知道判斷一個數是不是2、5的倍數，要看個位上的數。今天，我們來研究3的倍數，你猜想什么樣的數是3的倍數？

（學生有的猜想個位上的數是3、6、9，有的猜想個位上的數是0、5、…）

師：究竟看什么呢？我們來驗證一下。這是一張1～50的數表，請大家圈出是3的倍數的數，觀察圈出的數，思考一下，求3的倍數的數，只看個位上的數，對嗎？

（學生圈過后發現有的個位上是3、6、9的數是3的倍數，有的卻不是，是3的倍數的數在個位上的數有0~9，不能只看個位上的數）

師：3的倍數到底與什么有關呢？我們一起來做一個小實驗——撥珠實驗。

活動要求：

（1）用4顆算珠撥3的倍數。

（2）同桌兩人合作，一個人撥珠，另一個人判斷它是不是3的倍數（可以用計算器）。

（3）把撥的數記在實驗記錄單相應的方格里。（見表1）

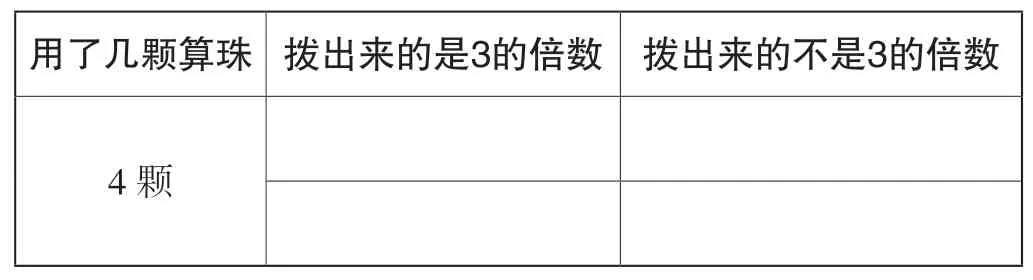
表1 實驗記錄單（一）

（生合作實驗，師巡視，完成后組織匯報交流）

生1：我撥了一個211，它不是3的倍數。

生2：我撥了一個31，它也不是3的倍數。

……

（教師把學生匯報的數輸入屏幕的表格中）

師：有沒有人撥出的數是3的倍數？大家都沒有撥出3的倍數，這說明什么問題呢？

生：用4顆算珠撥不出3的倍數。

師：是啊，剛才撥珠時，有的同學把4顆算珠分散在幾個數位上，有的同學干脆放在一個數位上，可無論怎樣撥，都撥不出3的倍數。

策略分析：用實驗的方法不但提高了數學知識本身的趣味性，而且讓學生經歷了探究“3的倍數的特征”的過程。學生從觀察數的末尾的特征到觀察這個數的數字和，具有很大的思維跨度，很難獨立通過研究發現3的倍數的特征。教師通過預設一個“陷阱”，讓學生經歷撥珠后發現，4顆珠子無論怎么撥都撥不出3的倍數。這時，學生在操作中自然就會產生疑惑：“為什么4顆珠子就撥不出3的倍數呢？如果用其他數量的算珠呢？”困惑越大，探究的欲望就越強烈，不待教師吩咐，學生已迫不及待地進入下一個環節的學習。

（二）第二次實驗，用任意顆算珠撥數，整體感知

師：既然用4顆算珠撥不出3的倍數，那么，究竟要幾顆算珠才可以撥出？下面，同桌兩人商量一下，任意選擇幾顆算珠，一個人撥，另一個人記錄并填寫在實驗記錄單里，然后判斷它是不是3的倍數。

（生同桌合作活動，教師巡視、指導，然后讓學生帶著實驗記錄單再次反饋交流）

（學生匯報時有的用了3顆算珠撥數，有的用了4顆、5顆、6顆……同時，學生發現，只要是用了3顆、6顆算珠撥的數，都是3的倍數，而用了4顆、5顆算珠撥的數，都不是3的倍數）

師：用3顆算珠能撥出哪些數呢？

生:我們撥出了30、21、12、120、102、210，它們都是3的倍數。

（師相機板書：30、21、12、120、102、210）

師：從這三個數上怎么能看出是用了3顆算珠呢？

生：“102”百位上的“1”用了1顆珠子，十位上是“0”，沒用珠子，個位上是“2”，用了2顆珠子，一共用了3顆。“21”這個數也是一樣的道理。

（師板書：1+0+2=3， 2+1=3）

師：有沒有用3顆珠子撥出一個不是3的倍數的數呢？

生：沒有。

師：我們再來看看用5顆算珠撥出的數，哪些同學是用5顆算珠撥數的呢？

生：我們用5顆珠子撥了一個320和11111，它們都不是3的倍數。

……

師：有沒有人用5顆珠子撥出一個是3的倍數的數呢？

生：沒有。

師：還有誰用了幾顆算珠撥數？撥出的情況怎樣？

生：我們用了6顆，撥出的數是51、3300、420，它們都是3的倍數。

師：同學們，誰能看出他是用了6顆算珠撥數的？

生1：“420”百位上的“4”用了4顆珠子，十位上是“2”，用了2顆珠子，個位上是“0”，沒用珠子，一共用了6顆。“321”這個數也是一樣的道理。

生2：我補充一點，各個數位上的珠子可以任意調換順序，但結果都是3的倍數。

（師板書：4+2+0=6， 3+2+1=6）

策略分析：教師安排學生用任意顆算珠撥3的倍數的實驗，通過撥數實驗和全班學生的匯報，使學生進一步發現用4顆、5顆算珠撥數，都撥不出3的倍數，而用3顆、6顆算珠撥數，怎么撥都是3的倍數。學生對3的倍數的特征有了初步感知，在實驗和探究過程中逐步建構起對“3的倍數的特征”的整體認知，而且其認知隨著實驗的不斷深入會越來越清晰。

（三）第三次實驗，用3的倍數顆算珠撥數，驗證推理

師：學到這里，我想請大家再猜想一下，3的倍數的特征可能是什么？

生1：如果算珠是3的倍數，撥出來的數一定是3的倍數。

生2：如果一個數各個數位上加起來是3的倍數，這個數一定是3的倍數。

……

（師相機板書：猜想一，算珠是3的倍數；猜想二，各位數的和是3的倍數）

師：你能說說是怎么想的嗎？

生：用3顆算珠，怎么放都是3的倍數，而用5顆算珠，怎么放都不是3的倍數。

師：這兩種猜想一樣嗎？

生：兩種猜想是一樣的，因為各數位上的數字之和就是算珠的顆數。

師：我們怎樣驗證這些猜想是否正確呢？

生：我們可以再實驗一次，用3的倍數顆算珠去撥數，看它們是不是3的倍數，這樣就可以判斷猜想是對還是錯。

師：好吧，請你任意取一些珠子，但顆數必須是3的倍數，然后任意撥一些數，看看它是否是3的倍數。如果是3的倍數，就請你把撥的數和用了多少顆算珠輸入屏幕上的這個表格中。（師生共同輸入數據，見表2）

策略分析：教師讓學生用任意3的倍數顆算珠撥一些數，并且把大家實驗中的數據輸入實驗記錄單中，這樣做，就可以從特殊推理到一般，彌補了不完全歸納法的不足。學生通過積累大量的表象，激活了思維。當教師給學生大量的機會去觀察、類比、歸納、推理、猜想、驗證、交流的時候，學生就會被數學知識本身的魅力深深吸引。學生通過數學實驗，完整經歷了知識的發生、形成和發展過程，重走了人類發現數學規律的歷程，并從直觀具體的實驗階段走入抽象理論階段，從而達到對數學知識的“再發現”和“再創造”境界。

（四）第四次實驗，用分小棒演示，推理證明

師：剛才我們通過觀察、舉例，知道了3的倍數的特征。這個特征是不是巧合呢？它背后的真相到底是什么呢？要揭開這個秘密，我們可以借助一件神秘武器——小棒來完成。

（師出示123根小棒，要求分成3份，學生口答算式，師板書“123÷3”）

師：想一想，用小棒怎么表示“123”？

生：1捆一百根小棒、2捆十根小棒，再加3根小棒。

師：我們先分百位上的小棒。1捆一百根小棒怎么分成3份呢？還余幾根？

生： 1捆一百根小棒，分成3份，每份33根，共計99根，還余1根。

師：再分十位上的小棒。這里有2捆十根了，我們可以一捆一捆地分。怎么分成3份呢？

生1：第一捆分成3份，每份3根，共計9根，還余1根。

生2：第二捆也一樣，分成3份，每份3根，共計9根，也余1根。

師：那十位上一共就余了幾根？

生：兩根。

師：個位上有3根，我們先將3根小棒單獨放在旁邊。

（師引導學生觀察課件，見下圖）

師：現在要判斷123是否是3的倍數，只要看哪部分？

生：余下的根數。

師：是多少？

生： 1+2+3。

師：觀察一下，這里余下的根數和什么是一樣的？

生：“1”和百位上的數一樣，“2”和十位上的數一樣，“3”就是個位上的數，余下小棒的根數和各位上的數字一樣。

師：現在你知道3的倍數有什么特征了嗎？為什么？

生：因為把各個數位上的小棒分掉后，余下的和各數位上的數一樣，所以要判斷是否是3的倍數，只要看各數位上的數字之和是否是3的倍數。

師：老師只舉了一個數的例子，你們像這樣用小棒再舉一些例子，4人為一個小組，分工合作，用小棒來分一分，在實驗記錄單（見表3）上填一填，然后大家議一議，看看你有什么發現。

表3 實驗記錄單（三）

策略分析：教師通過讓學生進行分小棒的實驗，引領學生去探求3的倍數的特征的根源：為什么各數位上的數字之和是3的倍數，那這個數就是3的倍數呢？用小棒的方法來進行實驗，簡單直觀，一目了然，巧妙的數形結合使學生對高深的原理有了初步的理解，從而解決了學生腦海中的疑惑。學生用自己的方式去“理解算理”，了解知識的“前世”“今生”和“未來”，不僅能豐富知識、開發潛能，還能在探究中學會探究，從而不斷地改善自我、發展自我。

三、分析反思

（一）創設實驗情境，激發探究欲望

數學實驗必須要創設實驗情境，學生在情境中就能形成問題意識，并產生強烈的要解決這一問題的內驅力。同時，教師可以利用情境，使學生原有的數學認知結構與新學習的內容之間發生矛盾沖突，使學生在心理上產生學習需要。在本例中，教師在課的開始先讓學生回憶2、5的倍數的特征，再觀察50以內3的倍數，通過觀察對比，引導學生從正、反兩個方面否定了3的倍數與末尾數字有關的認知。接著，教師讓學生通過用“4顆珠”和“3顆珠”進行對比，使學生在認知沖突中自然產生了強烈的學習需求。這一實驗情境的創設，激發了學生的求知欲望，充分調動了學生學習新知的興趣，促使學生智力活動的潛力得到充分的啟迪、發掘和發揮。

（二）引領親身體驗，調動全員參與

數學實驗的最大特點就是讓學生自己動手、實驗、操作。教學中，學生的“探”在前，教師的“導”在后，課堂中注重的是知識獲得的過程和方法，注重的是對學生探究能力的培養。在本例的實驗活動中，教師為學生設置障礙，讓學生和同伴小組合作闖關。教師以小組成員的身份參與其中，與學生一起實驗、討論、對話，這樣的實驗過程是師生互動的精神生產過程。學生通過四次實驗，在實驗操作中進行猜想、觀察、比較、分析、概括，親身體驗了“3的倍數”的發現過程。在課堂中，每個學生都在玩學具、看特征、找發現，人人動手，個個參與。學生發現的結論無論是淺顯的還是深刻的，都是其最真實的體驗和感受。

（三）逐層漸進建構，建構深度思維

現代教育論認為，學生應重走人類掌握數學的歷程，從直觀具體的實驗階段走入抽象的理論階段。在學生進行自主操作實驗后，教師應及時將學生發現的信息整理歸納，將問題做進一步的引申、拓展，逐步將學生的動作思維提升到言語表征，從具體形象思維引導到抽象邏輯思維，從而培養學生思維的深刻性。本例中的四次實驗活動，不是簡單的重復，而是層層遞進、環環相扣、由表及里，不斷地向概念的核心“挺進”。教師像剝筍一樣，在每次實驗后，將影響“3的倍數的特征”這個概念的外衣層層剝去，不斷激發學生向更上位的方法層面思考，步步逼近概念的核心層。最終，師生一起去發現、探尋“3的倍數的特征”的本質，使課堂教學不僅是學生學習知識的過程，還是師生共同建構概念意義的過程，實現了師生知識共享、情感交流、心靈溝通、能力創新等多層次的互動。