高中校本課程“數學文化”的開發與實踐
——以“人生相遇幾何”為例*

黃 榮 (江蘇省無錫市第一中學 214031)

周 超 (蘇州大學數學科學學院 215006)

《普通高中數學課程標準(2017年版)》(下稱《課標2017》)明確提出，要重視數學文化，將數學文化融入課程內容[1]，從而在課程結構的高度上確立了數學文化的重要地位.但當前教學仍存在過多關注于學科價值而忽視數學應有的科學價值、應用價值、文化價值和審美價值[2]的現象.筆者將近年來執教校本課程“數學文化”的系列思考整理成文，與同行分享課程開發與實踐的經驗.

1 開發校本課程“數學文化”的整體設計

課程的開發與實踐是一種系統化的活動，需要從全局高度對“數學文化”課程作出整體設計，主要包括課程的理念、目標、內容、實施與評價等.

1.1 課程理念定位：聚焦“文化育人”

一方面，教科書中呈現的數學往往只有“冰冷的美麗”，知識背后的美輪美奐仍亟需挖掘；另一方面，課程標準賦予數學學科的價值是多方面的.“數學文化”課程應當充分挖掘數學的多元教育價值，以“文化教學”促動學生“火熱的思考”[3]，實現從“知識育人”走向“文化育人”.

1.2 課程目標設置：提升數學素養

“數學文化”課程并非定位于普及數學知識的學科課程，其核心不在于具體的數學知識本身.要更多關注數學知識的形成和發展，關注數學產生與應用的跨學科特性，即關注數學在人類生活、科學技術、社會發展中的重大貢獻和價值[1][4].因此，“數學文化”課程重在以數學知識為載體，豐富教學內容，促使學生感悟數學的多元價值，進而提升數學素養，涵養理性精神和人文情懷.

1.3 課程內容選取：主題引領，精選內容

課程內容的選取需要考量多方面因素，課程的理念和目標、學情、教師的知識儲備、可獲得的學習資源等.[5]校本課程作為選修課，課時較少，選課學生來自不同班級，數學基礎差異較大.因此，課程內容選取應優先考慮初高中銜接點和高中必修課程內容，以此為生長點精選內容、引申拓展，進而形成若干主題.

數學文化包含知識系統、工具系統、價值系統和史實系統四個層面的內容，知識系統是物質基礎，工具系統體現數學應用，價值系統是發揚數學文化的源泉，史實系統是數學文化的歷史積淀.[6]

基于上述理解，筆者將“數學文化”課程劃分為五大主題：預備知識、數學史話、數學之用、數學之美、數學寫作.各專題均以知識系統為載體(而非目的)，側重于數學文化的某個層面：預備知識是緒論，帶領學生初識數學文化；數學史話側重史實系統，體現數學的科學價值；數學之用側重工具系統，體現數學的應用價值；數學之美側重價值系統，體現數學的審美價值；數學寫作則是一種綜合性的創作實踐.具體內容如表1所示.

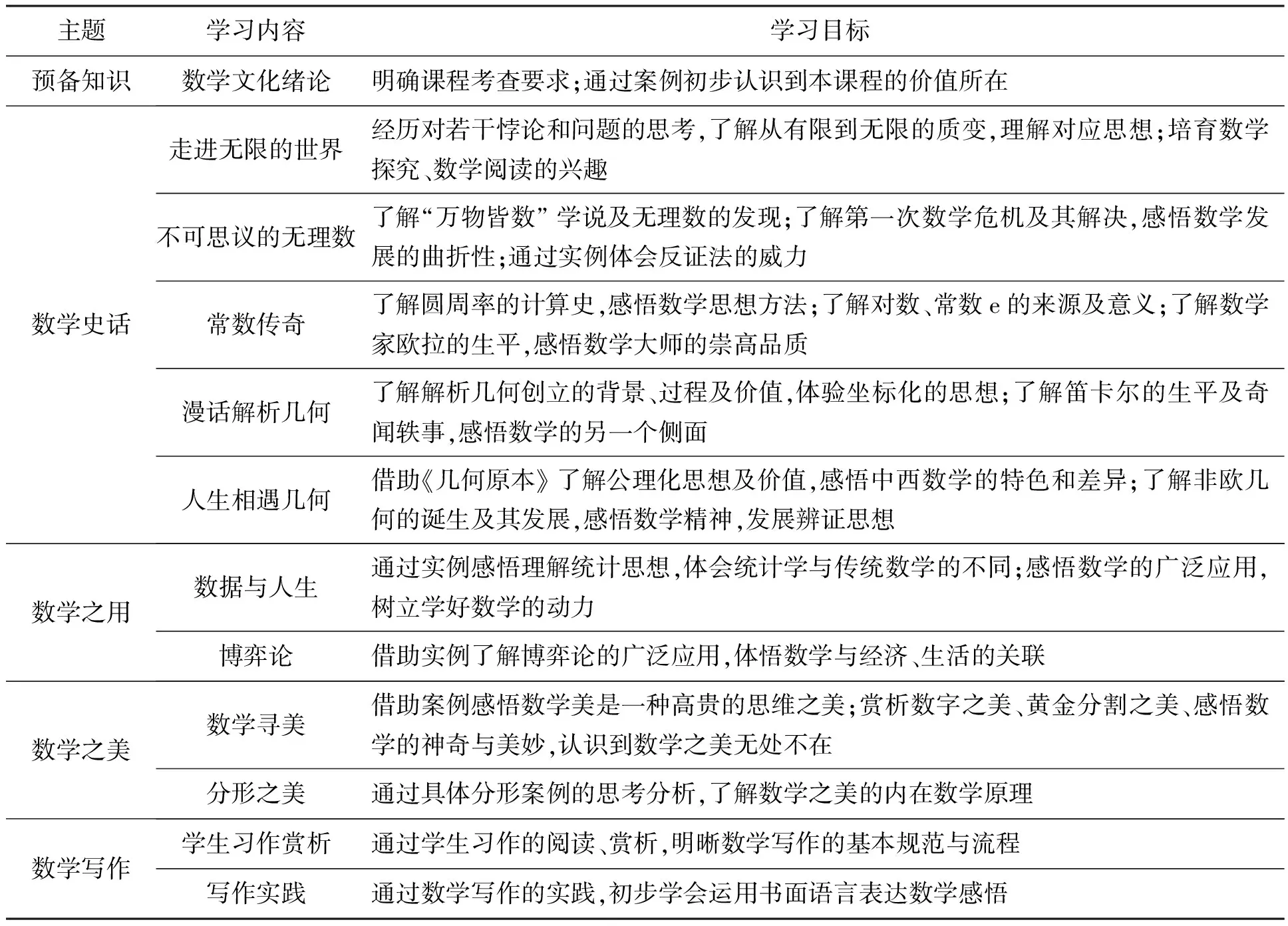
表1 校本“數學文化”的主題、內容及目標

5個主題共12小節，每節安排1-2課時，可視情況增刪，共需14-18課時學完課程.

1.4 課程實施策略：凸顯四性，增強體驗

在實施“數學文化”課程時應著力凸顯“四性”，即趣味性、人文性、應用性、思想性[7]，重視增強學生的參與和體驗，激勵學生表達內心的真實感悟和思考.

如“走進無限的世界”[7]，順著數學史的發展脈絡，帶領學生穿越時空，對話數學大師，以“阿基米德與烏龜賽跑”“伽利略悖論”“希爾伯特旅館”系列數學問題引發學生思考，這些問題兼具趣味性、人文性和思想性，可以幫助學生逐步理解對應思想，體悟有限與無限的差異.

再如“數據與人生”，先從生活中的統計問題說起，感受身邊的數據“謊言”；再以語言學字頻研究和二戰史實為例講述統計的應用；最后以案例“公說公有理，婆說婆有理”和選舉悖論結尾引發深度思考，留下回味空間.縱觀整個教學流程，學生充分參與研討，在思考中養成正確的統計思維，體悟到數學的廣泛應用.

1.5 課程評價設計：重視過程，多元評價

作為校本課程，“數學文化”課程不宜采用書面考試作為評價方式，而應重視過程性評價，并采用多元化的評價方式，以評價提升學生學習數學文化的積極性.評價應關注課堂參與度，可適時記錄學生交流的頻次和深度；學生按意愿組成學習小組，開展交流合作，進行小組評價.此外，課程要求遞交期末論文一篇，學生根據參考選題，自擬標題撰寫論文.該論文的評價將依據自我評價、小組評價和教師評價形成綜合等級評價，各小組優秀作品會在班級交流展示.

2 校本課程“數學文化”開發案例——人生相遇幾何

《課標2017》將幾何學的發展列入選學內容(不作考試要求)[1].事實上，歐氏幾何作為中小學數學的重要內容，在培養邏輯思維、涵養理性精神方面起著難以替代的作用[8]；非歐幾何雖非高中必修內容，但在轉變數學認知，樹立正確的數學觀方面也極具教育價值[9].因此，筆者將兩者整合成一節“人生相遇幾何”，以期幫助學生整體認知幾何學，樹立正確的數學觀.

2.1 教學內容分析

本節內容主要包括兩方面：一是幾何原本與公理化思想，二是非歐幾何與真理的相對性.公理化思想是現代數學的基本特征，非歐幾何是幾何領域的重大革命，這些內容的教學有利于形成正確的數學觀、科學觀，是不可多得的優秀數學文化素材.

2.2 教學目標分析

基于關注數學基本思想和多元價值、厚植理性精神和人文情懷的課程目標定位，將本節內容目標定位如下：

(1)通過學習《幾何原本》，了解公理化思想的基本特征及其在數學、科學、文化中的價值，并通過中西數學特色的對比感悟文化差異；

(2)了解非歐幾何誕生及其發展的基本歷程，感受數學家明理崇真、百折不撓的精神品質，體悟數學作為真理的相對性，發展辯證思維.

2.3 教學實施分析

為增強學生體驗，并兼顧數學能力層次不同的學生，采取以下教學策略：(1)以幾何發展史為經、以數學思想為緯，引領學生穿越時空，對話大師，體驗數學文化，浸潤科學精神；(2)通過講述數學奇聞軼事、將數學與生活類比等方法激發學生的學習興趣，降低認知負荷，理解公理化思想與真理的相對性；(3)賞析精選案例，力求兼顧不同層次，內容上既要能自然銜接，下通初中數學，又要能高屋建瓴，上通高等數學；(4)課堂教學重點應放在普適性內容上，同時要留有數學思考和拓展閱讀的空間.

2.4 教學過程設計

·對話歐幾里得，初識幾何原本

軼事兩則(1)托勒密國王向歐幾里得求教學習幾何學的捷徑，歐幾里得答道：“幾何無王者之道.”(2)一名學生初學幾何學第一個命題，就問歐幾里得學了幾何將得到什么.歐幾里得對身邊侍從說：“給他三個錢幣，因為他想在學習中獲取實利.”

閱讀思考自主閱讀《幾何原本》相關內容材料，學生代表發言概述主要內容，其他學生補充，最后進行師生小結.

設計意圖其一，以饒有趣味的“軼事兩則”引發學生興趣，引導學生閱讀相關材料；其二，“幾何無王者之道”滲透學科德育，勉勵學生不圖捷徑，努力求學；其三，“學了幾何能得到什么”初步展示古希臘數學不重實利的特點，為下文中西數學比較作了必要鋪墊；其四，“閱讀思考”旨在引導學生學會數學地閱讀與思考，從而獲取知識，發展能力.

·體悟公理思想，比較中西數學

問題研討1嘗試用自己的語言闡述對公理化思想的理解以及《幾何原本》的歷史價值.

問題小結《幾何原本》不僅僅是幾何教科書，也構成了歷史上第一個數學公理體系，被視為嚴密科學思維的典范，對西方數學、科學和文化產生了不可磨滅的重大影響.

素材1 (道生萬物)《道德經》開篇有言：“道生一，一生二，二生三，三生萬物.”從數學的視角來看有何啟示？

素材2 (數學瑰寶)簡要介紹《九章算術》，并附以書中問題兩例(內容略).

設計意圖“道生萬物”具有濃厚的中國傳統文化色彩，充滿思辨卻少形式邏輯.《九章算術》作為不朽的數學瑰寶，是中華傳統文化的杰出代表，特色顯著.通過這些素材幫助學生確立對中國古代數學的基本認知，進而樹立文化自信，同時順勢提出中西數學比較的問題.

問題研討2嘗試基于文化視角比較中西數學的特色.

問題小結中國古代社會實行君王統治，強調“經世致用”，數學研究主要出于實用目的，逐步形成算法特色.西方社會實行“民主政治”，崇尚理性精神，重視邏輯推演.中西數學各有特色，我們不必妄自菲薄，但也要認清不足，揚長補短，爭取早日實現數學強國之夢.

·論戰非歐幾何，領略大師風采

歐氏幾何的“家丑”：《幾何原本》并非完美無瑕，尤其是第五公設引發了極大的爭論，許多數學家試圖從其他公理、公設中把它推導出來，結果都以失敗而告終.

非歐幾何的誕生：1826年，羅巴切夫斯基用“同一平面上任何兩條直線都不相交”代替第五公設，標志著非歐幾何的誕生.研究成果公布后，羅巴切夫斯基飽受嘲諷和攻擊，但他仍堅持研究和發展非歐幾何，堪稱“幾何學的哥白尼”.

設計意圖課程實施時不要拘泥于非歐幾何知識本身，而應突出以下兩點：一是轉變數學公理永恒不變的片面認知，二是勉勵學生以羅巴切夫斯基為榜樣，無論是現在求學還是將來做學問，要敢于質疑和挑戰權威，勇于追求和捍衛真理.

·追問絕對真理，求索知識大道

問題研討3談談你對數學真理性的認識.

問題小結(1)真理的相對性.人們長期將數學視為絕對真理.非歐幾何的創立，在一定程度上標志著數學真理性的終結.數學家可以建構公理體系，具備極大的創造自由.每一個學生都可以成為數學的探險家、發現者.(2)棋類游戲的隱喻.同樣的網格紙與黑白棋子，可以下圍棋，也可以下五子棋.雖然可以根據興趣愛好確定游戲規則，但能否吸引人去玩，卻需要實踐來檢驗.因此，公理體系要能反映人類的需求和愿望，數學來源于實踐，服務于生活.

課堂小結幾何學因土地測量而產生，是研究形的科學，其發展首先是堪稱思維典范的歐式幾何，爾后又有顛覆傳統的非歐幾何，這兩種幾何的誕生不僅對數學發展產生了不可估量的影響，同時也對科學和文化的發展產生了重大影響.

作業布置本節課的作業分為必做作業和選做作業.

(1)必做作業：參考以下選題，收集幾何學的相關資料，撰寫一篇心得或論文.

①幾何學的發展史及其感悟；②中國古代數學家的幾何學貢獻；③中西幾何特色比較——以《九章算術》和《幾何原本》為例；④非歐幾何的科學價值與思維啟迪；⑤數學改變生活——例談幾何學的應用.

(2)選做作業：開展小組合作，制作多媒體課件或板報等，并在課堂或校園內進行交流展示.

設計意圖必做作業要求全員參與，分為兩個層次：基本要求是寫一篇字數不多的學習心得；提高要求是查閱資料并撰寫論文(可作為數學文化課程的期末論文)；選做作業側重個性發展，旨在為學生提供發揮特長、展示自我的舞臺.

課后，聽課教師從三個維度對本節課進行了評價.從教學目標來看，能立足學情，以數學史為載體，做到文理綜融，貫通中西，注重弘揚數學精神，滋養人文素養；從教學內容來看，注重初高中銜接，適度對接高等數學，深入淺出，雅俗共賞；從教學效果來看，學生積極參與，思考有深度，在交流中不斷碰撞出思維火花.

3 結語

總體來看，高中“數學文化”課程的開發與實踐活動，仍然處于起步階段，缺乏可供參考的系統化成果，優秀的課程資源和教學案例不多且零散.[10]為增強課程實施效果，首先要牢記“文化育人”的理念定位，融通文理，著力將數學文化的學術形態轉化為教學形態；其次要樹立精品意識，扎根實踐，長期耕耘，積累數學文化素材，打磨優秀課例進而形成系統化課程.如此，數學文化必能成為提升數學素養、實現融合育人的重要支點.