探索例題教學,深化思維過程

[摘? 要] 數學教學中教師常常采用例題教學讓學生實現舉一反三的能力，并滲透數學思想方法，以達到提升思維能力的目的. 例題教學不能停留于當前問題的解決，應該從一道題的解決推廣到一類題的解決，使學生真正收獲數學思維和思想.

[關鍵詞] 例題教學;思維過程;舉一反三

作者簡介：鐘淑民（1967—），本科學歷，中學一級教師，從事初中數學教學與研究工作.

數學知識的學習中常常會用到“舉例說明”的方法，即教師以例題進行教學引導學生學習一種解題方法或者某一知識點，因此這一教學方法的第一要務是提升學生運用新知解決問題的能力，加深學生對新知的理解，學習運用新知的技能，但是“舉例說明”的方法如果止步于此，是遠遠不行的，這只是例題教學的初級階段.

數學學習還要求學生能夠“舉一反三”，通過教師的例題教學“舉一”，運用方法獨立解決問題實現“反三”. 因此教師挑選例題時應該選擇具有典型性和較大擴展空間的習題，才能更好地實現學生“舉一反三”. 下面筆者通過教學實踐談一談如何更好地進行例題教學，與各位同行交流.

優化例題教學過程，提升思維能力

在一次復習課中，筆者提出了一道非常典型的試題，現在將教學過程實錄如下：

例1? 直線a的一側有兩個定點A和B，如何在直線a上確定一點P，使得PA+PB最小？

（這個問題使學生紛紛陷入了思考）

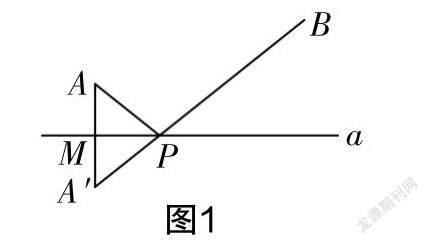
生1：我想起來了，老師講過這種題. 只要作直線a的垂線AM，垂足為M，再將AM延長到A′，使得AM與MA′相等，將A′B連接起來，那么線段A′B和直線a的交點就是我們要求的點P！（生1一邊說一邊演示，如圖1所示）

這時其他學生慢慢想了起來，七嘴八舌地說：“哎呀，老師講過，我怎么忘了呢！”

（此時筆者繼續追問）

師：為什么這樣做能使PA+PB最小呢？

生（異口同聲）：因為兩點之間線段最短.

師：為什么A′B的長最短，PA+PB就最小呢？

（學生開始竊竊私語，然后提到：根據證明可以得到PA與PA′相等，所以PA與PB的和等于A′B，如果A′B的長最短，那么PA+PB就最小）

師：那我們再思考一下，點P是唯一的嗎？怎么才能證明直線a上的其他點不能滿足這個條件呢？

（這時學生面露難色，他們沒有想過這個問題）

本題雖然難度不高，但是設計精巧，內涵豐富，它具有在實際問題中構建數學模型的參考價值，同時含有對稱變換思想方法的應用，還蘊含著幾何中對“最值”問題的邏輯論證思路……這些內容是這道例題值得渲染的亮點，也是選擇和講解這道例題的內在價值.

因此，在本題的教學過程中，教師除了要讓學生知道解法外，還要讓學生體驗數學思想方法的應用，從而提升思維能力，將這一解法在其他試題中進行推廣，學會知識的遷移和運用，這才是解決這道例題的深層次的目的[1].

在教學過程中，教師還可以通過設置“問題串”的方式，引導學生參與問題解法的探究討論，實現認識的升華.

優化教學過程：

師：這道題的目標是解決線段“最短”，那么在你學過的哪些幾何知識中，見過“最短”的結論？又是怎樣論述的呢？

生2：我們學過“兩點之間線段最短”這個結論，還有一個結論是“直線外的點與這條直線上所有點之間的線段，垂線段最短”.

師：很好，這道題研究的也是“最短”，那么與你提到的這兩個定理有什么區別？

生2：題目中的“最短”是兩條線段的和，即一條折線段的最短，這是不一樣的.

師：很好，這就是我們需要解決的問題. 我們知道，點A與點B之間最短的距離是線段AB的長，但是這與直線a上的點P是無關的，讓我們無法找到解決問題的方法. 現在我們能否將問題分解一下，來推動問題解決呢？

生3：假設將點A移動到直線a的另外一邊，那么線段AB與直線a就有了交點，這樣是不是就有點P了……

師：很好！但是要怎樣移動點A？要移動到直線a另外一邊的哪里呢？

（學生開展集體討論，紛紛發表自己的意見）

生4：作線段AA′與直線a垂直，垂足為M，并且使AM與MA′相等，通過證明△AMP與△A′MP全等，得到線段AP與A′P相等.

師：講得太好了，這樣就知道AP與PB的和等于A′P與PB的和，問題就轉化成了A′P+PB何時是最小的.

生5：我們連接點B和點A′，與直線a的交點就是問題所求的點P！

師：這樣我們似乎找到了正確的解法，但還有一個問題沒有解決，點P是唯一的嗎？怎樣才能證明直線a上的其他點不能滿足A′P+PB最小？

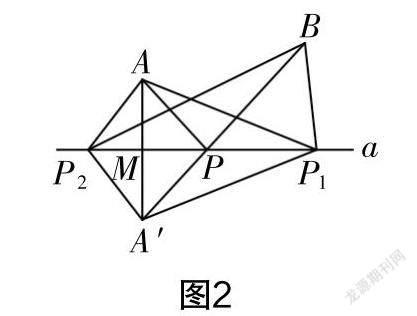
生6：如圖2所示，假設直線a上有點P和點P，我們可以用一樣的方法證明AP與A′P相等，AP與A′P相等. 通過三角形三條邊的關系可以證明AP+BP，AP+BP都大于AP+PB.

師：看來我們只需要證明直線a上不是點P的任意一點相應的兩條線段之和都大于AP與PB的和，就能夠說明只有唯一的點P可以使AP+PB最小.

通過這樣的方法，學生不僅學會并理解了本題的解法，而且通過親身體驗探究，以及參與尋找解題方法的探索過程，掌握了解題分析和思考的方法，初步認識了推理“最值”的邏輯方法，這些都為實現“舉一反三”打下了堅實的基礎[2].

強化例題解法理解，提升“舉一反三”的能力

解決幾何問題時經常需要添加輔助線，變換圖形后再解決. 添加輔助線可使圖形的位置移動，而圖形的角、線段等大小不變或者按比例發生變化，它能促進問題得以解決，這樣能使學生對輔助線的認識更加清晰，提高其解決幾何問題的能力.

上述問題的解決過程中，學生認識到通過作線段AA′與直線a垂直（垂足為M），使得線段AM與MA′相等，這一輔助線構造了全等三角形，實際上是為了找到點A的對稱點A′. 要探究“最小”的問題，當點A移動的同時，點P也會在直線上移動，需要保持AP與A′P相等. 因此，通過作輔助線進行圖形變換，從更高層次的思維上來說是構造全等的或者成比例的線段.

教學中教師要提高學生作輔助線變換圖形的能力，首先要培養學生對輔助線和圖形的敏感度，增強學生認識和理解各類輔助線的意義，以及圖形變換的意義和作用. 同時，教學中教師要通過例題講解，引導學生以多種角度運用知識，進一步夯實對知識的理解，加深印象. 例如，筆者通過上述例題講解示范后，列舉習題進行檢測，能考查學生對知識的掌握程度.

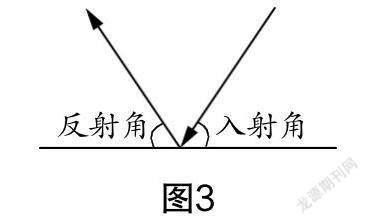
例2? 桌球在桌面上滾動時，碰到臺邊會改變方向，向另一個方向沿著直線繼續運動，由此可以知道它的變化規律：入射角與反射角相等. （如圖3所示）

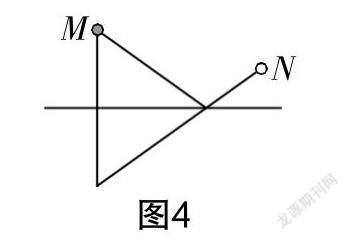
（1）如圖4所示，桌球臺內有一個位于點N處的白球和一個位于點M處的紅球，請問將白球往桌球臺邊哪點撞擊，可以通過反彈擊中紅球？

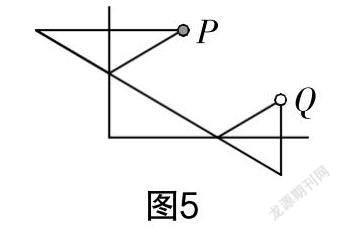
（2）如圖5所示，桌球臺內有一個位于點P處的紅球和一個位于點Q處的白球，請問將白球向桌球臺邊哪點撞擊，通過兩次反彈可以擊中紅球？

列舉例2的目的是讓學生進一步理解和體驗例1中的思想方法的運用，體驗圖形轉換對解決問題的關鍵作用，使學生形成解決類似問題的重要思想策略.

例2與例1具有相同的性質和解決思路，學生能夠仿照例1很快獲得解決例2的路徑，從而激發學習興趣，增強學習數學的信心. 筆者發揮了教師應有的主導作用，組織學生探究和辨析解題方法，使學生能夠根據入射角與反射角相等的原理，從第（1）問聯想到軸對稱變換，從第（2）問提升思維深度產生更加靈活的變化，學生在這一問中找到了解題方法，收獲了成功的喜悅，激發了學習興趣[3].

為了提升學生“舉一反三”的能力，筆者加入了變式練習，讓學生運用例1的解法去解決與例1的表象相距較遠的問題.

例3? ∠AOB的邊OB上有一個定點P，請在∠AOB的邊OA上求一點Q和邊OB上求一點R，使得PQ+QR最小.

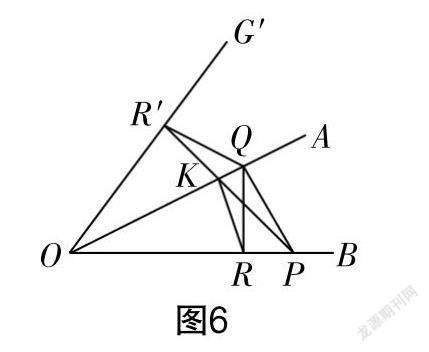
（1）如圖6所示，根據定理“直線外的定點與直線上所有點連接的線段中，垂線段最短”，可得點P到OA的最短距離是垂線段PQ的長，同理點Q到OB的最短距離是垂線段QR的長，此時PQ+QR最小. 以上說法正確嗎？請說一說你的理由.

師：我們學過有關距離“最短”的定理，但是沒有定理能夠保證最小值的和一定也是最小值，因此上面的說法需要我們進行研究. 根據解答例1的經驗，研究折線段的長最短的問題，需要我們將折線段向直線段靠攏，再進行比較. 因此，我們作以OA為軸的軸對稱變換，得到射線OG′和點R的對稱點R′，可知QR與QR′相等，這樣PQ+QR等于PQ+QR′（如圖6所示）. 同學們，仔細觀察一下，你發現了什么？

生7：我發現，連接PR′，它與OA相交于點K，可以得到PK與KR的和等于PK與KR′的和（PR′），因為PR′小于PQ與QR′的和即PQ與QR的和，所以PQ+QR不是最小的.

師：你說得太精彩了，這樣我們就證明了“最小值的和等于和的最小值”這個說法是不對的，同時也告訴我們數學猜想需要通過證明才能作為推理論證的依據.

（2）請你正確解答例3，并驗證你的答案.

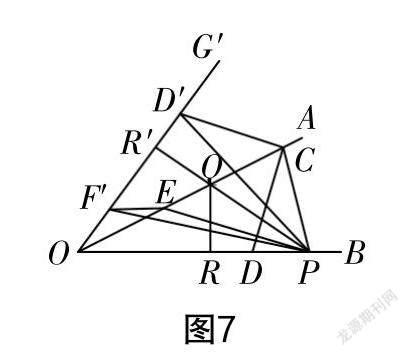
生8：在研究第（1）問的基礎上，我們知道了經過對稱變換后，原來的折線轉化為了點P與射線OA、射線OG′上的點連起來的折線，如圖8中的折線PEF′，PCD′，它們的長大于PF′，PD′的長，并且大于垂線段PR′的長. 設PR′與OA相交于點Q，點R與點R′關于OA對稱，此時R使得PQ+QR最小，是我們要求的目標.

探究例3，是對例1的解法的深層次擴展，加深了學生對數學思想方法的認識，拓寬了學生的視野，奠定了學生在更加廣闊的范圍里使用這一思想方法的基礎.

下面筆者繼續安排例題發展這種解題能力，提高學生對移動圖形的規劃能力和變化方式的選擇能力，以及學生靈活解題的能力.

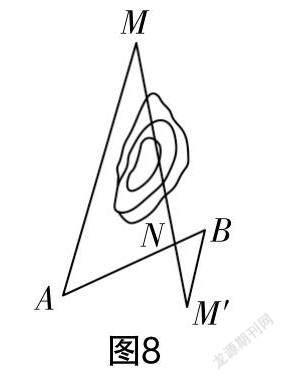
例4? 如圖8所示，從觀測站A觀測到北偏東方向有采油豎井M，距離為3.6千米，在采油豎井M的南面山丘后有一油罐車轉運站N，它與觀測站A的距離為1.2千米. 現要從轉運站N處修一條輸油管道到采油豎井M，但由于中間隔著山丘而無法直接測量距離和方向，請你設計一種方案，確定輸油管道的長和方向.

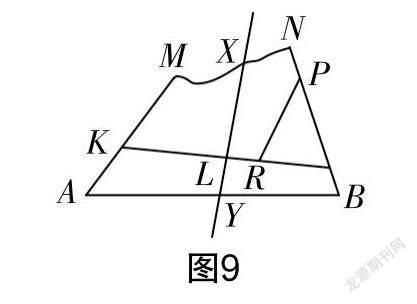
例5? 如圖9所示，有一張三角形紙ABC，角C已經被撕掉了，怎樣才能作出角C的平分線呢？請你想一想有哪些作法，并進行證明.

上述例4和例5屬于同一類問題，解答目標較為隱蔽，通過圖形變換使隱性的問題轉變為顯性的問題是解題的必然路徑，教師除了要引導學生用軸對稱方法外，還要幫助學生學會通過中心旋轉和大小放縮等方法進行圖形變換.

通過這些問題的分析和解決，學生能夠實現從例1到例5的解題經驗和知識的遷移，并根據具體的情況利用圖形變換解決更多問題.

教學反思

例題教學的目標是通過一道題培養學生“舉一反三”的能力，因此教學中教師要挖掘解題背后的思想方法和策略背景，讓學生真正掌握一道題甚至一類題的本質，體會數學的精髓. 要提高例題教學的實效性，筆者認為需要關注以下幾點：

（1）精選例題. 例題教學的關鍵是挑選典型和內涵豐富的習題作為例題，通過例題教學使學生掌握數學解題中經典的思想方法，對于知識的遷移具有較大的空間.

（2）精選系列例題. 例題教學并不是以解決一道題作為終點，而是要精心準備系列例題與典型例題相互呼應，鞏固和拓展知識，為學生的知識運用打下基礎.

（3）體驗探究過程. 教師要積極組織學生探索例題解法，總結解題規律，體驗數學思想和方法的應用，增強學生學習的信心，激發其學習興趣.

（4）注重解題層次. 在例題研究時教師要層層遞進、循序漸進，從與典型例題“形似”的例題開始拓展，到“神似”例題的研究，提高學生的解題能力，夯實知識基礎.

（5）課后鞏固. 教師還要準備相應的課后鞏固訓練，以實現訓練的閉環，加深學生對知識的印象.

總之，例題教學要著眼于學生的長遠發展，在例題中滲透數學思想方法，實現“舉一反三”.

參考文獻：

[1]候學萍，朱亞麗. 初中生數學自主學習能力研究[J]. 教學與管理，2019（18）：29-32.

[2]宋子紅. 初中數學復習課教學策略研究[D]. 華中師范大學，2019.

[3]劉岳，康翠. 初中數學簡約課堂教學的探索與實踐[J]. 教學與管理，2015（25）：41-44.