遺傳蟻群混合算法在高職院校排課系統中的應用

李印坤?任宣宇

摘要：排課是高職院校的日常工作，排課管理是否合理，直接影響了高職院校的辦學質量。基于此，將遺傳蟻群混合算法作為研究工具，針對高職院校排課管理系統進行優化研究。將混合遺傳螞蟻算法應用于高職院校排課系統中，利用交叉函數設計和構建了高校自動排課系統。選擇某高職院校的課程調度系統進行研究，利用遺傳螞蟻混合算法對原系統A進行改進，形成一個新的系統B，比較兩個系統的運行時間和系統適應性。實驗結果表明，系統B的適應度優于系統A，遺傳蟻群混合算法可以提高課程的合理性。

關鍵詞：遺傳蟻群混合算法；排課系統；高職院校

一、前言

近年來，隨著我國高職院校規模迅速擴大，許多高職院校都面臨著課堂資源和教師資源不足的問題，組織課程的方式越來越難以滿足不斷變化的需求。排課問題一直困擾著很多高職院校，特別是班級較多而教學資源緊張的學校，每次排課都是困難重重，在實際工作中，許多學校只能無奈地選擇手工排課。實現全自動化的排課系統是眾多高職院校的共同期待。

排課問題是NP中的時間表問題，也就是在資源條件有限的情況下，將事件安排到適合的時間段。問題的核心在于為學院計劃制定合理的課程安排，包括分配教室、時間和教師資源，并確定適當的教學時段和場地，以便有序地進行教學工作，進而設計一個滿足多約束條件且高效運行的智能排課系統[1]。

國外學者解決排課問題大多采用智能算法，比如IA Ashari采用結合遺傳算法和蟻群算法，以優化解決排課問題。經過實驗和大量測試，證明遺傳算法在此問題中表現良好[2]。G. Kendall及其團隊將禁忌搜索算法與模擬退火算法相結合，提高可行解質量，并成功求解排課問題[3]。Saptarini等學者應用遺傳算法有效地避免了違反硬約束條件，在最大限度上滿足軟約束條件[4]。C.Akka等研究人員將遺傳算法和模擬退火算法相結合，適應排課規模的變化，并應用于排課系統中[5]。

但國外的排課系統普遍不適用于我國高校。袁俊毅設計了一種基于遺傳算法的排課系統，成功應用于高職院校，顯著提升了排課效率[6]。羅義強等學者采用改進的粒子群算法優化高校排課問題，通過該算法得到潛在解并驗證其有效性。馮月華則運用動態調整信息素策略改進蟻群算法，并將其應用于排課系統中，成功縮短了排課時間。

為了提高高職院校的排課效率，本文提出一種將遺傳算法與蟻群算法混合使用的方法，通過遺傳算法對初始種群進行優化選擇，進而生成蟻群算法所需的信息素，再通過蟻群算法求得全局最優解。本文選擇某高職院校的一個教務管理系統進行實驗研究，將原有的系統與運用混合算法改進后的系統進行比較，通過比較遺傳蟻群混合算法的運算時間和適用性，發現該算法可以更好地提高高職院校排課的合理性。

二、高職院校的排課特點

根據教育分類的觀點，高職教育不屬于普通高等教育，而是技術與職業教育中的高等教育。2022年修訂的新《中華人民共和國職業教育法》第三條闡明“職業教育是與普通教育具有同等重要地位的教育類型”。特殊的教育類型決定高職院校的排課工作也具有挑戰性，既有普通高等學校排課的復雜性，又有自身的特殊性。

1.高職院校的特點之一是教學資源比較緊張，除了一般的教室、機房、實訓室、體育場地，教師資源緊張也是高職院校在排課方面遇到困難的共同點，很多高職院校的教師周課時為18節至20節。

2.一般全院的課程表就是公共基礎課的安排，專業課程由各系安排。排課中最大的挑戰在于公共選修課。不同專業或班級的學生可能會選擇相同的課程，而各門選修課人數也參差不齊，因此安排教室變得十分困難。

3.受到教師資源限制，很多高職院校采用兩個及兩個以上的班級合堂上課，需要使用合堂教室或階梯教室，而合堂教室或階梯教室需求量較大又會帶來諸多相關的問題。

4.部分高職院校采取單雙周上課模式，或者分階段安排實訓課，課程表的分階段變化在一定程度上增加了排課的復雜性。

三、高職院校排課問題分析

基于高職院校的排課特點，排課問題主要涉及課程、班級、教師、教室、上課時間等因素，排課的實質是課程表中不能在上面5個因素之間發生沖突。為描述問題方面，下面使用5個集合表示這些因素。

（一）硬約束條件

在高職院校排課過程中，硬約束條件是必須遵守的限制條件。如果硬約束條件無法滿足，則無法得到最優解，進而導致教學計劃無法實施。根據高職院校的排課特點，具體硬約束條件有以下幾點：

（二）軟約束條件

軟約束條件是指那些是否滿足都不影響教學計劃實施，但影響師生體驗的約束條件。為了提高師生對課表的滿意度，在排課的同時要充分考慮人體生物規律。在排課的過程中，滿足軟約束條件越多，教學計劃實施起來越順利，課表也越能讓師生滿意。

例如：①盡量將難度較大的課程或對思維訓練要求較高的課程安排在上午第1、2節課等節次，在這些時間段學生思維相對更活躍；②體育與健康課程盡量安排在上午的第3、4節和下午的第5、6節，充分考慮到體育鍛煉后因身體疲憊，不適宜立刻進入專業性過強的課程。

四、遺傳蟻群混合算法

（一）遺傳蟻群混合算法的基本思想

通過對參考文獻的研究發現，在解決高校排課問題時，遺傳算法和蟻群算法各自具有一定的優勢，但也存在相應的缺陷。例如，在尋求最優解的初始階段，遺傳算法的搜索效率較高，適用于大范圍的搜索。但在尋求最優解的后半階段，遺傳算法沒有充分利用反饋信息，這一不足之處就會顯現出來，并消耗大量的時間在無效的迭代上。突出的并行計算能力和整體優化能力是蟻群算法的最大優勢，但不足之處是，在算法初期，信息素的匱乏會導致尋求最優解的速度過慢，因而該算法的運行時間比較長。

針對高職院校的排課特點，本文在前人研究的基礎上進一步將遺傳算法和蟻群算法結合起來使用，可以更好地發揮它們各自的優勢。具體而言，在算法運行過程中，可以先充分利用遺傳算法的優點，以期達到更高的搜索效率。即在初始階段具有高效搜索的特點，進而能夠生成必要的信息素，以供接下來蟻群算法的使用，然后利用蟻群算法求得全局最優解，充分利用了蟻群算法的整體優化能力和突出的并行計算的能力。

（二）遺傳蟻群混合算法的執行步驟

遺傳蟻群混合算法的執行步驟如下：

Step 1 初始化遺傳算法的參數，生成初始種群，并將初始迭代次數設為0；

Step 2 計算所有個體的適應度函數；

Step 3 對個體進行基本遺傳操作，迭代次數加1；

Step 4判斷是否滿足終止條件，如果滿足，繼續執行，否則跳至Step 2；

Step 5 利用遺傳算法尋求近似最優解，并將其轉化為初始信息素，以供蟻群算法使用，然后構建排課問題的二分圖模型；

Step 6 在蟻群算法運行前，初始化相關參數，并將迭代次數設置為gen=0；

Step 7 將m只螞蟻放GLSC（在二分圖左側的頂點集）中，為每只螞蟻建立禁忌表tabuk和允許RTR選擇的表allowdk；

Step 8 螞蟻k根據排課約束條件和轉移概率選取轉移路徑；

Step 9 對m條路徑進行記錄，并完成迭代；

Step 10 計算m條路徑的長度，并對當前最優路徑值進行記錄；

Step 11 對最優路徑上邊的信息素量進行更新，揮發其余邊的信息素；

Step 12 判斷是否符合終止約束條件，若符合，則終止運算，求出當前最優路徑的數值，否則gen=gen+1，并返回Step 7繼續新的迭代。

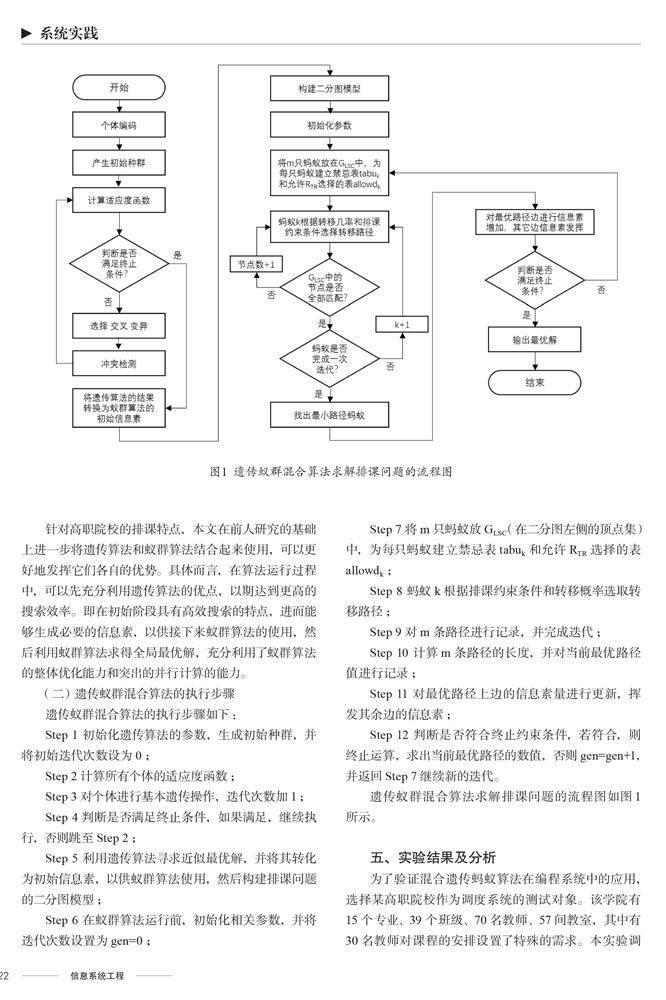
遺傳蟻群混合算法求解排課問題的流程圖如圖1所示。

五、實驗結果及分析

為了驗證混合遺傳螞蟻算法在編程系統中的應用，選擇某高職院校作為調度系統的測試對象。該學院有15個專業、39個班級、70名教師、57間教室，其中有30名教師對課程的安排設置了特殊的需求。本實驗調度系統采用較為常用的蟻群算法，在本文研究的基礎上，刪除原算法，代之以遺傳螞蟻混合算法。利用上述實驗數據，我們分別在蟻群算法和遺傳蟻群混合算法中進行多次實驗。我們將原有的蟻群算法系統簡稱為A系統，對于遺傳蟻群混合算法則稱之為B系統，并對兩種算法解決排課問題的合理性、效率等方面進行驗證。

（一）算法運算時間比較

當排課單元為100、400、800時，對A系統和B系統的運行時間以及適應度進行比較，并進行詳細分析。算法運算時間比較如表1所示。

表1中的數據顯示系統A比系統B所花費的操作時間更少。當調度單元為100時，系統A為56，系統B為36；當調度單元為400時，系統A為192，系統B為174；當調度單元為800時，系統A為578，系統B為541。

算法運算理想的時間長度是衡量算法質量的一個重要關鍵績效指標。運算時間越短，可能的損失就越小，帶來的機會就越多。通過表1可以發現，隨著排課單元數量的增加，兩種算法的運行時間也會隨之增加。在排課單元數量相同的情況下，蟻群算法所需時間較長，而遺傳蟻群混合算法則需要較短的時間。

（二）算法適應度比較

在遺傳算法中，適應度是描述遺傳算法個體性能和驅動力的主要指標。從生物學的角度來看，正常的條件相當于“適者生存”的生物可持續性競爭，這在遺傳過程中很重要。建立優化問題的目標操作與個體適應性之間的映射關系，有助于實現優化問題在群體發展中的客觀作用。因此，我們比較兩個系統的適應性，結果如表2所示。

從表2的數據可以看出，系統B的適應性優于系統A。當調度單元為100時，系統A為191，系統B為213。當調度單元為400時，系統B比系統A高31。當調度單元為800時，系統B比系統A高69。可以看出，隨著排課單元的增加，兩種算法的適應度值也在增加。隨著排課單元數量的增加，兩種算法的適應度值都會趨于穩定。因此可以得出結論：在相同數量的排課單元下，遺傳蟻群混合算法的適應度要優于單一的蟻群算法。

六、結語

綜上所述，遺傳蟻群混合算法的排課時間比蟻群算法短，而且其適應度值遠大于蟻群算法，因此，運用遺傳蟻群混合算法解決排課問題的可行性已經得到驗證。將蟻群算法與遺傳算法相結合，首先采用蟻群算法隨機搜索，具有良好的全局收斂性，然后充分利用并行性，對前向反應機制和有效性進行了高層次的分析，建立了一種高層次分析的有效遺傳算法。采用遺傳蟻群混合算法可以有效提高算法的收斂速度，縮小搜索范圍。實驗結果表明，遺傳蟻群混合算法顯著提高了高職院校課程設計系統的效率和合理性。該算法生成的課程規劃方案在每門課程中均勻分布，基本滿足高職院校的要求。

參考文獻

[1]孫弋，胡粔琿.基于遺傳——蟻群混合算法的排課系統[J].計算機系統應用，2019，28（2）：81-86.

[2]Ashari IA，Muslim MA，Alamsyah A.Comparison Performance of Genetic Algorithm and Ant Colony Optimization in Course Scheduling Optimizing[J].Scientific Journal of Informatics，2016，3（2）：51-60.

[3]Goh SL，Kendall G，Sabar NR.Improved local search approaches to solve the post Enrolment course timetabling problem[J].European Journal of Operational Research，2017，261（1）：17-29.

[4]Saptarini NGAPH，Suasnawa IW，Ciptayani PI.Senior high school course scheduling using genetic algorithm[C].2018.

[5]Akkan C，Gulcu A.A bi-criteria hybrid Genetic Algorithm with robustness objective for the course timetabling problem[J].Computers & Operations Research，2018，90：22-32.

[6]袁俊毅.基于遺傳算法的高校教務排課系統設計與實現[D].長沙：湖南大學，2017.

作者單位：煙臺文化旅游職業學院