關于新課標下初中數學作業優化設計的深思
蔣波

【摘要】在任何教育階段的任何學科教學中,除新授知識,都有作業設計這一環節,主要目的在于幫助學生鞏固新學知識,使其發現不足之處,讓學生有針對性地查漏補缺.在新課標下的初中數學教學中,作業設計屬于教學活動的關鍵構成部分,作業設計質量的高低影響學生的最終學習效果,教師要以新課標為導向重新優化設計,提高學生的學習效率.本文主要關于新課標下初中數學作業的優化設計進行深思,并分析一些個人建議.
【關鍵詞】 新課標;初中數學;作業設計
作業指的是為完成學習方面的既定任務而進行的一類活動,有書面、口頭、實踐等多種形式,主要分為課堂作業和課外作業兩大類,無論是哪種形式的作業,其質量、效果如何,都會直接影響到整體教學情況.在新課標下的初中數學教學中,教師應科學優化作業設計,利用合理、恰當的數學作業助推學生深化理解與記憶課堂所學的理論知識,使其能夠慢慢地把數學知識轉變成能力與技巧,掌握正確的解題竅門,讓他們體會數學思想方法的作用.
1 設計形式多變作業,調動學生參與熱情
現階段,隨著多媒體技術、網絡技術、信息技術等相關教育手段的持續更新與發展,已經廣泛運用至各個教育階段、各科教學的各節課教學之中,自然也包括初中數學課堂,這是創新課堂教學形式的有效途徑之一,對提升整體教學質量有著舉足輕重的作用.在新課標下的初中數學作業設計環節,教師同樣可以借助現代教育技術的優勢,善于設計一系列形式多變的數學作業,極力引發學生完成作業的動力與熱情,使其全身心地參與到作業完成中[1].
例如 在開展“余角 補角 對頂角”教學時,教師布置作業時,可以利用網絡手段設置朋友圈或者好友群,把相關數學作業分享到里面.
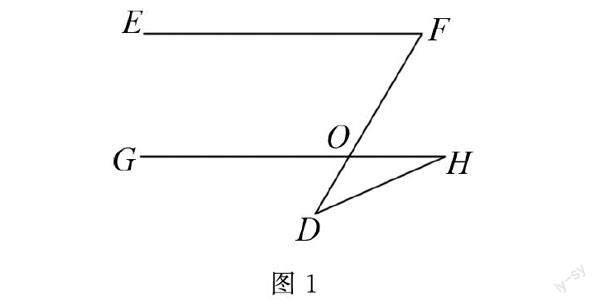
在圖1中,EF與GH是平行關系,其中∠F的大小是56°,求∠H與∠D的度數之和.
解析:要想求出∠H與∠D的度數之和,就需要找出∠H、∠D與∠F之間的關系,因為∠GOD=∠H+∠D,所以能夠利用平行當作媒介輕松解答這一問題.
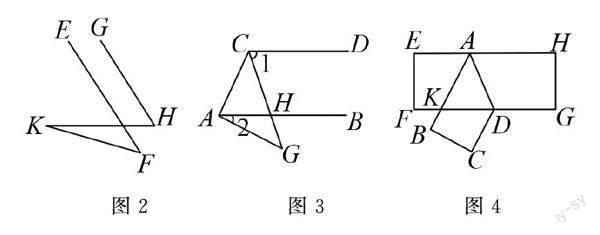
因為該知識點在數學題目中有著廣泛運用,教師可以設計以下變式訓練:(1)如圖2所示,EF與GH是平行關系,其中∠H=52°,∠HKF=20°,求∠F的大小;(2)如圖3所示,AB與CD是平行關系,∠1=3∠2,∠2=28°,求∠G的大小;(3)如圖4所示,將一個長方形硬紙板EFGH沿著AD進行折疊,如果∠ADK=50°,求∠AKD的大小.
這樣利用一題多變帶給學生新穎、個性的作業,使其對數學作業充滿興趣與期待,他們完成后主動分享答案,并結合學生的速度和準確度給予相應的表揚,讓他們在后續作業中表現得更為積極.
4 設計開放數學作業,拓展學生思維空間
在新課標下的初中數學教學實踐中,常規教學范圍已經不再僅僅局限于固有的教材與配套輔導資料,大力倡導開放性教學空間的營造,這不僅需體現在新知識的講授方面,還要在作業設計上有所呈現,積極打造開放式課堂,推動整體教學質量的改善.因此,初中數學教師應當以新課程標準為基本導向,結合所授內容設計一系列開放性的數學作業,引領學生從不同視角思考問題,使其全方位的分析與研究題目內容,切實提升他們的數學思維水平[4].
例如 以“多項式的因式分解”教學為例,完成基本教學任務以后,教師先設計一些常規化的作業,如:x2-xy,x2+xy,x2-y2,x2+y2,以上多項式中能夠使用公式法來分解因式的有哪些?如果a+b的值是4,那么a2+2ab+b2的值是什么?因式分解(x-1)2-9的結果是什么?李軍抄某個分解因式題目時,不小心把x的指數漏抄掉,他只知道該數是一個不大于10的正整數,還可以使用平方差公式進行因式分解,他抄在作業本上的式子是xΔ-4y2(“Δ”表示漏抄的指數),那么該指數可能是什么?以此幫助學生鞏固有關因式分解的基礎知識.接著,教師可設計開放性作業,讓學生兩人一組,分別給對方設計關于因式分解的題目,要涉及平方差公式、公式法的應用,使其充分調動個人主觀能動性優化題目內容,驅使他們感受到數學作業的樂趣.這樣既有助于學生進一步了解因式分解的結構特性,還強化他們完成數學作業的積極性,使其思維得以發散,促進創新思維的生成.
5 設計多樣數學作業,注重學生全面發展
尊重初中生的多樣性和個性化作為新課標下初中數學教學中的基本教育理念,還是提升數學作業設計有效性的核心理念,這關系到他們的整體學習質量.因為初中生在數學知識水平、認知能力、生活經驗、學習需求等方面有著明顯的不同,教師設計數學作業時應當突出多樣性,除傳統的書面紙質作業外,還要布置一些口頭、動手操作與生活調查類的作業,以此滿足不同學生學習數學知識的需求,使其都有心儀的作業可做,升華他們的學習效果[5].
例如 在“平面直角坐標系”教學過程中,學習完成新課內容以后,教師可以設計以下兩個作業:(1)在某個平面直角坐標系之中,請找出如下各個點的位置,A(-4,3),B(4,-3),C(2,0),D(0,2),E(6,1),F(6,2);在一個平面直角坐標系之中,嘗試標出以下各點,其中M點位于x軸上面,且同原點之間的距離是2個單位長度,N點位于y軸上面,且同原點之間的距離是4個單位長度,P點位于第一象限,同x軸的距離是5個單位長度,同y軸的距離是2個單位長度,Q點位于第二象限,同x軸的距離是1個單位長度,同y軸的距離是4個單位長度.從表面上來看,這兩道數學作業從本質上均是考查學生對平面直角坐標系的理解和認識情況,不過這兩道題目的出發點又有所不同,他們在做作業過程中將會產生不一樣的情感體驗,既能夠滿足初中生多樣化的學習需求和情感體驗,還可以現在提升作業的布置效果,使其獲得全面發展.
6 結語
總而言之,在新課標下的初中數學教學活動中,教師需重新審視作業的布置與優化設計,結合具體教學內容、數學知識特征及初中生的身心特點創新作業內容和形式,突出作業的多變性、適配性、層次性、開放性、多樣性與實踐性,帶給他們豐富多彩的數學作業,增強完成作業的興趣、動力與熱情,真正發揮出作業應有的功能及價值,使其有所收獲與成長.
【本文系江蘇省宜興市學科微課題2022年度好課堂專項課題(項目編號:YW-h/2022/026)“新課標背景下初中數學好課堂的作業設計與評價研究”研究成果】
參考文獻:
[1]謝廣珍.“雙減”政策下初中數學作業有效性的提升路徑[J].試題與研究,2023(02):46-48.
[2]郭驍安.“雙減”政策背景下豐富初中數學作業形式的策略探析[J].理科愛好者,2022(06):36-38.
[3]鄭珊.“雙減”視角下初中數學個性化作業設計對策分析[J].理科愛好者,2022(06):118-120.
[4]顧麗.提高初中數學“智慧作業”質量的有效策略[J].數理天地(初中版),2022(24):42-44.
[5]張淼.新課標下初中數學作業的優化設計思考[J].數學大世界(中旬),2021(03):79.

