通過“比的本質(zhì)再認識”達到概念深化

殷華 孫瑞 張維國 鞏子坤

摘 要：繼提出“同類量的比”與“不同類量的比”學(xué)習(xí)路徑之后，積極探尋新的路徑，帶領(lǐng)學(xué)生逐步脫離具體物體“量”的屬性，抽象出“數(shù)”的屬性，實現(xiàn)從“量”到“數(shù)”的跨越，從而深化對比概念的理解。具體而言，溝通比與除法、分數(shù)之間的關(guān)系，凸顯比的本質(zhì)；依托實例體會引入比的必要性，感受比的價值；經(jīng)歷從“量”的比到“數(shù)”的比的抽象過程，深化比的本質(zhì)。

關(guān)鍵詞：小學(xué)數(shù)學(xué)；比的認識；比的本質(zhì)；概念深化

本文系浙江省哲學(xué)社會科學(xué)規(guī)劃課題“基于認知發(fā)展模型的義務(wù)教育教科書編寫質(zhì)量提升研究”（編號：23NDJC265YB）、浙江省高校重大人文社科攻關(guān)計劃資助項目“建設(shè)高質(zhì)量教育體系背景下義務(wù)教育教科書編寫質(zhì)量提升路徑研究”（編號：2023GH005）的階段性研究成果。鞏子坤為本文通訊作者。

在“同類量的比”的學(xué)習(xí)中，學(xué)生理解“比表示兩個數(shù)量之間的一種倍數(shù)關(guān)系，比可以用分數(shù)的形式表示，兩個數(shù)的比也可以寫成兩個數(shù)相除的形式”，初步感知比與除法、分數(shù)的聯(lián)系。在“不同類量的比”的學(xué)習(xí)中，學(xué)生通過經(jīng)歷半直觀、半抽象的過程，進一步理解比的內(nèi)涵，了解不同類量的比，要去掉“名”，關(guān)注“數(shù)”，開始勾連貫通比與除法、分數(shù)。通過兩堂課的學(xué)習(xí)，學(xué)生已初步建立三者之間的聯(lián)系。

正如張奠宙教授所說，“返璞歸真，正本清源，是數(shù)學(xué)教學(xué)的一項基本原理”［1］。比的本質(zhì)如何學(xué)？不僅要幫助學(xué)生實現(xiàn)從“量”的比轉(zhuǎn)化為“數(shù)”的比，更應(yīng)當在引導(dǎo)學(xué)生溝通比與除法、分數(shù)三者關(guān)系的基礎(chǔ)上，給予學(xué)生更多的時間去感悟、體會“比”概念的意義和價值。盡管學(xué)生通過前兩堂課的學(xué)習(xí)，已有所感悟，但對“比”本質(zhì)的深層次理解仍不深刻。例如，當被問及“什么是比？”“學(xué)習(xí)了除法和分數(shù)之后，為什么還要學(xué)習(xí)比？”“同類量的比與不同類量的比之間有什么聯(lián)系與區(qū)別？”等問題時，學(xué)生還是無言以對。

對六年級學(xué)生來說，全面深入地理解和掌握比的概念絕非易事。這不僅依賴于教師的循序善誘，也受教材編排的影響。分析我國多版小學(xué)數(shù)學(xué)教材，發(fā)現(xiàn)它們在“溝通比與除法、分數(shù)三者關(guān)系”“深挖比的內(nèi)涵”上著墨不多，這在一定程度上給教學(xué)帶來了挑戰(zhàn)。

如何幫助學(xué)生建立比與除法、分數(shù)三者之間的聯(lián)系，達成對比的本質(zhì)再認識，是一線教師不斷探索和思考的方向。為此，我們在“同類量的比”與“不同類量的比”學(xué)習(xí)路徑之后，積極探尋新的路徑，以期在培養(yǎng)學(xué)生對比的本質(zhì)再認識的同時，也為今后一線教師關(guān)于“比的概念”教學(xué)提供參考。

一、研究設(shè)計

研究對象是深圳市一所普通小學(xué)六年級甲、乙兩個平行班（與開展“同類量的比”和“不同類量的比”教學(xué)實驗的班級相同）。由教師Y繼續(xù)授課。研究方法與流程同“同類量的比”和“不同類量的比”教學(xué)實驗，本文不再贅述。

（一） 問卷編制

為檢驗學(xué)生在經(jīng)過三堂課（《同類量的比》《不同類量的比》《比的本質(zhì)再認識》）的學(xué)習(xí)之后，是否達成了三個進階水平，設(shè)計后測問卷。具體內(nèi)容如下：

水平一：概念定義。具體含義：理解同類量比和不同類量比的意義，感受學(xué)習(xí)比的必要性。指標描述：理解比的意義；初步感受學(xué)習(xí)比的必要性；能解決比的實際問題。問卷題目：跑48 km大約需要6小時，路程與時間的比是（? ），比值是（? ），這個比值表示（? ）。

水平二：概念延展。具體含義：厘清比、分數(shù)、除法三者之間的關(guān)系，凸顯學(xué)習(xí)比的必要性。指標描述：結(jié)合生活實際，能建立比與除法、分數(shù)之間的聯(lián)系與區(qū)別，感受三者的內(nèi)在關(guān)系。問卷題目：跑48 km大約需要6小時，請用比、除法和分數(shù)表示路程與時間的關(guān)系，簡單說說三者的聯(lián)系與區(qū)別。

水平三：概念深化。具體含義：實現(xiàn)從“量”到“數(shù)”的跨越，引出兩個無量綱的數(shù)的比。指標描述：能探索解決探究性、開放性的關(guān)于比的非常規(guī)問題，體現(xiàn)比的獨特性。問卷題目：試著說一個能用“48∶6”表示的生活情境。

（二）計分標準

該問卷總分9分，各水平題目評分標準如下：

水平一：每空計1分，回答錯誤或者沒有回答計0分；

水平二：描述完整清晰計3分，簡單描述計2分，只寫關(guān)系式計1分，回答錯誤或者沒有回答計0分；

水平三：描述清晰完整計3分，簡單描述計2分，描述不完整計1分，回答錯誤或者沒有回答計0分。

二、研究過程與分析

（一）課前思考

在初構(gòu)學(xué)習(xí)路徑前，基于相關(guān)文獻、教材與學(xué)情分析，形成幾點思考：

1.精選問題情境，構(gòu)建比與除法、分數(shù)之間的關(guān)系

前兩條學(xué)習(xí)路徑（同類量的比、不同類量的比）均以“運動會”情境為依托展開教學(xué)，本條學(xué)習(xí)路徑是否也可以一以貫之，在“運動會”這個大背景下創(chuàng)設(shè)適當?shù)膯栴}情境，將比與除法、分數(shù)建立關(guān)系，從而更好地引領(lǐng)學(xué)生感悟比的本質(zhì)？北師大版小學(xué)數(shù)學(xué)六年級上冊配套的《教師用書》中指出，比的意義由除法發(fā)展而來，與除法、分數(shù)既有聯(lián)系又有區(qū)別；“比”強調(diào)的是量與量之間的倍比關(guān)系的直接描述，而除法、分數(shù)更多的是強調(diào)兩個量之間的一種運算關(guān)系，也會關(guān)注運算的結(jié)果。因此，選取怎樣的問題情境，幫助學(xué)生自然而然地將比與除法、分數(shù)建立關(guān)系，是促使學(xué)生感受三者聯(lián)系與區(qū)別的關(guān)鍵。

2.優(yōu)選生活實例，感受比的不可替代性

前兩條學(xué)習(xí)路徑都選取了一些生活實例幫助學(xué)生感受學(xué)習(xí)比的必要性，但學(xué)生還是存在“有些問題完全能用除法解決，為什么還要學(xué)習(xí)比”的困擾。比的哪些應(yīng)用是除法和分數(shù)無法取代的？生活中又有哪些典型素材能讓學(xué)生充分體會學(xué)習(xí)比的必要性？本條學(xué)習(xí)路徑應(yīng)選取更具典型性的生活實例，進一步幫助學(xué)生感受比的不可替代性。

3.巧選學(xué)習(xí)方式，深度理解比的本質(zhì)

張奠宙教授認為，比的概念有一個發(fā)展過程：最先是同類量的簡單倍數(shù)比較，然后是同類量的復(fù)雜比，再次是不同類量的比較，最后則是從“量”到“數(shù)”引出兩個無量綱的數(shù)的比［2］。因此，從“量”到“數(shù)”的比是一個多層抽象和高度概括的過程，需要經(jīng)歷從“狹義”到“廣義”的發(fā)展過程。選擇適當?shù)膶W(xué)習(xí)方式，讓學(xué)生深入淺出地體驗比的抽象過程，對學(xué)生深刻理解比的本質(zhì)尤為重要。

（二）學(xué)習(xí)路徑C1

1.任務(wù)介紹

任務(wù)1的目標：鞏固復(fù)習(xí)，簡述比的含義。具體內(nèi)容是：回顧所學(xué)，用自己的語言簡單描述對比的認識。教師通過詢問學(xué)生：前兩堂課我們都在學(xué)習(xí)比的知識，你能用自己的語言簡單描述一下什么是比嗎？以此勾起學(xué)生對比的回憶，起到鞏固復(fù)習(xí)的效果。

任務(wù)2的目標：創(chuàng)設(shè)情境，溝通比與除法、分數(shù)的關(guān)系。

子任務(wù)1：結(jié)合情境提出問題，選擇比、除法或分數(shù)的形式列式解答。教師延續(xù)前兩堂課的運動會情境：“小輝分別參加了50米和200米跑步比賽，觀察表1，用你喜歡的方式描述小輝在哪項運動中發(fā)揮得更好？”

學(xué)生大致給出三種做法：

①50÷8=6.25（米/秒），200÷40=5（米/秒）。

②50∶8=50÷8，200∶4=200÷40。

③50∶8=50÷8=508，200∶4=200÷40=2004。

觀察做法③中的兩個等式，它們體現(xiàn)了比與除法、分數(shù)之間的關(guān)系，這也成為教師帶領(lǐng)學(xué)生溝通三者關(guān)系的突破口。

子任務(wù)2：觀察等式和表格，分析討論三者的聯(lián)系與區(qū)別。基于學(xué)生在前兩堂課中的表現(xiàn)，認為學(xué)生在比與除法、分數(shù)三者關(guān)系的描述上存在一定難度。于是，教師在本堂課的學(xué)習(xí)單中增添了“比”一欄內(nèi)容（見表2）。利用等式和表格，幫助學(xué)生有方向地填寫“除法”與“分數(shù)”中的內(nèi)容，分析得到三者之間的聯(lián)系與區(qū)別，從而凸顯比的內(nèi)涵。

以下是課堂實錄片段：

師 觀察黑板上的關(guān)系式50∶8=50÷8=508，小組討論，每個表達式中各部分的名稱是什么？

生 “50∶8”中，“50”是比的前項，“：”是比號，“8”是比的后項，“508”是比值。

生 “50÷8”中，“50”表示被除數(shù)，“8”表示除數(shù)，“508”是商。

生 “508”中，“50”是分子，“8”是分母，“508”是一個分數(shù)。

師 既然三個表達式能用“=”號相連，它們之間肯定存在一定的關(guān)系。現(xiàn)在請大家拿出課堂學(xué)習(xí)單，四人小組再次合作，可以橫著看，也可以豎著看，找一找比與除法、分數(shù)之間的聯(lián)系與區(qū)別。

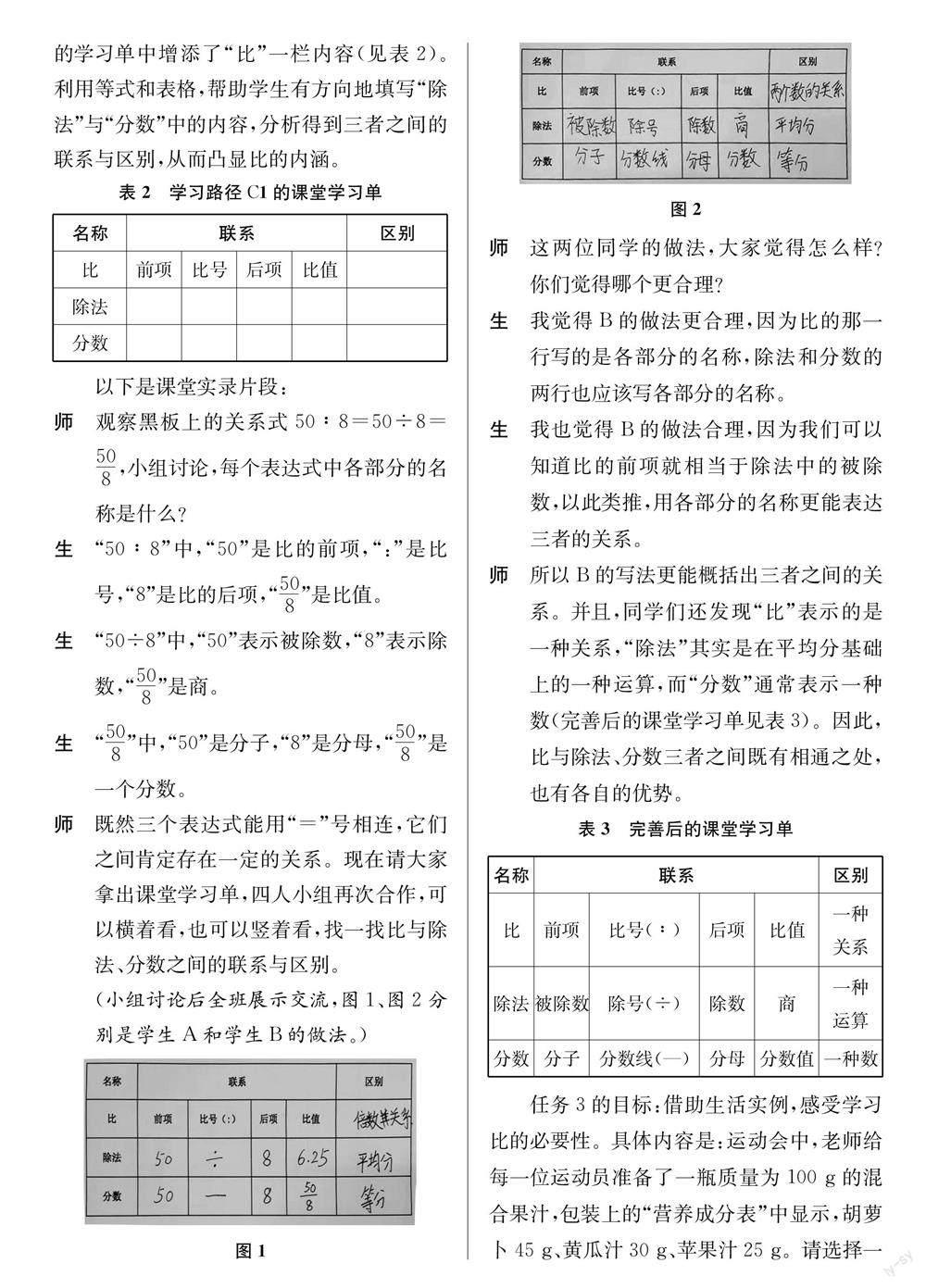
（小組討論后全班展示交流，圖1、圖2分別是學(xué)生A和學(xué)生B的做法。）

師 這兩位同學(xué)的做法，大家覺得怎么樣？你們覺得哪個更合理？

生 我覺得B的做法更合理，因為比的那一行寫的是各部分的名稱，除法和分數(shù)的兩行也應(yīng)該寫各部分的名稱。

生 我也覺得B的做法合理，因為我們可以知道比的前項就相當于除法中的被除數(shù)，以此類推，用各部分的名稱更能表達三者的關(guān)系。

師 所以B的寫法更能概括出三者之間的關(guān)系。并且，同學(xué)們還發(fā)現(xiàn)“比”表示的是一種關(guān)系，“除法”其實是在平均分基礎(chǔ)上的一種運算，而“分數(shù)”通常表示一種數(shù)（完善后的課堂學(xué)習(xí)單見表3）。因此，比與除法、分數(shù)三者之間既有相通之處，也有各自的優(yōu)勢。

任務(wù)3的目標：借助生活實例，感受學(xué)習(xí)比的必要性。具體內(nèi)容是：運動會中，老師給每一位運動員準備了一瓶質(zhì)量為100 g的混合果汁，包裝上的“營養(yǎng)成分表”中顯示，胡蘿卜45 g、黃瓜汁30 g、蘋果汁25 g。請選擇一種合適的方式表示出營養(yǎng)表中三種成分之間的關(guān)系。學(xué)生寫出45∶30∶25。教師引導(dǎo)思考：為什么用比的形式表示更合適？討論并小結(jié)：比的形式既能表示量與量之間的關(guān)系，又能具體看出每一個量的多少;而除法、分數(shù)更多的是強調(diào)量與量之間的一種運算關(guān)系或運算的結(jié)果。教師通過這一生活實例，引導(dǎo)學(xué)生進一步體會學(xué)習(xí)比的必要性。

任務(wù)4的目標：梳理知識框架，深度理解比的本質(zhì)。具體內(nèi)容是：梳理三堂課的知識點，通過不同類型樣例的勾連，實現(xiàn)比的抽象。為引導(dǎo)學(xué)生對三堂課的知識點進行梳理，從而勾連“同類量的比”與“不同類量的比”，實現(xiàn)比從“量”到“數(shù)”的抽象，教師借助情境不同但數(shù)字相同的比，請學(xué)生分別回答問題：（1）我有4支鉛筆，你有3支鉛筆，求兩個人鉛筆支數(shù)的比？（2）4顆智慧星換3支鉛筆，求智慧星數(shù)量與鉛筆支數(shù)的比？在解答過程中，學(xué)生會發(fā)現(xiàn)不論是同類量之比（4支∶3支）還是非同類量之比（4顆∶3支），去掉單位后都可以抽象為數(shù)的比（4∶3），從而感受到雖然在結(jié)果中前者無量綱，后者有量綱，但最終都是將“量”的比抽象為“數(shù)”的比。

2.問題分析

（1）任務(wù)1中產(chǎn)生的復(fù)習(xí)效果不明顯

雖然教師勾起了學(xué)生對比的回憶，但有些學(xué)生只能淺層次地描述一兩句，或簡單地舉一個用比解決的問題。這都沒有涉及同類量比和不同類量比的聯(lián)系，使得整體復(fù)習(xí)效果仍不夠顯著。

（2）任務(wù)2中的情境容易限制學(xué)生的思維

大部分學(xué)生會利用數(shù)量關(guān)系式“路程÷時間=速度”來解決問題，而寫比和分數(shù)形式的人數(shù)并不多，其原因可能在于該情境限制了學(xué)生的思維。并且，該任務(wù)要求學(xué)生厘清三者的區(qū)別，這對學(xué)生而言存在一定的難度，不利于后續(xù)教學(xué)的開展。

（3）任務(wù)3中選取的實例不夠典型，無法體現(xiàn)學(xué)習(xí)比的必要性

此任務(wù)的設(shè)計意圖是讓學(xué)生感悟比既能表示多個量之間的關(guān)系，又能具體顯示每一個量的多少。但在實際操作時，由于學(xué)生認知中對除法的深刻印象和廣泛應(yīng)用，使得他們首先會想到用除法分別表示兩個量之間的關(guān)系，如用45÷30、30÷25、45÷25分別描述三個量之間的關(guān)系。此外，三個量之間的比對學(xué)生來說是較特殊的情況，不利于學(xué)生從中體會比的必要性。

（4）任務(wù)4中引發(fā)的學(xué)習(xí)方式不夠開放

教師一直在試圖牽引學(xué)生搭建比的知識框架。在從“量”到“數(shù)”的比這一抽象過程中，教師參與過多，學(xué)生只能被動接受所學(xué)知識，并沒有很好地體現(xiàn)“以學(xué)生為中心”的理念，也不利于學(xué)生對比本質(zhì)的理解。

3.修改建議

（1）創(chuàng)設(shè)情境，進一步建立比與除法、分數(shù)的聯(lián)系

刪除任務(wù)1中的復(fù)習(xí)活動，開門見山地引出情境。

對任務(wù)2，改變之前“小輝分別參加了50米和200米跑步比賽”的情境，創(chuàng)設(shè)“學(xué)校秋季運動會中，老師給小輝班的每一位運動員準備了一瓶混合果汁，每瓶果汁里有蘋果汁20 g、橙汁40 g。請用除法或者比的形式表示兩種果汁之間的關(guān)系”這一情境。這里只提到了“用除法或者比的形式表示兩種果汁之間的關(guān)系”，并沒有提到用分數(shù)的形式表示。原因在于寫除法算式時，學(xué)生有得商的習(xí)慣，必定會將分數(shù)與除法建立聯(lián)系，這就可以將三者之間的關(guān)系溝通起來。同時，對分數(shù)是一種數(shù)的感受更明顯。

在觀察a∶b=a÷b=ab（b≠0）形式的等式后，利用表格對三者的關(guān)系進行整體的對比分析，有助于學(xué)生深挖比的內(nèi)涵。同時，建議在任務(wù)2中先建立三者之間的聯(lián)系，等任務(wù)3完成之后再補充三者之間的區(qū)別。

（2）借助實例，感受學(xué)習(xí)比的必要性

教師應(yīng)多舉一些類似于“飲料配比”的生活實例，讓學(xué)生充分感受比在生活中的存在價值。如和面時水與面的比、洗衣服時水與洗衣液的比，等等。

（3）提出問題，實現(xiàn)比的抽象過程

教師任意給出兩個數(shù)的比，如5∶4，引導(dǎo)學(xué)生結(jié)合生活體驗，試著說一個用“5∶4”表示的情境。學(xué)生會賦予“5∶4”很多不同的情境，其中會出現(xiàn)同類量的比，也會有不同類量的比。在舉了大量的情境之后，再引導(dǎo)學(xué)生逆轉(zhuǎn)思維拋開情境，感受脫離具體的“量”抽象出“數(shù)”的屬性的過程。這樣的設(shè)計，使得課堂更加開放，也有助于學(xué)生在自由探索中深化對比本質(zhì)的理解。

（三）學(xué)習(xí)路徑C2

學(xué)習(xí)路徑C2的最大特點是巧用材料，驅(qū)動學(xué)生深入學(xué)習(xí)。每個環(huán)節(jié)都給學(xué)生提供不同形式的“腳手架”，借助情境、等式、實例、問題等載體，讓學(xué)生有理可依、有話可說，幫助學(xué)生逐層體會比的本質(zhì)。

1.任務(wù)介紹

任務(wù)1的目標：創(chuàng)設(shè)情境，溝通比與除法、分數(shù)之間的關(guān)系。具體內(nèi)容是：創(chuàng)設(shè)情境，用除法或比表示果汁中兩種成分的關(guān)系，并說明理由。

任務(wù)2的目標：借助等式，溝通比與除法、分數(shù)之間的關(guān)系。具體內(nèi)容是：借助等式和表格，梳理三者之間的聯(lián)系。

任務(wù)1和任務(wù)2依托問題情境“學(xué)校秋季運動會中，老師給小輝班的每一位運動員準備了一瓶混合果汁，每瓶果汁里有蘋果汁20 g、橙汁40 g。請用除法或者比的形式表示兩種果汁之間的關(guān)系”展開教學(xué)，學(xué)生可以將前兩堂課對比的認識重新加以梳理，借助等式20∶40=20÷40=12，建立比與除法、分數(shù)的關(guān)系，初步感受比的不同之處。

任務(wù)3的目標：巧取實例，體會學(xué)習(xí)比的必要性。子任務(wù)1：呈現(xiàn)生活中兩個或多個量之間比的實例，進一步體會學(xué)習(xí)比的必要性。子任務(wù)2：補充比與除法、分數(shù)的區(qū)別，感悟比的不可替代性。“比”這一概念的獨特性體現(xiàn)在哪里？

“兩個數(shù)相除又叫作兩個數(shù)的比”這一說法不能全面揭示引入“比”概念的獨特價值，即區(qū)別于“除法”的本質(zhì)特征。也許正是源于這一問題的困擾，學(xué)生不愿意承認“兩個數(shù)相除又叫作兩個數(shù)的比”。因此，子任務(wù)1中，教師為學(xué)生提供了大量“比”的素材，這些素材都在不斷強調(diào)比的意義，以此突出“除法”之外的特定內(nèi)涵。學(xué)生通過接觸如此豐富的貼近自己生活的實例，感受到比不同于除法之處，感受到它的不可代替性，即比能更清晰地表示兩個數(shù)量之間的倍數(shù)關(guān)系。如：做雞蛋羹時雞蛋和水的比是1∶1；做面包時，高筋面粉與牛奶的比是1∶5；做饅頭時，水、面粉和酵母粉的比是100∶50∶1；洗衣服時，洗衣液與水的比是1∶20到1∶30；家庭收入與花銷的比是3∶1。而在子任務(wù)2中，教師將之前任務(wù)中沒有完成的“比與除法、分數(shù)之間的區(qū)別”放在此處解決，好處有兩點：一是子任務(wù)1中大量的實例讓學(xué)生對比的意義有了進一步的體會，他們對“比表示一種關(guān)系”的理解更加深刻；二是通過子任務(wù)1的學(xué)習(xí)，學(xué)生感受到“除法也有表示兩者關(guān)系的含義，但更多的是一種運算”，而“分數(shù)通常表示一種數(shù)”。

任務(wù)4的目標：依托問題，感受從量的比抽象為數(shù)的比的過程，理解比的本質(zhì)。子任務(wù)1：試著說一個能用“4∶3”表示的生活情境。子任務(wù)2：拋開情境，感受從“量”到“數(shù)”的比的抽象過程。“比”的概念是在抽象的數(shù)學(xué)理論和眾多實例基礎(chǔ)上通過層級抽象所得到的。各個版本教材盡管在處理方式上有所不同，但都是通過設(shè)計豐富的情境，如國旗的長與寬的關(guān)系、路程與時間的關(guān)系等，在引導(dǎo)學(xué)生充分感知和體會的基礎(chǔ)上，幫助學(xué)生抽象出比的本質(zhì)是“數(shù)量之間的倍數(shù)關(guān)系”。該任務(wù)試圖在此基礎(chǔ)上對比的本質(zhì)做進一步抽象與提升，讓學(xué)生意識到“數(shù)量之間的比本質(zhì)上就是數(shù)之間的比”。這一環(huán)節(jié)利用“試著說一個能用‘4∶3表示的生活情境”這一問題，讓學(xué)生發(fā)揮自己的想象力靈活舉例。學(xué)生有的提出“同類量的比”的例子，有的提出“不同類量的比”的例子。學(xué)生暢所欲言后會發(fā)現(xiàn)，拋開情境，其實都是在描述4與3這兩個數(shù)之間的倍數(shù)關(guān)系，幫助學(xué)生理解“量”之間的比本質(zhì)上就是“數(shù)”之間的比。

以下是課堂實錄片段：

師 你能試著說一個用“20∶40”表示的情境嗎？

生 長方形的寬和長的比是20∶40。它們是兩個長度之間的比，是同類量的比。

生 路程與時間的比是20∶40。它們是不同類量的比，兩個不同類量的比產(chǎn)生了一個新的量——速度。

生 20個正方形與40個正方形的比是20∶40。

師 同樣是20∶40，既可以描述同類量的倍數(shù)關(guān)系，也可以描述非同類量的倍數(shù)關(guān)系，只不過情境不同。拋開情境，其實都是在描述20與40這兩個數(shù)之間的倍數(shù)關(guān)系。所以，“量”之間的比本質(zhì)上就是“數(shù)”之間的比。

2.教學(xué)效果

通過對甲、乙班的后測結(jié)果進行統(tǒng)計，得到后測中各個題目的平均正確率（見表4）。

從統(tǒng)計結(jié)果來看，乙班學(xué)生在各個題目上的正確率均優(yōu)于甲班。分別對兩班學(xué)生的3道小題得分進行獨立樣本t檢驗，結(jié)果表明，兩班學(xué)生在第1題上不存在顯著性差異（t=－5.620，p=0.372），在第2題上存在顯著性差異（t=－2.147，p<0.05），在第3題上存在顯著性差異（t=－3.477，p<0.01）。

盡管在第1題上兩班學(xué)生不存在顯著性差異，但結(jié)合學(xué)生的課堂表現(xiàn)以及教師的執(zhí)教感受，仍能認為乙班學(xué)生對比的意義理解更加深刻。可見，經(jīng)過兩輪教學(xué)實施對比發(fā)現(xiàn)，采用優(yōu)化的學(xué)習(xí)路徑C2相對于學(xué)習(xí)路徑C1的效果更好。學(xué)生不僅能更完整清晰地描述比相對于除法、分數(shù)的不可替代性，還能深刻理解比的價值和內(nèi)涵，為后續(xù)正比例的學(xué)習(xí)做好充分準備。

三、研究結(jié)論與建議

（一）結(jié)論

“比的本質(zhì)再認識”的學(xué)習(xí)，在于幫助學(xué)生實現(xiàn)從“量”的比到“數(shù)”的比的抽象，并在溝通比與除法、分數(shù)關(guān)系的基礎(chǔ)上，體會“比”這一概念的意義和價值。為此，研究通過三次研討、兩次教學(xué)，最終得到完善的學(xué)習(xí)路徑，主要分為三步走：（1）溝通聯(lián)系，通過創(chuàng)設(shè)情境，用除法或比的形式表示果汁中兩種成分的關(guān)系，將比與除法、分數(shù)三者進行勾連，借助等式與表格，梳理三者之間的聯(lián)系，凸顯比的本質(zhì)；（2）感受價值，借助貼近學(xué)生生活的大量實例，如洗衣時洗衣液與水的比、家庭收入與花銷的比等，體會比的獨特性與不可替代性，感受比的價值；（3）深化本質(zhì)，依托問題“試著說一個用‘20∶40表示的情境”，引導(dǎo)學(xué)生意識到“量之間的比本質(zhì)上就是數(shù)之間的比”，經(jīng)歷從量的比抽象為數(shù)的比的過程，深化比的本質(zhì)。

同時，后測表明，乙班學(xué)生在三個水平上的得分均高于甲班學(xué)生，尤其是“概念深化”水平。由此表明：優(yōu)化后的學(xué)習(xí)路徑，有助于加深學(xué)生對比概念本質(zhì)的理解，深刻建立起比與除法、分數(shù)之間的聯(lián)系。但就部分學(xué)生的表現(xiàn)仍能看出，他們對三者之間聯(lián)系的理解存在困難。至于這個知識點該怎樣處理更利于學(xué)生深化理解比的本質(zhì)，期待進一步的研究來檢驗。

（二）建議

教材修訂時，為了引導(dǎo)學(xué)生進一步認識相關(guān)概念之間的聯(lián)系與區(qū)別，可以增加一個小問題：“想一想，比與除法、分數(shù)有什么關(guān)系？與同伴交流。”其目的在于促使學(xué)生建立三者之間的關(guān)系。這個問題看似簡單，但要厘清比與除法、分數(shù)之間的聯(lián)系與區(qū)別，對學(xué)生來說也是一個難點。因此，教材可以補充合適的情境，提出“比的前項、后項和比值分別相當于除法算式和分數(shù)中的什么？比的后項可以是0嗎？”等具體問題，以此幫助學(xué)生更好地開展學(xué)習(xí)。

教師教學(xué)時，要厘清比概念的發(fā)生發(fā)展過程，搭建比概念的整體架構(gòu)（從理解比的概念到延展比的內(nèi)涵，再到深化比的本質(zhì)）。此外，比的概念教學(xué)，需要從比的產(chǎn)生、比的應(yīng)用、比例等更高的層次出發(fā)，設(shè)計一系列有梯度的教學(xué)活動，為學(xué)生的長遠發(fā)展著想。

學(xué)生學(xué)習(xí)時，要注重知識的主動建構(gòu)過程。對“比”的概念建立起從感性到理性的認識，要有足夠的時間和空間去觀察、思辨和探究，從而建構(gòu)對比的概念的整體認知。

參考文獻：

［1］［2］ 張奠宙.返璞歸真 正本清源——“比”不能等同于除法［J］.教學(xué)月刊·小學(xué)版（數(shù)學(xué)），2015（3）：4－8+1.