可降階的高階微分方程中的一個(gè)教學(xué)案例

劉海濤 鐘文敏 李響軍

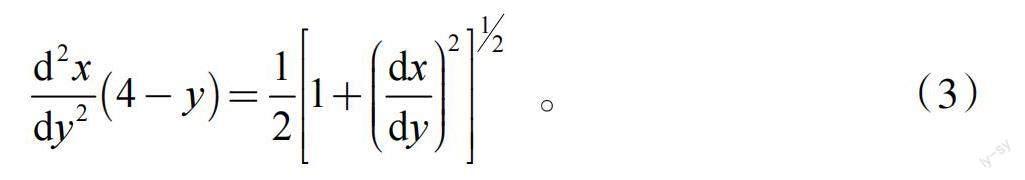
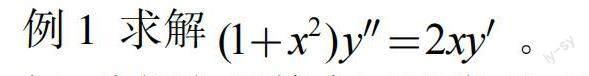
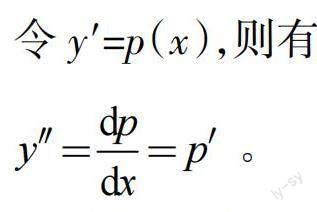
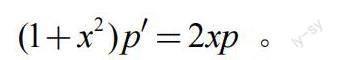
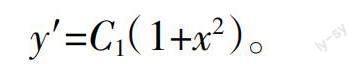
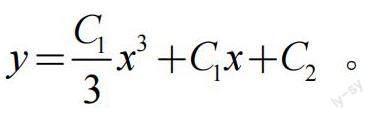
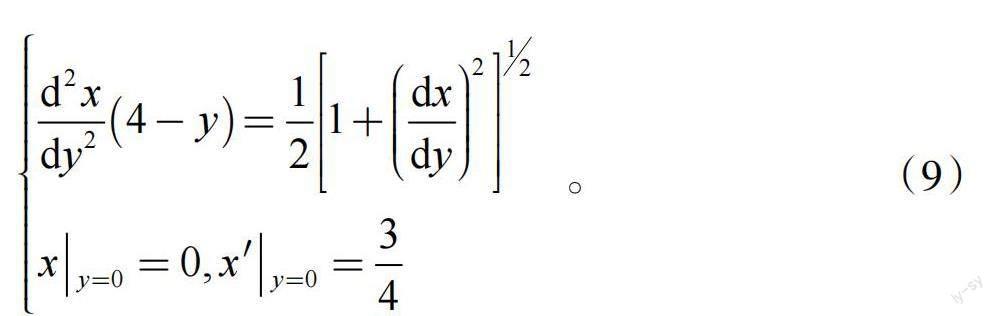
摘? 要：針對(duì)本科高等數(shù)學(xué)課程中可降階微分方程教學(xué)內(nèi)容的特點(diǎn)以及軍隊(duì)院校育人要求，為了更好地提高學(xué)生學(xué)習(xí)積極性、培養(yǎng)學(xué)生數(shù)學(xué)應(yīng)用能力，以導(dǎo)彈飛行軌跡問(wèn)題為切入點(diǎn)設(shè)計(jì)教學(xué)案例，通過(guò)創(chuàng)設(shè)情景、提出問(wèn)題，引導(dǎo)討論、建立模型，歸納分析、引出教學(xué)內(nèi)容，分析討論、講解求解方法，回歸問(wèn)題、培養(yǎng)應(yīng)用能力等五個(gè)環(huán)節(jié)，對(duì)教學(xué)過(guò)程進(jìn)行重新設(shè)計(jì)，方便教師使用。

關(guān)鍵詞：教學(xué)案例；可降階的高階微分方程；高等數(shù)學(xué)；數(shù)學(xué)應(yīng)用能力；教學(xué)設(shè)計(jì)

中圖分類(lèi)號(hào)：G642? ? ? 文獻(xiàn)標(biāo)志碼：A? ? ? ? ?文章編號(hào)：2096-000X（2023）32-0099-04

Abstract： In view of the characteristics of reducible higher order differential equations in Higher Mathematics of the undergraduate course， and the education requirement of military academies， in order to improve students' enthusiasm for learning and cultivate their mathematical application ability， the teaching case is designed with the missile flight trajectory as the starting point. Through creating scenarios and raising questions， guiding discussion and giving cases， summing up and leading to the teaching content， analyzing， discussing and explaining the method， returning to the problem and cultivating application ability， the teaching process has been redesigned for the convenience of teachers.

Keywords： teaching case; reducible higher order differential equations; Higher Mathematics; mathematics application ability; teaching design

基金項(xiàng)目：軍隊(duì)院校教學(xué)成果立項(xiàng)培育項(xiàng)目“為戰(zhàn)育人導(dǎo)向下的《工程數(shù)學(xué)》課程教學(xué)改革實(shí)踐”（NUE2022TA01）

第一作者簡(jiǎn)介：劉海濤（1982-），男，漢族，河北廊坊人，博士，副教授。研究方向?yàn)閼?yīng)用數(shù)學(xué)。

微分方程是高等數(shù)學(xué)中一個(gè)重要教學(xué)內(nèi)容，在同濟(jì)大學(xué)第七版《高等數(shù)學(xué)》教材中出現(xiàn)在第七章，對(duì)于培養(yǎng)學(xué)生抽象思維和分析解決實(shí)際問(wèn)題的能力有重要作用[1]。通常，大學(xué)一年級(jí)學(xué)生往往求知欲旺盛，在學(xué)習(xí)過(guò)程中希望學(xué)以致用。特別是對(duì)軍隊(duì)院校大學(xué)一年級(jí)學(xué)員而言，濃厚的軍營(yíng)氛圍以及未來(lái)的崗位特點(diǎn)使他們更希望將所學(xué)知識(shí)與軍事問(wèn)題聯(lián)系起來(lái)。為了調(diào)動(dòng)學(xué)員的學(xué)習(xí)積極性，培養(yǎng)學(xué)員數(shù)學(xué)應(yīng)用能力，本文設(shè)計(jì)了一個(gè)有軍事背景的以導(dǎo)彈飛行軌跡問(wèn)題為切入點(diǎn)的教學(xué)案例，旨在激發(fā)學(xué)生的學(xué)習(xí)興趣，引導(dǎo)其將理論與實(shí)踐聯(lián)系起來(lái)，提高創(chuàng)新意識(shí)和創(chuàng)造能力[2-3]。

在此部分教學(xué)內(nèi)容之前，學(xué)生已經(jīng)學(xué)習(xí)了一元微積分學(xué)，以及幾種典型的一階微分方程及其解法，從而對(duì)于微分方程形成了一些基本的認(rèn)識(shí)。而本節(jié)內(nèi)容即可降階的高階微分方程則是微分方程教學(xué)內(nèi)容的又一個(gè)重要組成部分，主要體現(xiàn)在：首先，本節(jié)教學(xué)內(nèi)容是學(xué)生第一次接觸高階微分方程，是他們學(xué)習(xí)更多不同類(lèi)型微分方程的過(guò)渡和橋梁；其次，本次教學(xué)內(nèi)容中的“降階法”，是求解許多高階微分方程的一種基本思路，對(duì)于后續(xù)課程的學(xué)習(xí)乃至一些實(shí)際問(wèn)題的解決都有重要作用。

傳統(tǒng)教學(xué)方法通常是以分析可降階微分方程的特點(diǎn)為思路引出這部分教學(xué)內(nèi)容，這對(duì)于學(xué)生掌握好這部分理論知識(shí)固然重要，但純粹從數(shù)學(xué)知識(shí)體系角度設(shè)計(jì)的教學(xué)過(guò)程難免顯得枯燥，不容易引起學(xué)生的學(xué)習(xí)興趣。探究式教學(xué)和案例式教學(xué)以具體問(wèn)題為引入，對(duì)于調(diào)動(dòng)學(xué)生的學(xué)習(xí)積極性有很好的作用，同時(shí)通過(guò)創(chuàng)設(shè)有軍事背景的問(wèn)題情境，并以問(wèn)題為牽引的方式開(kāi)展教學(xué)，有助于更好地調(diào)動(dòng)學(xué)生的學(xué)習(xí)狀態(tài)，培養(yǎng)學(xué)生的分析問(wèn)題、解決問(wèn)題的能力[4-5]。基于此，本文通過(guò)抽象和簡(jiǎn)化，給出一個(gè)基于導(dǎo)彈飛行軌跡問(wèn)題的教學(xué)案例，方便教師在教學(xué)過(guò)程中使用。

一? 教學(xué)目標(biāo)

通過(guò)本次課的課堂教學(xué)，使學(xué)生達(dá)到以下目標(biāo)：一是會(huì)辨識(shí)常見(jiàn)的可以用降階法求解的微分方程；二是掌握可降階微分方程的求解方法，領(lǐng)會(huì)“降階法”的基本思想；三是通過(guò)利用所學(xué)知識(shí)解決導(dǎo)彈飛行軌跡問(wèn)題，提高分析問(wèn)題、解決問(wèn)題的能力。

二? 教學(xué)設(shè)計(jì)

本案例主要討論一種可以用降階法求解的高階微分方程。首先通過(guò)一個(gè)學(xué)員較感興趣的軍事問(wèn)題引入；然后，分析該問(wèn)題的特點(diǎn)，并引出教學(xué)內(nèi)容；接著，研究討論解決該問(wèn)題的方法；最后解決開(kāi)頭提出的軍事問(wèn)題。

根據(jù)上述分析，將教學(xué)流程設(shè)計(jì)為以下五個(gè)環(huán)節(jié)。

第一，創(chuàng)設(shè)情境，提出問(wèn)題。通過(guò)一個(gè)學(xué)生較感興趣的軍事問(wèn)題，適當(dāng)配以視頻、文字等素材創(chuàng)設(shè)情境并提出問(wèn)題，即如何確定導(dǎo)彈在跟蹤和命中空中目標(biāo)過(guò)程中的飛行軌跡。

第二，引導(dǎo)討論，建立模型。對(duì)問(wèn)題進(jìn)行適當(dāng)抽象和簡(jiǎn)化，通過(guò)建立該問(wèn)題的數(shù)學(xué)模型，得到描述該問(wèn)題的微分方程。

第三，歸納分析，引出教學(xué)內(nèi)容。通過(guò)分析歸納該方程的特點(diǎn)，引出教學(xué)內(nèi)容，即可降階的高階微分方程。

第四，分析討論，講解求解方法。通過(guò)分析微分方程的特點(diǎn)，提煉出用降階法求解微分方程的一般過(guò)程，并結(jié)合例題加以鞏固。

第五，回歸問(wèn)題，培養(yǎng)應(yīng)用能力。利用所學(xué)方法解決開(kāi)頭提出的導(dǎo)彈飛行軌跡確定問(wèn)題，激發(fā)學(xué)習(xí)興趣，提高學(xué)生的數(shù)學(xué)應(yīng)用能力。

三? 教學(xué)流程

（一）? 創(chuàng)設(shè)情境，提出問(wèn)題

針對(duì)軍校學(xué)員的專(zhuān)業(yè)背景特點(diǎn)，建議選取已公開(kāi)的導(dǎo)彈射擊演練視頻作為課程的起始，以此創(chuàng)設(shè)教學(xué)情境，使學(xué)員迅速進(jìn)入良好的學(xué)習(xí)狀態(tài)。通常，導(dǎo)彈跟蹤和命中空中目標(biāo)的過(guò)程可以分為三個(gè)階段：一是偵察預(yù)警系統(tǒng)將目標(biāo)運(yùn)動(dòng)軌跡、飛行速度等實(shí)時(shí)參數(shù)通過(guò)信息系統(tǒng)同步發(fā)送到導(dǎo)彈發(fā)射平臺(tái)；二是導(dǎo)彈發(fā)射平臺(tái)自動(dòng)計(jì)算射擊諸元，完成射擊準(zhǔn)備；三是發(fā)射導(dǎo)彈，跟蹤并命中空中目標(biāo)。

由于整個(gè)過(guò)程是一個(gè)十分復(fù)雜的系統(tǒng)工程，因此，需要引導(dǎo)學(xué)員關(guān)注與本次課程內(nèi)容緊密相關(guān)的部分，即在第二階段導(dǎo)彈發(fā)射平臺(tái)在進(jìn)行射擊準(zhǔn)備的過(guò)程中，如何確定導(dǎo)彈的飛行軌跡？

至此，創(chuàng)設(shè)情境環(huán)節(jié)結(jié)束，整個(gè)過(guò)程持續(xù)約2～3分鐘，并由此轉(zhuǎn)入下一階段，即引導(dǎo)學(xué)員參與討論，進(jìn)而建立該問(wèn)題的數(shù)學(xué)模型。

（二）? 引導(dǎo)討論，建立模型

一般而言，由于實(shí)際問(wèn)題往往較為復(fù)雜，因此為了用數(shù)學(xué)方法加以解決，常常需要通過(guò)抽象和簡(jiǎn)化，建立其數(shù)學(xué)模型。從另一個(gè)角度看，正是由于高等數(shù)學(xué)教學(xué)內(nèi)容非常抽象，因此只有建立了實(shí)際問(wèn)題的數(shù)學(xué)模型，才能更好地將其與所學(xué)知識(shí)緊密關(guān)聯(lián)起來(lái)。

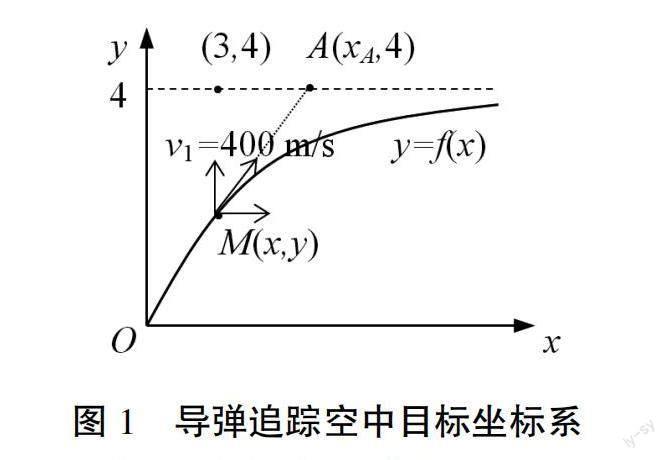
針對(duì)導(dǎo)彈飛行軌跡確定問(wèn)題，首先需要建立描述該問(wèn)題的直角坐標(biāo)系。假設(shè)在發(fā)射時(shí)刻t=0時(shí)，導(dǎo)彈位于坐標(biāo)原點(diǎn)，不妨假設(shè)空中目標(biāo)位于點(diǎn)（3，4），并且以200 m/s的速度沿x軸正向飛行。

接著，不妨假設(shè)導(dǎo)彈飛行速度為400 m/s，并且導(dǎo)彈采取的導(dǎo)引律為“尾追法”，即其在飛行過(guò)程中始終指向空中目標(biāo)。為了求出導(dǎo)彈的飛行軌跡，記其飛行軌跡為函數(shù)y=f（x）。顯然，飛行軌跡函數(shù)中的x，y都是時(shí)刻t的函數(shù)，因此要求出該函數(shù)，就需要分析x，y隨時(shí)間的t的變化規(guī)律。

記導(dǎo)彈在t時(shí)刻位于點(diǎn)M（x，y），根據(jù)已知條件，導(dǎo)彈在飛行過(guò)程中始終指向空中目標(biāo)，因此導(dǎo)彈的速度方向始終與導(dǎo)彈當(dāng)前位置M點(diǎn)與目標(biāo)t時(shí)刻位置A點(diǎn)的連線(xiàn)一致。

設(shè)空中目標(biāo)在t時(shí)刻的位置坐標(biāo)是（xA，4）。則由于目標(biāo)的初始位置是點(diǎn)（3，4），而飛行速度是200 m/s，因此容易得到A點(diǎn)的橫坐標(biāo)為xA=3+200 t。

又因?yàn)閷?dǎo)彈始終指向目標(biāo)，因此點(diǎn)M處的切線(xiàn)斜率等于M點(diǎn)和A點(diǎn)連線(xiàn)的斜率，即

再把導(dǎo)彈的速度進(jìn)行分解，兩個(gè)沿坐標(biāo)軸的分速度的平方和即為導(dǎo)彈速度的平方，由此得到

利用所得到的式（1）和式（2），通過(guò)整理消掉變量t，就可以得到導(dǎo)彈運(yùn)動(dòng)軌跡滿(mǎn)足的微分方程為

求解出這個(gè)微分方程，就可以確定導(dǎo)彈飛行軌跡。也就是說(shuō)導(dǎo)彈飛行軌跡的確定問(wèn)題轉(zhuǎn)化為了高階微分方程的求解問(wèn)題。

該過(guò)程大約持續(xù)4～5分鐘。由此轉(zhuǎn)入下一環(huán)節(jié)，即通過(guò)歸納和分析，引出本次課的教學(xué)內(nèi)容。

（三）? 歸納分析，引出教學(xué)內(nèi)容

由于本次課教學(xué)內(nèi)容是可降階的高階微分方程，因此需要通過(guò)歸納分析微分方程式（3）的一般特點(diǎn)，進(jìn)而引出教學(xué)內(nèi)容。

首先，復(fù)習(xí)微分方程的“階”的定義，并由此指出，該微分方程是一個(gè)高階微分方程。事實(shí)上，根據(jù)前面的學(xué)習(xí)可知，微分方程的“階”是指方程中未知函數(shù)的最高階導(dǎo)數(shù)的階數(shù)。具體到上述飛行軌跡方程，由于變量x是未知函數(shù)，而變量y是自變量，因此這個(gè)方程階是2。

再進(jìn)一步，在這個(gè)方程中除了未知函數(shù)的導(dǎo)數(shù)，只有自變量y而沒(méi)有未知函數(shù)x。因此可以將其特點(diǎn)歸納為：不顯含未知函數(shù)的二階微分方程。其一般形式是

需要注意的是，在此過(guò)程中應(yīng)提醒學(xué)生：盡管出于習(xí)慣，我們常常是把y看作未知函數(shù)，而把x看作自變量，但這不是必須的，例如在方程式（3）中就把變量x看作未知函數(shù)。

（四）? 分析討論，講解求解方法

經(jīng)過(guò)上述幾個(gè)環(huán)節(jié)，大約使用8分鐘時(shí)間完成了創(chuàng)設(shè)情境、建立模型和引出教學(xué)內(nèi)容等步驟，接下來(lái)進(jìn)入分析討論、知識(shí)講解環(huán)節(jié)。

首先從認(rèn)識(shí)論認(rèn)知心理學(xué)的角度看，當(dāng)我們面對(duì)一個(gè)新問(wèn)題時(shí)，往往首先考慮的借助與之相關(guān)的、已經(jīng)掌握的方法來(lái)解決它。因此，對(duì)于高階微分方程，一種自然也重要的思路是：將高階微分方程的階降低，轉(zhuǎn)化為一階微分方程，再來(lái)進(jìn)行求解。

因此，接下來(lái)引導(dǎo)學(xué)員觀(guān)察式（4）：由于方程中只出現(xiàn)了二階導(dǎo)數(shù)，因此若把y′看作一個(gè)整體，用一個(gè)新的未知函數(shù)來(lái)代替它（即變量代換），例如令y′=p，則方程的階就可以降低。

嘗試令y′=p（x），并且兩邊同時(shí)對(duì)x求導(dǎo)數(shù)，可得

將式（5）代入原方程得到

至此可得到一個(gè)以x為自變量、以p為未知函數(shù)的一階微分方程（6）。若該一階微分方程能夠利用已有知識(shí)求解，則直接求出它的通解，并記為p=φ（x，C1）。

再將引入的變量p代入上述通解，就可以得到

于是，兩邊同時(shí)求不定積分，就可完成微分方程的求解

最后，引導(dǎo)學(xué)生歸納出上述方法的數(shù)學(xué)思想和關(guān)鍵步驟。顯然，上述求解過(guò)程的核心思想是“降階”，即把高階微分方程轉(zhuǎn)化為我們更加熟悉的一階微分方程。而關(guān)鍵步驟，也就是采取的核心手段是“變量代換”。事實(shí)上，變量代換是一種非常常用的轉(zhuǎn)化問(wèn)題的手段，我們?cè)谥皩W(xué)習(xí)極限的計(jì)算、導(dǎo)數(shù)的運(yùn)算和定積分的計(jì)算等內(nèi)容時(shí)常常用到。在這里，變量代換法再次發(fā)揮了重要作用，為了進(jìn)一步掌握這種方法，需要仔細(xì)分析總結(jié)這種方法的特點(diǎn)，并通過(guò)適當(dāng)練習(xí)加以鞏固。

為了幫助學(xué)生及時(shí)消化，可通過(guò)例題加以鞏固。

例1 求解

解：分析方程特點(diǎn)可以發(fā)現(xiàn)，這是一個(gè)不顯未知函數(shù)的二階微分方程，可以按照上述方法求解。

令y′=p（x），則有

將其代入原方程，得到可分離變量的微分方程

求解該方程，得到p=C1（1+x2），即

再次兩邊同時(shí)求積分，得到微分方程的通解為

至此，大約使用28分鐘將本次課的核心知識(shí)講解完畢。接下來(lái)，可通過(guò)導(dǎo)彈飛行軌跡問(wèn)題的解決，以及“降階法”的提煉，進(jìn)一步提升學(xué)員數(shù)學(xué)應(yīng)用能力和數(shù)學(xué)思維。

（五）? 回歸問(wèn)題，培養(yǎng)應(yīng)用能力

例2 導(dǎo)彈飛行軌跡問(wèn)題。

首先引導(dǎo)學(xué)員思考：根據(jù)前面的分析，雖然已經(jīng)得到了導(dǎo)彈飛行軌跡滿(mǎn)足的微分方程式（3），但由例1可知，若無(wú)其他條件，則只能求出通解，無(wú)法完全確定飛行軌跡。為此，需要找出問(wèn)題的兩個(gè)初值條件，才能求出通解中的兩個(gè)常數(shù)，從而確定特解。

首先，在初始時(shí)刻，導(dǎo)彈位于坐標(biāo)原點(diǎn)，所以當(dāng)y=0時(shí)，x=0；其次，在初始時(shí)刻，空中目標(biāo)位于點(diǎn)（3，4），而導(dǎo)彈速度方向始終指向空中目標(biāo)，所以當(dāng)x=0時(shí)，y′=4/3。再利用反函數(shù)求導(dǎo)法則，得到當(dāng)y=0時(shí)，x′=3/4。于是，得到一個(gè)含有兩個(gè)初值條件的二階微分方程

顯然，這個(gè)方程屬于不顯含未知函數(shù)x，因此可以按照上述求解方法進(jìn)行求解。

令x′=p，兩邊同時(shí)對(duì)y求導(dǎo)數(shù)，得到x″=p。

代入到原方程，轉(zhuǎn)化為

分離變量并對(duì)等式兩端同時(shí)取不定積分，得到

由初值條件x′|y=0=，解得C1=4，即

對(duì)等式左端進(jìn)行分子有理化，得到

將式（11）和式（12）兩式相加，得到

將式（13）兩端同時(shí)對(duì)y求不定積分，得到

由此，得到導(dǎo)彈運(yùn)行軌跡方程為

在問(wèn)題解決后，需要引導(dǎo)學(xué)員思考以下問(wèn)題。

一是在上述求解過(guò)程中可以看到，要想求出二階微分方程的特解，由于方程的通解中必然包含2個(gè)任意常數(shù)，因此需要利用2個(gè)初值條件來(lái)確定這2個(gè)常數(shù)的值。而在上述求解過(guò)程中，采取的是邊積分邊確定待定常數(shù)的方法，即得到式（10）后立即確定參數(shù)C2的值，得到式（14）后確定參數(shù)C1的值。事實(shí)上，在很多方程的求解過(guò)程中，邊積分邊確定常數(shù)的方法往往計(jì)算量更小。

二是在求解導(dǎo)彈追擊空中目標(biāo)的飛行軌跡時(shí)，我們是在“導(dǎo)彈始終指向空中目標(biāo)”這一假定下完成的，事實(shí)上，這是一種十分重要的導(dǎo)引律，即“尾追法”。由此可見(jiàn)，微分方程在實(shí)際問(wèn)題中有著重要應(yīng)用。當(dāng)然，隨著技術(shù)的不斷進(jìn)步，“尾追法”這種制導(dǎo)律已逐漸被更先進(jìn)的制導(dǎo)律所代替，因此需要我們持續(xù)不斷地學(xué)習(xí)，才能在未來(lái)的工作中與時(shí)俱進(jìn)，同時(shí)也鼓勵(lì)學(xué)有余力的學(xué)生查閱“精確制導(dǎo)原理”等方面的書(shū)籍資料，了解更多導(dǎo)引律及其數(shù)學(xué)原理。

三是分析上述問(wèn)題的解決過(guò)程可以發(fā)現(xiàn)，我們是先自行建立了實(shí)際問(wèn)題的數(shù)學(xué)模型，從而得到了刻畫(huà)該問(wèn)題的微分方程，才能通過(guò)求解微分方程解決該問(wèn)題。事實(shí)上，盡管我們?cè)诟叩葦?shù)學(xué)課程中，主要關(guān)注的是不同類(lèi)型微分方程的求解方法，但在許多實(shí)際問(wèn)題中，方程的建立往往比求解更為困難，甚至很多微分方程無(wú)法得到解析解。因此，為了將所學(xué)知識(shí)應(yīng)用于未來(lái)的崗位實(shí)踐中，既要始終關(guān)注和學(xué)習(xí)微分方程的建立過(guò)程，同時(shí)還要不斷學(xué)習(xí)更多的數(shù)學(xué)類(lèi)課程，如數(shù)理方程、微分方程數(shù)值解、有限元分析等。

綜上所述，對(duì)于不顯含未知函數(shù)的二階微分方程，其求解的基本思路是通過(guò)變量代換來(lái)降低微分方程的階，從而使二階微分方程轉(zhuǎn)化為兩個(gè)一階微分方程。這正是“降階法”的核心思想。在求解過(guò)程中，關(guān)鍵步驟在于令y′=p（x），即降階過(guò)程是通過(guò)變量代換來(lái)實(shí)現(xiàn)的。

四? 結(jié)束語(yǔ)

該案例以導(dǎo)彈飛行軌跡問(wèn)題為驅(qū)動(dòng)，以求解高階微分方程的降階法為核心，通過(guò)創(chuàng)設(shè)情景、提出問(wèn)題，引導(dǎo)討論、建立模型，歸納分析、引出教學(xué)內(nèi)容，分析討論、講解求解方法，回歸問(wèn)題、培養(yǎng)應(yīng)用能力等五個(gè)環(huán)節(jié)，引導(dǎo)學(xué)員由淺入深地思考，并學(xué)習(xí)如何運(yùn)用所學(xué)知識(shí)解決實(shí)際問(wèn)題。需要指出的是，所建立的微分方程式（3）是以x為未知函數(shù)的，這與我們以y為未知函數(shù)的習(xí)慣略有不同。要解決這一問(wèn)題，只需將x軸和y軸互換，并將背景設(shè)定為魚(yú)雷追擊潛艇即可。但考慮到實(shí)際中的微分方程并非必須把y視作未知函數(shù)，因此這樣設(shè)定教學(xué)案例有助于幫助學(xué)生加深對(duì)微分方程的理解。此外，采用該案例進(jìn)行教學(xué)通常比傳統(tǒng)方法多出6～8分鐘，考慮到培養(yǎng)學(xué)生數(shù)學(xué)應(yīng)用能力的需要，筆者認(rèn)為這是值得的。若條件允許，可以適當(dāng)借助翻轉(zhuǎn)課堂的方式，讓學(xué)生提前適應(yīng)案例內(nèi)容，這也是筆者下一步研究的方向。

參考文獻(xiàn)：

[1] 汪雄良，王春玲.高等數(shù)學(xué)課程研究型教學(xué)案例的構(gòu)建與實(shí)踐[J].中國(guó)教育技術(shù)裝備，2016（4）：107-109.

[2] 李坤.本科數(shù)學(xué)專(zhuān)業(yè)課程中教學(xué)案例的創(chuàng)新探索[J].大學(xué)數(shù)學(xué)，2018，34（2）：116-120.

[3] 錢(qián)明輝，李天明，舒詩(shī)雅，等.教學(xué)案例開(kāi)發(fā)框架模型的構(gòu)建及其應(yīng)用[J].管理案例研究與評(píng)論，2018，11（2）：201-220.

[4] 劉慶輝.基于常微分方程課程教學(xué)內(nèi)容改革的思考與研究[J].成都師范學(xué)院學(xué)報(bào)，2017，33（5）：115-117.

[5] 鄭蘇娟.一元微積分中探究式的教學(xué)案例[J].高等數(shù)學(xué)研究，2022，25（1）：1-3，7.