小學數學教學中滲透數學思想方法的策略

摘 要:數學思想方法是數學教學內容的重要構成,是學生必須掌握的內容,也是學生有效學習數學的助力。對此,在小學數學教學中,教師要把握教學時機,滲透數學思想方法,幫助學生掌握數學知識,獲取數學思想方法,增強數學學習效果。基于此,文章以滲透數學思想方法的時機為重點,闡述在小學數學教學中滲透數學思想方法的具體策略。
關鍵詞:小學數學;數學思想方法;滲透策略
中圖分類號:G427? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼:A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號:2097-1737(2023)28-0005-03
數學思想方法是數學思想和數學方法在數學學科的有機整合,如分類思想方法、數形結合思想方法、符號化思想方法等[1]。數學思想方法蘊含在數學知識中,是對數學知識的理性認知,具有概括性、內隱性、實用性、層次性等特點,有極強的教育價值。
在數學教學中滲透數學思想方法,可以使學生知道“從什么角度出發思考問題”和“用什么樣的數學方法解決問題”,由此掌握數學知識,同時獲取相應的思想方法,增強數學學習效果。鑒于此,教師要把握時機,在小學數學教學過程中積極地滲透數學思想方法。
一、在分析知識的過程中挖掘數學思想方法
挖掘數學思想方法是滲透數學思想方法的基礎。數學思想方法隱藏在數學知識背后。要想有效滲透數學思想方法,教師要分析數學知識,透過數學知識,挖掘其中的數學思想方法。
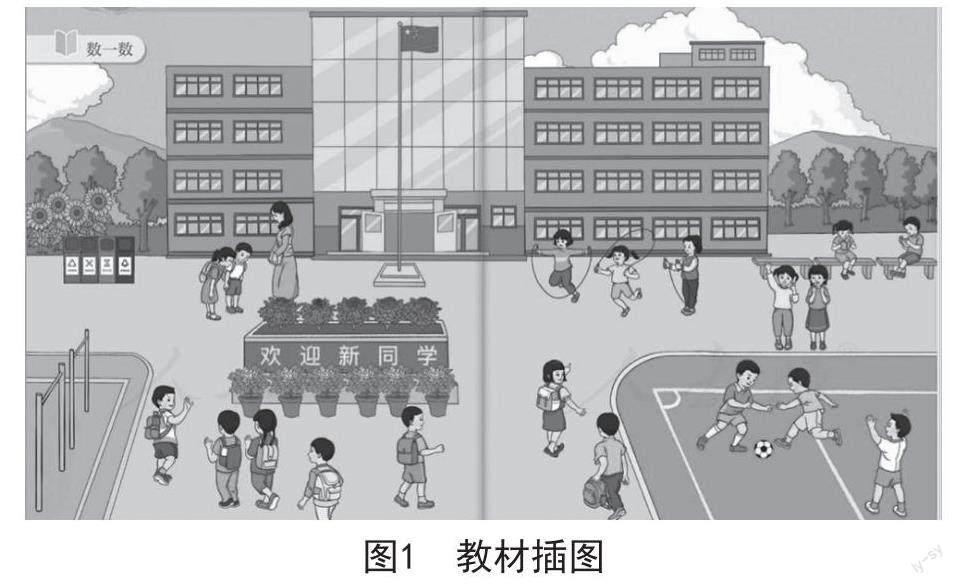
以“數一數”為例,教材在準備課的開篇呈現了以下情境圖(如圖1)。
該情境圖中蘊含著數學知識——數數。在數數的過程中,學生要做到不遺漏、不重復,這體現了數學思想方法中的對應思想。數數的過程正是學生進行統計的過程,其中蘊含了統計思想。此外,在數數的過程中,學生要將同一種事物看作整體,這就蘊含著集合思想。由此可見,“數數”這一知識點蘊含著對應思想、統計思想和集合思想。在課堂教學中,教師可以情境圖為立足點,引導學生利用不同的方式數數,以學生數數的過程為入手點,滲透不同的數學思想方法,促使學生建構相關認知。
二、在知識的發生過程中體悟數學思想方法
知識的發生過程正是數學思想方法的發生過程。數學知識的發生過程,包括數學概念的形成過程、數學規律的揭示過程等,極具層次性,蘊含著數學思想方法[2]。在此過程中滲透數學思想方法,可以使學生經歷從個別到一般、從具體到抽象、從感性到理性的認知過程,由此扎實掌握數學知識,同時獲取數學思想方法,增強數學學習效果。所以,在數學教學中,教師應把握時機滲透數學思想,引導學生體悟數學方法。
以“乘法的初步認識”為例,“幾個幾”是本節課的重點內容,也是學生理解乘法的關鍵。同時,此內容中蘊含著轉化思想和乘法意識。
基于此,在課堂上,教師先利用交互式電子白板呈現小動物活動圖片,向學生提出問題:“數一數圖片上的小動物,兔子有多少只?雞有多少只?”在此問題的驅動下,學生用不同的方法數數,最終正確數出了兔子和雞的個數。同時,學生體驗了統計思想、集合思想。然后,教師鼓勵學生暢所欲言,介紹自己數數的方法。有的學生說道:“我兩個兩個地數,數出三次,數出6只兔子;三個三個地數,數了四次,數出12只雞。”按照學生的說法,教師在黑板上寫出算式“2+2+2=6”和“3+3+3+3=12”,讓學生感受轉化思想。立足算式內容,教師發問:“這兩個算式有什么共同特點?”學生細心對比,發現算式中都是2的相加,3的相加。教師對此進行贊賞,并提出任務:“請大家拿出材料包中的圓片,將每2個擺成一堆,擺出4堆。請用加法算式進行表示,試著寫出結果。”
受到此任務的驅動,學生邊擺放邊觀察邊思考,列出算式“2+2+2+2=8”。之后,教師提出其他任務:“8個圓片,每堆擺4個,能擺幾堆?”學生們繼續操作,列出算式“4+4=8”。于是,教師在黑板上寫下兩個算式,引導學生對比。在對比的過程中,學生認真思考,
發現“2+2+2+2=4+4”。教師鼓勵學生用自己的語言進行描述。有學生描述道:“4個2相加的結果,和2個4相加的結果相同。”教師趁機引出乘法內容:“我們還可以用乘法計算4個2和2個4相加的結果。”與此同時,教師板書:2×4=8,4×2=8。基于此,教師鼓勵學生進行描述。在課堂已有認知的支撐下,學生紛紛進行描述:“2×4表示4個2相加。4×2表示2個4相加。”“2×4表示2個4相加。4×2表示4個2相加。”
通過這樣轉化數學文字語言和數學符號,學生知道了乘法的含義,加深了對所學的理解。
由此可見,引導學生經歷知識的發生過程,可以使學生一步步地掌握數學知識,同時順其自然地體悟集合思想、統計思想、轉化思想等。
三、在問題的解決過程中凸顯數學思想方法
問題解決過程是學生探究數學知識,獲取數學思想方法的過程[3]。在解決問題的過程中,學生會自覺應用數學思想方法,由此增強認知,強化問題解決能力。所以,問題解決的過程正是滲透數學思想方法的良好時機。在數學教學中,教師要依據教學內容,呈現相關問題,尤其要以問題的解決過程為時機,滲透數學思想方法。
以“雞兔同籠”為例,在課堂上,教師在交互式電子白板上出示《孫子算經》中的“雉兔同籠”問題,引導學生閱讀、思考,將其翻譯為白話文。之后,有學生復述:“籠子里有雞和兔子。從上數,雞和兔子一共有35個頭;從下數,雞和兔子一共有94只腳。雞和兔子各有多少只?”教師對此進行贊賞,并鼓勵學生進行解答。但此時,部分學生臉上露出疑惑的神色。教師把握時機,引出“化繁為簡”這一審題策略,同時呈現簡化后的問題:“籠子里有雞和兔子。雞和兔子一共有8個頭、26只腳。雞和兔子各有多少只?”在提出問題后,教師給予學生充足的時間,讓學生選用不同的方式解決問題。
在規定的時間結束后,教師組織展示活動。在活動中,有學生提到列表法:“假設有1只雞、7只兔子,此時會有30只腳,不符合題意,繼續列表,直到有3只雞、5只兔子腳數符合題意。”教師在贊賞的同時,提出問題:“如果數字變大,我們是否還能用這種方法?”
大部分學生表示否定。于是,教師鼓勵其他人介紹其他方法。此時,有學生提到畫圖法:“先畫出8個頭,在每個頭下畫出2只腳,全部表示雞。此時,一共有16只腳。與原題相比,少了10只腳,需要添加10只腳。”
在該學生介紹到此時,教師鼓勵該學生上臺畫圖。其他學生認真觀看,提出問題:“為什么不是一只一只地添加腳,而是兩只兩只地添加腳?”臺上的學生作答:
“因為一只兔子比一只雞多兩只腳,所以兩只兩只地添加。添加五次腳數就足夠了,這五次就是將5只雞換成5只兔子,也就是說有3只雞,5只兔子。”其他學生表示理解。于是,教師趁機總結解題方法,并揭露其中蘊含的數學思想方法——數形結合法。之后,教師按照此方式,引導其他學生繼續展現其他解題方法。
實踐證明,學生通過體驗問題解決活動,積極思維,解決了問題,建構了數學認知,尤其掌握了不同的解題方法。同時,學生也感受到了不同方法中蘊含的數學思想和方法,有利于提高問題解決水平。
四、在知識的總結過程中歸納數學思想方法
知識總結過程既是學生總結數學知識點的過程,又是學生歸納數學思想方法的過程[4]。在數學課堂上,學生通過體驗多樣活動,不但掌握了數學知識點,還習得了數學思想方法。在課堂總結環節,教師要立足學生的學習情況,提出總結任務,促使學生回顧課堂學習過程、歸納知識點和數學思想方法,達到查缺補漏、建構完善認知、增強課堂學習效果的目的。
以“三角形的分類”為例,本課涉及分類思想。立足于此,在課堂上,教師組織分類活動,引導學生與小組成員合作,從不同的角度對三角形進行分類。在此過程中,大部分小組從邊和角入手,對三角形進行分類,了解了直角三角形、等腰三角形和等邊三角形,同時獲取了分類思想。于是,在課堂總結環節,教師提出如下任務:“請大家回顧課堂學習內容,利用韋恩圖,對三角形進行分類,展現三角形的分類結果。”在此任務的驅動下,學生積極進行頭腦風暴,在腦海中呈現出三角形分類的全過程,由此了解不同的三角形及關系。之后,學生發散思維,依照邊和角對三角形進行分類,呈現出不同的圖像。實際上,學生繪圖的過程,正是學生轉化分類思想的過程。在此過程中,學生會增強對分類思想的認知。
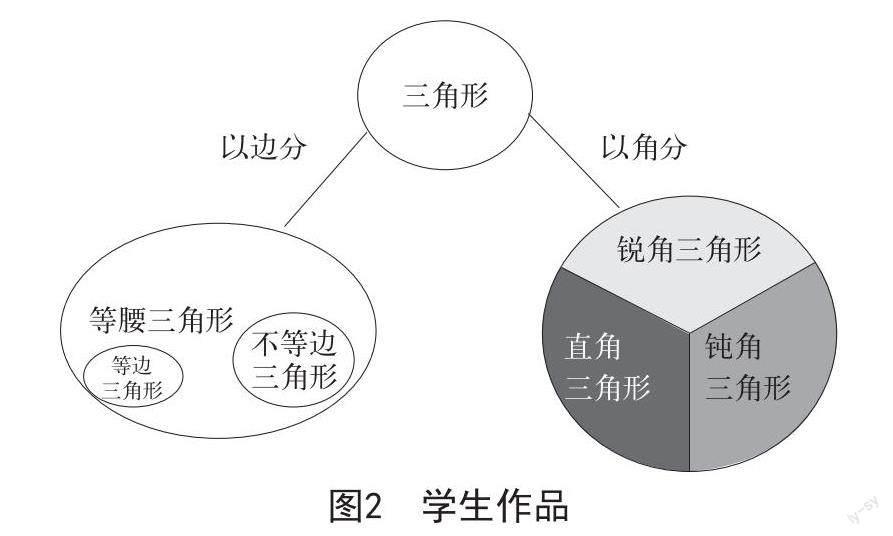
在學生做出圖像后,教師隨機選擇一幅作品(如圖2),并鼓勵學生代表依據圖像內容,介紹三角形的分類依據和結果。
學生代表介紹之后,其他學生提出問題,如“等腰三角形和不等邊三角形之間是否存在關系?存在怎樣的關系?”“等邊三角形是特殊的等腰三角形嗎?”等。學生代表面對一個個問題認真作答,同時借此完善自己的圖像內容,以增強認知能力。
如此做法,不但使學生應用了數學思想方法,梳理了數學知識點,加深了對數學知識的理解,還使學生順其自然地歸納了數學思想方法,增強了對數學思想方法的認知。
五、在知識的運用過程中使用數學思想方法
學生運用數學思想方法是滲透數學思想的重要目的,知識的應用過程是學生使用數學思想方法的過程[5],
而課堂練習、課后作業是學生應用數學知識的主陣地。在數學教學中,教師應以知識的應用為抓手,聯系學生的學習所得設計相關習題,由此組織課堂練習活動和課后作業活動,促使學生遷移已有認知,用數學思想方法解答習題。
以“集合”為例,學生在課堂上體驗情境活動,感知了集合圈的形成過程,感受了集合思想。但是,學生受到學習差異影響,學習水平不盡相同。于是,教師立足教學內容和學生學習差異,分層設計習題,使每個學生都有運用數學思想方法的機會。教師具體設計了如下習題:
1.某班有30人訂閱語文報紙,26人訂閱數學報紙,8人訂閱兩種報紙,一共有( )人訂閱了報紙。
2.某年級有108人報名參加春游活動。其中,65人帶了礦泉水,63人帶了水果,每人至少帶一種。那么,既帶了礦泉水,又帶了水果的有( )人。
3.學校開設了兩個社團。39人報名參加體育社團,43人報名參加音樂社團,7人同時報名參加兩個社團,一共有( )人參加社團活動。
學生依據自身學情,自選相應難度的題目。在解決習題時,學生遷移集合思想方法,解決相關問題,由此強化集合思想,鍛煉問題解決能力。
六、結束語
綜上所述,有效滲透數學思想方法于數學教學,可以使學生掌握數學知識,獲取數學思想方法,提高數學學習水平。所以,教師在小學數學教學中可以依據數學教學內容,把握教學時機,運用多樣策略,滲透數學思想方法,引導學生經歷數學原理推導過程、數學問題解決過程、數學知識總結過程和數學知識應用過程,進而扎實掌握數學知識,獲取數學思想方法,提升數學學習質量。
參考文獻
馬芳.在小學數學教學中滲透數學思想方法的有效路徑探討[J].數學學習與研究,2021(34):143-145.
仁欠吉.淺談數學思想方法在小學數學教學中的滲透[J].科幻畫報,2021(9):91-92.
張彥紅.小學數學教學中滲透數學思想方法的思考[J].智力,2021(18):70-71.
徐士波.在小學數學教學中滲透數學思想方法的有效路徑探討[J].讀寫算,2020(36):187-188.
胡愛霞.小學數學教學中數學思想方法的滲透[J].試題與研究,2020(28):152-153.
基金項目:本文系福建省福州市長樂區教育科學研究2021年度課題“小學數學教學中滲透數學思想方法的實踐研究”(課題編號:CJXK2021026)的研究成果。
作者簡介:歐陽燕平(1979.2-),女,福建福州人,任教于福建省福州市長樂區漳港中心小學,一級教師,本科學歷,曾榮獲“福州市優秀教育工作者”稱號。

