多角度思考關注數(shù)學本質以提升核心素養(yǎng)


摘 要:文章通過從不同角度對2023年新高考Ⅱ卷的立體幾何試題進行分析,反觀教材,反思教學,培養(yǎng)學生的邏輯推理、直觀想象、數(shù)學運算核心素養(yǎng).
關鍵詞:核心素養(yǎng);邏輯推理;直觀想象;數(shù)學運算;反思教學
中圖分類號:G632 文獻標識碼:A 文章編號:1008-0333(2023)31-0044-03
收稿日期:2023-08-05
作者簡介:吳瑞瑞(1983.7-),女,安徽省濉溪人,碩士,中學一級教師,從事高中數(shù)學教學研究.
2023年高考試題突出強調對基礎知識、基本概念的深入理解和靈活掌握,注重考查學科知識的綜合應用能力,落實中國高考評價體系中“四翼”的考查要求,助力“雙減”政策落地.同時,合理控制試題難度,科學引導中學教學,力圖促進高中教學與義務教育階段學習的有效銜接.立體幾何是培養(yǎng)學生邏輯推理、數(shù)學運算、直觀想象學科核心素養(yǎng)的一個很好的載體,本文以2023年新高考Ⅱ卷的立體幾何試題為例,從不同角度對解法進行分析,以期為老師的教學,學生的學習提供可借鑒的方法和思路.
1 試題再現(xiàn)
2 試題解析
分析 第(1)問要證明的是異面直線垂直,常用到的方法是證明線面垂直以達到證明線線垂直的目的,或把異面直線問題轉化為共面直線問題,體現(xiàn)降維思想.再利用三角形的有關知識解決,或者利用基底法證明向量數(shù)量積為0,也可以選擇特殊的基底,比如常用到的坐標法也就是選擇單位正交基底來進行解決.
第(2)問求二面角的正弦值,可以采用傳統(tǒng)幾何法找到二面角,然后解三角形;也可以采用向量法,利用選擇的基底表示面的法向量;也可采用坐標法(特殊的基底),找面的法向量或者是找到垂直于交線的兩個向量,進而求出二面角的正弦值[1].
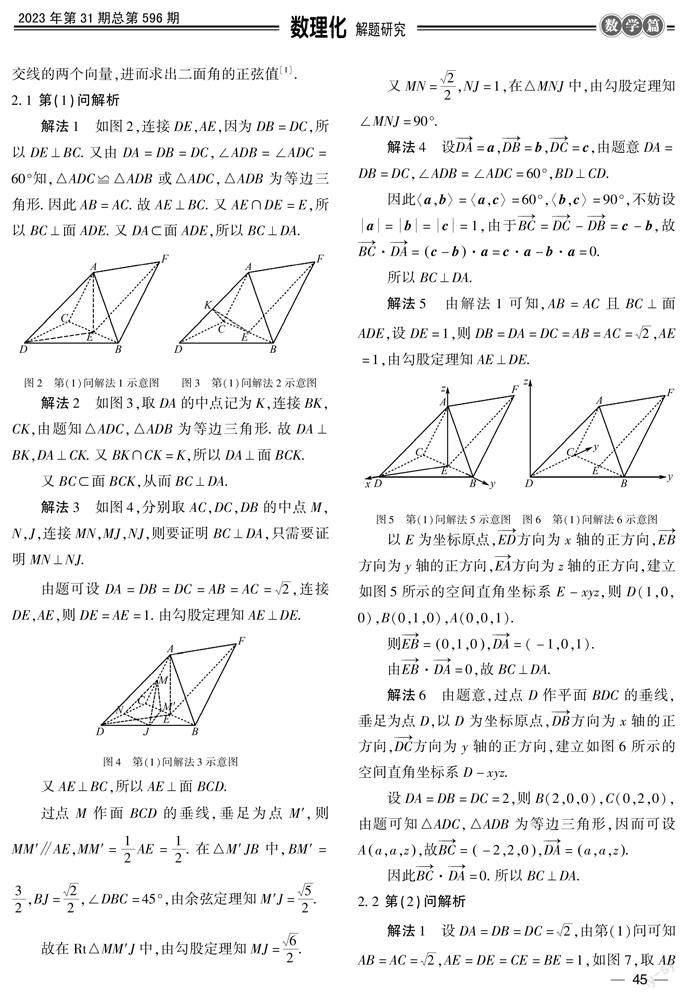
2.1 第(1)問解析
2.2 第(2)問解析
不少老師發(fā)聲說,新教材更加重視空間向量,而且對于線面角、面面角的問題,學生幾乎全部選擇建系處理,那么傳統(tǒng)幾何法和向量法更應側重哪一個?章建躍主編曾給予回復說,無論是向量法還是幾何法,我們都要用幾何眼光去觀察圖形,然后才是用向量法解決,對象還是幾何對象,需要了解幾何對象結構的基本關系,如果不了解幾何對象,是無法運用向量法的,如果不熟悉空間結構就無法建系.也就是說對于立體幾何問題的解決,先是直觀想象和邏輯推理能力的考查,再選用向量這個有利工具去程序化地解決問題.
參考文獻:
[1]
周宗杰,牛松.北師大版高中數(shù)學必修2教材中例題解答對學生的誤導分析:以2019年高考數(shù)學全國卷Ⅰ理科第18題(1)為例[J].中國數(shù)學教學,2019(5):12-15.
[責任編輯:李 璟]

