基于雨課堂混合式教學(xué)模式的工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)研究

何敬民

摘? 要：該文基于雨課堂混合式教學(xué)模式的工程數(shù)學(xué)教學(xué)數(shù)據(jù)，構(gòu)建教學(xué)質(zhì)量評(píng)價(jià)體系。首先，從雨課堂教學(xué)數(shù)據(jù)中提取出對教學(xué)質(zhì)量有重大影響的五個(gè)因素，即課件預(yù)習(xí)率、到課率、課堂答題得分率、課后作業(yè)和期中考試成績。其次，以期末考試成績作為課程教學(xué)質(zhì)量的目標(biāo)，建立單因素線性回歸模型和多因素線性回歸模型。結(jié)果表明每個(gè)因素對期末考試成績的影響都顯著，但在多因素分析中，預(yù)習(xí)率、課后作業(yè)對期末考試成績的影響顯著，其中課后作業(yè)占比最大，貢獻(xiàn)最高。最后，利用統(tǒng)計(jì)回歸模型預(yù)測期末考試成績，對學(xué)生實(shí)施精準(zhǔn)教學(xué)。該方法可為工程數(shù)學(xué)高效、準(zhǔn)確的教學(xué)質(zhì)量評(píng)價(jià)提供借鑒和參考，推動(dòng)智能化教學(xué)質(zhì)量評(píng)價(jià)體系的建立。

關(guān)鍵詞：工程數(shù)學(xué)；混合式教學(xué)模式；教學(xué)質(zhì)量評(píng)價(jià)；線性回歸；雨課堂

中圖分類號(hào)：G642? ? ? 文獻(xiàn)標(biāo)志碼：A? ? ? ? ? 文章編號(hào)：2096-000X（2024）11-0072-04

Abstract： Based on the teaching data of Engineering Mathematics in the mixed teaching mode of rain classroom， this paper constructs the teaching quality evaluation system. Firstly， five factors which have great influence on teaching quality are extracted from the teaching data of rain classroom： courseware preview rate， class attendance rate， score rate for class questions， homework after class and mid-term exam score. Secondly， taking the final exam score as the goal of course teaching quality， the single factor linear regression model and the multi-factor linear regression model are established. The results show that each factor has a significant impact on the final exam score， but in the multi-factor analysis， the preview rate and homework after class have a significant impact on the final exam score， among which homework after class accounts for the largest proportion and the highest contribution. Finally， the statistical regression model is used to predict the final exam scores and implement precision teaching for students. This method can provide reference and guidance for efficient and accurate teaching quality evaluation of engineering mathematics， and promote the establishment of intelligent teaching quality evaluation system.

Keywords： Engineering Mathematics; mixed teaching mode; teaching quality evaluation; linear regression; rain classroom

隨著“互聯(lián)網(wǎng)+”教育的深度發(fā)展，線上教學(xué)、線下教學(xué)、線上線下混合式教學(xué)已成為高等教育的一種發(fā)展趨勢。各類大、中專院校紛紛進(jìn)行教學(xué)改革，教學(xué)模式和教學(xué)平臺(tái)如雨后春筍般應(yīng)運(yùn)而生，不僅老師們紛紛嘗試不同的教學(xué)模式和教學(xué)手段，專家學(xué)者們也紛紛從教學(xué)模式、教學(xué)手段、教學(xué)過程對教學(xué)進(jìn)行研究。李海東等[1]以國家級(jí)線上線下混合式一流課程為實(shí)踐樣本，構(gòu)建了混合式教學(xué)質(zhì)量評(píng)價(jià)模型。牛富榮[2]給出了翻轉(zhuǎn)課堂教學(xué)質(zhì)量評(píng)價(jià)的設(shè)計(jì)理念、設(shè)計(jì)思路和設(shè)計(jì)指標(biāo)。隋欣[3]基于雨課堂的教學(xué)數(shù)據(jù)，設(shè)計(jì)了雨課堂信息化教學(xué)評(píng)價(jià)體系。朱亞輝[4]以概率論與數(shù)理統(tǒng)計(jì)為例，通過問卷調(diào)查分析和期末成績統(tǒng)計(jì)指標(biāo)評(píng)價(jià)雨課堂教學(xué)模式的教學(xué)效果。宋麗雅[5]基于灰色關(guān)聯(lián)分析，構(gòu)建了用于評(píng)估高職院校數(shù)學(xué)教學(xué)質(zhì)量的評(píng)價(jià)系統(tǒng)。王楊[6]構(gòu)建了雨課堂混合式教學(xué)模式，并對模式的實(shí)施過程、考核方式、教學(xué)效果和教學(xué)模式評(píng)價(jià)進(jìn)行深入的研究。胡藝芹等[7]基于層次分析法建立了公共英語翻轉(zhuǎn)課堂的教學(xué)評(píng)價(jià)體系。劉文彬等[8]提出了一種基于學(xué)生學(xué)習(xí)行為數(shù)據(jù)的在線課程教學(xué)質(zhì)量評(píng)價(jià)方法。林廣利等[9]對雨課堂的教學(xué)實(shí)踐效果進(jìn)行了綜合評(píng)價(jià)研究，并據(jù)此構(gòu)建了指標(biāo)評(píng)價(jià)體系。朱亞紅等[10]從診斷性評(píng)價(jià)、形成性評(píng)價(jià)以及終結(jié)性評(píng)價(jià)三個(gè)方面詳細(xì)闡述評(píng)價(jià)方案。隨著雨課堂、智慧樹、課堂派等教學(xué)平臺(tái)引入，教學(xué)數(shù)據(jù)的獲得成為了可能。隨著從教學(xué)平臺(tái)獲得教學(xué)數(shù)據(jù)越來越豐富，許多統(tǒng)計(jì)方法開始運(yùn)用到教學(xué)質(zhì)量評(píng)價(jià)之中，使得教學(xué)評(píng)價(jià)更加客觀。岳琪等[11]提出了一種基于遺傳算法和BP神經(jīng)網(wǎng)絡(luò)的教學(xué)質(zhì)量評(píng)價(jià)模型。甄穎等[12]運(yùn)用主成分分析法建立了高等數(shù)學(xué)線上線下教學(xué)質(zhì)量評(píng)價(jià)模型。李可心等[13]提出了一種基于SOM神經(jīng)網(wǎng)絡(luò)的工程經(jīng)濟(jì)學(xué)教學(xué)質(zhì)量評(píng)價(jià)模型。李瑋玲[14]利用主成分分析法建立高等數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)模型，并運(yùn)用數(shù)據(jù)對高等數(shù)學(xué)教學(xué)質(zhì)量進(jìn)行實(shí)證檢驗(yàn)。張敏[15]利用馬爾可夫鏈研究了探究式教學(xué)模式的效果。喻朝陽[16]提出了一種由層次分析法、主成分分析法和支持向量機(jī)組合的高等數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)模型。努爾古麗·艾力等[17]用統(tǒng)計(jì)分析的方法對高等數(shù)學(xué)進(jìn)行教學(xué)質(zhì)量分析評(píng)價(jià)。

一? 工程數(shù)學(xué)的教學(xué)現(xiàn)狀

工程數(shù)學(xué)包括線性代數(shù)、概率論與數(shù)理統(tǒng)計(jì)、復(fù)變函數(shù)與積分變換、場論與數(shù)理方程等學(xué)科，是一些理論性和應(yīng)用性都很強(qiáng)的學(xué)科。工程數(shù)學(xué)是工科院校培養(yǎng)高素質(zhì)應(yīng)用型人才開設(shè)的必修課，傳統(tǒng)的課程考核評(píng)價(jià)是根據(jù)平時(shí)成績和期末卷面考試成績按照一定的比例進(jìn)行加權(quán)平均得出該門課程的總評(píng)成績。平時(shí)成績只依賴于任課教師掌握學(xué)生的出勤、完成作業(yè)等情況給出，考核評(píng)價(jià)方式過于單一。每所工科院校中工程數(shù)學(xué)學(xué)習(xí)的人數(shù)較多，而每個(gè)任課教師平時(shí)成績評(píng)價(jià)的標(biāo)準(zhǔn)不統(tǒng)一，導(dǎo)致全校學(xué)生的課程排名不盡公平、合理，從而影響后期學(xué)生的選專業(yè)和保研。傳統(tǒng)的工程數(shù)學(xué)教學(xué)以期末卷面成績衡量學(xué)生的學(xué)習(xí)效果，完全忽略形成性評(píng)價(jià)和學(xué)生的學(xué)習(xí)過程，不能實(shí)時(shí)掌握學(xué)生的學(xué)習(xí)情況，缺乏過程性評(píng)價(jià)。

隨著在線教學(xué)資源的建設(shè)和智能化教學(xué)平臺(tái)引入，在線學(xué)習(xí)和移動(dòng)學(xué)習(xí)成為高校教育的一種發(fā)展趨勢，各大高校紛紛進(jìn)行課堂教學(xué)改革，線上線下混合式教學(xué)應(yīng)運(yùn)而生。天津理工大學(xué)走在課堂教學(xué)改革的前列，引進(jìn)了雨課堂、智慧樹等教學(xué)平臺(tái)，老師們也紛紛嘗試線上線下混合式教學(xué)模式。在新的教學(xué)模式下，傳統(tǒng)的教學(xué)評(píng)價(jià)不能適應(yīng)時(shí)代的發(fā)展，急需一個(gè)全新的教學(xué)質(zhì)量評(píng)價(jià)體系。鑒于此，本文主要探尋基于雨課堂混合式教學(xué)模式的工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)。

二? 工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)體系的構(gòu)建

筆者采用雨課堂進(jìn)行工程數(shù)學(xué)的線上線下混合式教學(xué)，課前推送課程課件和課程視頻預(yù)習(xí)，課堂上講解知識(shí)點(diǎn)和推送習(xí)題進(jìn)行答題，課后推送課后作業(yè)驗(yàn)證教學(xué)效果。雨課堂可以獲得的數(shù)據(jù)有課前預(yù)習(xí)課程課件和課程視頻的觀看頁數(shù)、課堂上的簽到次數(shù)和答題的得分、課后作業(yè)的情況，另外還能獲得班級(jí)的期中考試成績和期末考試成績。我們把學(xué)生期末考試成績作為學(xué)生本門課程學(xué)習(xí)質(zhì)量的唯一標(biāo)準(zhǔn)，探尋期末考試成績與預(yù)習(xí)課件和視頻頁數(shù)、課堂簽到次數(shù)、課堂答題得分、課后作業(yè)和期中考試成績的關(guān)系。數(shù)據(jù)來源于筆者所教某一門工程數(shù)學(xué)課程某一班級(jí)的課堂數(shù)據(jù)，樣本數(shù)為151份。

（一）? 數(shù)據(jù)預(yù)處理

為了消除數(shù)據(jù)的大小和量綱對數(shù)據(jù)結(jié)果的影響，我們先對數(shù)據(jù)進(jìn)行預(yù)處理。用學(xué)生預(yù)習(xí)觀看頁數(shù)除以觀看總頁數(shù)，稱為預(yù)習(xí)率，記為X1；用學(xué)生課堂簽到次數(shù)除以簽到總次數(shù)，稱為到課率，記為X2；用學(xué)生課堂答題得分除以課堂答題總分，稱為答題得分率，記為X3。課后作業(yè)按優(yōu)（4分）、良（3分）、中（2分）、差（1分）、不交（0分）給分后取平均值，然后對平均得分進(jìn)行0-1標(biāo)準(zhǔn)化處理，處理后的數(shù)據(jù)記為X4。對期中考試成績和期末考試成績進(jìn)行0-1標(biāo)準(zhǔn)化處理，處理后的數(shù)據(jù)分別記為X5和Y。下面主要考慮因變量Y與自變量X1，X2，…，X5之間的關(guān)系，自變量對因變量的影響。

（二）? 單因素線性回歸分析

為了研究預(yù)習(xí)率、到課率、答題得分率、課后作業(yè)、期中考試成績對期末考試成績的影響，我們先研究各個(gè)因素對期末考試成績的影響。首先分別建立各個(gè)自變量對因變量的線性回歸，模型如下

從表1的計(jì)算結(jié)果可以看出每個(gè)變量的p值都小于0.05，F(xiàn)值都大于F臨界值，說明預(yù)習(xí)率、到課率、答題得分率、課后作業(yè)、期中考試成績對期末考試成績的影響都顯著，其中課后作業(yè)的貢獻(xiàn)率為58.16%，預(yù)習(xí)率的貢獻(xiàn)率為20.81%，答題得分率的貢獻(xiàn)率為19.49%，到課率的貢獻(xiàn)率為7.22%，期中考試成績的貢獻(xiàn)率為3.44%。從課堂教學(xué)數(shù)據(jù)來看，預(yù)習(xí)率、答題得分率和課后作業(yè)對期末考試成績的影響最大，應(yīng)該在教學(xué)過程中加強(qiáng)課前預(yù)習(xí)、課堂答題、課后作業(yè)的嚴(yán)格管理和監(jiān)督。

（三）? 多因素線性回歸分析

為了研究預(yù)習(xí)率、到課率、答題得分率、課后作業(yè)、期中考試成績多個(gè)變量對期末考試成績的整體影響，我們建立多變量線性回歸模型

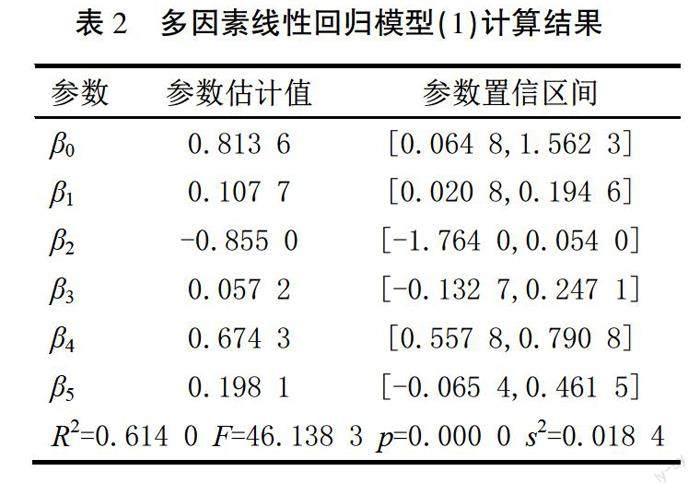
從表2的計(jì)算結(jié)果可以看出p值小于0.05，F(xiàn)值大于F臨界值，說明模型從整體上看成立。參數(shù)？茁2，？茁3，？茁5的置信區(qū)間包含零點(diǎn)，說明到課率、答題得分率、期中考試成績對期末考試成績的影響不太顯著。去掉不顯著的因素，重新建立線性回歸模型

從表3的計(jì)算結(jié)果看p值小于0.05，F(xiàn)值遠(yuǎn)大于F臨界值，說明模型整體上可用，期末考試成績的60.38%可由模型解釋。而由圖1殘差分布圖可知，有15個(gè)數(shù)據(jù)點(diǎn)的殘差置信區(qū)間不包含零點(diǎn)，數(shù)據(jù)應(yīng)視為異常點(diǎn)，將其剔除后重新運(yùn)行程序計(jì)算，回歸參數(shù)及其置信區(qū)間、檢驗(yàn)統(tǒng)計(jì)量R2，F(xiàn)，p，s2的計(jì)算結(jié)果見表4。

從表4的計(jì)算結(jié)果看，回歸參數(shù)k0、k1、k2變化度不大，參數(shù)的置信區(qū)間長度變短，R2值和F值變大，殘差平方和s2變小，說明修正后的模型更加可信，期末考試成績的78.59%可由模型解釋。在單因素線性回歸分析中，預(yù)習(xí)率、到課率、答題得分率、課后作業(yè)、期中考試成績對期末考試成績的影響都顯著，但在多因素線性回歸分析中，預(yù)習(xí)率、課后作業(yè)對期末考試成績的影響顯著，課后作業(yè)占比最大，貢獻(xiàn)最高。由回歸模型可知，到課率、答題得分率、課后作業(yè)、期中考試成績存在多重共線性，課后作業(yè)可以高度反映到課率、答題得分率和期中考試成績。

（四）? 期末考試成績預(yù)測

由多因素線性回歸分析可知，期末考試成績的回歸預(yù)測模型為

由期末考試成績的回歸預(yù)測模型可以看出，課后作業(yè)的權(quán)重較大，課后作業(yè)的得分對期末考試成績的影響較大，預(yù)習(xí)率的權(quán)重較小，預(yù)習(xí)率對期末考試成績的影響較小。若能提高學(xué)生的預(yù)習(xí)率和課后作業(yè)情況，就能提高學(xué)生的期末考試成績。通過回歸預(yù)測模型，根據(jù)學(xué)生的課堂表現(xiàn)，就能估計(jì)出學(xué)生的期末考試成績和期末考試成績的置信區(qū)間，對學(xué)生分段實(shí)施精準(zhǔn)教學(xué)。在教學(xué)中，若能抓住課前預(yù)習(xí)和課后作業(yè)兩大關(guān)鍵因素，就能提高學(xué)生的學(xué)習(xí)成績。課前預(yù)習(xí)反映了學(xué)生課前學(xué)習(xí)的情況，課后作業(yè)的質(zhì)量反映了學(xué)生課上學(xué)習(xí)的掌握程度，老師們?nèi)裟芏酱賹W(xué)生的預(yù)習(xí)和課后作業(yè)的完成質(zhì)量，就能提高學(xué)生的期末考試成績。

三? 工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)結(jié)果的運(yùn)用

工程教學(xué)教學(xué)質(zhì)量評(píng)價(jià)體系揭示出大學(xué)生知識(shí)掌握情況與雨課堂教學(xué)數(shù)據(jù)中各個(gè)因素之間的內(nèi)在規(guī)律，從數(shù)量指標(biāo)上給出了當(dāng)今大學(xué)生知識(shí)掌握情況與教學(xué)各個(gè)因素之間的關(guān)系。筆者已將工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)體系融入工程數(shù)學(xué)的教學(xué)之中，分章進(jìn)行階段性測驗(yàn)，以階段性測驗(yàn)的成績作為評(píng)判本門課程教學(xué)質(zhì)量的唯一標(biāo)準(zhǔn)，尋求課程教學(xué)質(zhì)量與預(yù)習(xí)課件和視頻頁數(shù)、課堂簽到次數(shù)、課堂答題得分和課后作業(yè)的關(guān)系，及時(shí)調(diào)整回歸系數(shù)。用雨課堂即時(shí)教學(xué)數(shù)據(jù)預(yù)測學(xué)生的學(xué)習(xí)成績及其區(qū)間估計(jì)，對學(xué)生實(shí)施精準(zhǔn)教學(xué)，并且已經(jīng)取得了良好的效果。授課教師可以根據(jù)即時(shí)的雨課堂教學(xué)數(shù)據(jù)，及時(shí)采取教學(xué)措施，調(diào)整授課內(nèi)容和授課方法，提高大學(xué)生的知識(shí)結(jié)構(gòu)和培養(yǎng)質(zhì)量。工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)體系一切從雨課堂教學(xué)數(shù)據(jù)中來，到雨課堂教學(xué)中去，具有數(shù)學(xué)建模“始于實(shí)踐，終于實(shí)踐”的特點(diǎn)，評(píng)價(jià)體系更加客觀。實(shí)踐證明，在工程數(shù)學(xué)的教學(xué)過程中，工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)體系可以為授課教師評(píng)價(jià)授課內(nèi)容的掌握程度提供理論根據(jù)，實(shí)現(xiàn)工程數(shù)學(xué)高效、精準(zhǔn)教學(xué)，為推動(dòng)智能化教學(xué)質(zhì)量評(píng)價(jià)體系的構(gòu)建提供借鑒和參考。

四? 結(jié)論

隨著現(xiàn)代信息技術(shù)與教育教學(xué)的深度融合，線上線下混合式教學(xué)已成為高校教育的一種發(fā)展趨勢。筆者基于雨課堂教學(xué)平臺(tái)，對工程數(shù)學(xué)實(shí)施線上線下混合式教學(xué)。雨課堂可以獲得對教學(xué)質(zhì)量有重大影響的五個(gè)因素：課件和課程視頻預(yù)習(xí)率、到課率、課堂答題得分率、課后作業(yè)和期中考試成績。我們把期末考試成績作為評(píng)價(jià)教學(xué)質(zhì)量的唯一標(biāo)準(zhǔn)，微觀探尋各個(gè)因素與教學(xué)質(zhì)量的關(guān)系，構(gòu)建工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)模型。在單因素線性回歸分析中，發(fā)現(xiàn)各個(gè)教學(xué)因素對教學(xué)質(zhì)量的影響都顯著，但在多因素線性回歸分析中，預(yù)習(xí)率和課后作業(yè)對教學(xué)質(zhì)量的影響顯著，其中課后作業(yè)占比最大，貢獻(xiàn)最高。進(jìn)而利用回歸預(yù)測模型預(yù)測學(xué)生的考試成績，對學(xué)生實(shí)施精準(zhǔn)教學(xué)。筆者已將工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)模型應(yīng)用到工程數(shù)學(xué)的教學(xué)之中，開展即時(shí)評(píng)價(jià)。工程數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)模型可實(shí)現(xiàn)工程數(shù)學(xué)高效、精準(zhǔn)的教學(xué)質(zhì)量評(píng)價(jià)，為推動(dòng)智能化教學(xué)質(zhì)量評(píng)價(jià)體系的建立提供借鑒和參考。

參考文獻(xiàn)：

[1] 李海東，吳昊.基于全過程的混合式教學(xué)質(zhì)量評(píng)價(jià)體系研

究——以國家級(jí)線上線下混合式一流課程為例[J].中國大學(xué)教學(xué)，2021，2021（5）：65-71，91.

[2] 牛富榮.財(cái)政學(xué)翻轉(zhuǎn)課堂教學(xué)質(zhì)量評(píng)價(jià)體系的構(gòu)建[J].山西財(cái)經(jīng)大學(xué)學(xué)報(bào)，2020，42（S2）：125-128.

[3] 隋欣.基于雨課堂的高職院校信息化教學(xué)評(píng)價(jià)體系探究[J].黑龍江科學(xué)，2020，11（5）：52-53.

[4] 朱亞輝.基于雨課堂教學(xué)模式的教學(xué)效果評(píng)價(jià)——以《概率論與數(shù)理統(tǒng)計(jì)》為例[J].電腦知識(shí)與技術(shù)，2020，16（31）：162-163.

[5] 宋麗雅.基于灰色關(guān)聯(lián)分析的高職院校數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)系統(tǒng)設(shè)計(jì)[J].廣州城市職業(yè)學(xué)院學(xué)報(bào)，2021，15（4）：35-38.

[6] 王楊.基于“雨課堂”項(xiàng)目化課程混合式教學(xué)的效果與評(píng)價(jià)[J].職教論壇，2020，2020（2）：70-75.

[7] 胡藝芹，張?jiān)魄?基于層次分析法的公共英語翻轉(zhuǎn)課堂教學(xué)評(píng)價(jià)指標(biāo)體系研究[J].蘭州教育學(xué)院學(xué)報(bào)，2017，33（10）：133-137，146.

[8] 劉文彬，楊波，屈喜龍.基于學(xué)習(xí)行為數(shù)據(jù)的在線課程教學(xué)質(zhì)量精準(zhǔn)評(píng)價(jià)方法[J].湖南工程學(xué)院學(xué)報(bào)（自然科學(xué)版），2022，32（3）：49-55.

[9] 林廣利，宮秀濱，苑宏憲，等.雨課堂教學(xué)實(shí)踐效果評(píng)價(jià)研究[J].長春教育學(xué)院學(xué)報(bào)，2019，35（11）：58-61，64.

[10] 朱亞紅，曹繼平，吳聰偉.面向軍事應(yīng)用和專業(yè)學(xué)習(xí)的《工程數(shù)學(xué)》例證教學(xué)評(píng)價(jià)方法研究[J].教育教學(xué)論壇，2019，2019

（28）：149-150.

[11] 岳琪，溫新.基于GA和BP神經(jīng)網(wǎng)絡(luò)的教學(xué)質(zhì)量評(píng)價(jià)模型研究[J].內(nèi)蒙古大學(xué)學(xué)報(bào)（自然科學(xué)版），2018，49（2）：204-211.

[12] 甄穎，許寧寧，李庚，等.基于PCA的高等數(shù)學(xué)線上線下教學(xué)質(zhì)量評(píng)價(jià)模型：以天津工業(yè)大學(xué)為例[J].首都師范大學(xué)學(xué)報(bào)（自然科學(xué)版），2022，43（5）：59-64.

[13] 李可心，張斌，蒙彥宇，等.基于SOM神經(jīng)網(wǎng)絡(luò)的工程經(jīng)濟(jì)學(xué)教學(xué)質(zhì)量評(píng)價(jià)模型研究[J].現(xiàn)代電子技術(shù)，2023，46（18）：162-166.

[14] 李瑋玲.基于主成分分析的高等數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)模型[J].河西學(xué)院學(xué)報(bào)，2011，27（5）：90-94.

[15] 張敏.齊次Markov鏈在高等數(shù)學(xué)教學(xué)質(zhì)量的評(píng)價(jià)中的應(yīng)用[J].數(shù)理醫(yī)藥學(xué)雜志，2013，26（4）：495-497．

[16] 喻朝陽.AHP-PCA-SVM的高等數(shù)學(xué)教學(xué)質(zhì)量評(píng)價(jià)[J].科技通報(bào)，2013，29（10）：229-231.

[17] 努爾古麗·艾力，張艷，張瑜.基于統(tǒng)計(jì)分析的教學(xué)質(zhì)量的分析評(píng)價(jià)——以高等數(shù)學(xué)教學(xué)為例[J].南昌教育學(xué)院學(xué)報(bào)，2012，27（5）：54-55.