基于主動學習與貝葉斯深度神經網絡的高維多輸出不確定性傳播方法

2024-06-06 16:40:22劉竟飛姜潮倪冰雨汪宗太

中國機械工程 2024年5期

劉竟飛姜潮倪冰雨汪宗太

摘要：

針對實際工程中存在的具有多個輸出響應的高維問題，提出一種基于主動學習與貝葉斯深度神經網絡的高維多輸出不確定性傳播方法。利用多個輸出響應對應同一組輸入變量的特點，對輸入變量進行一次性采樣，從而構造初始訓練樣本集。采用貝葉斯深度神經網絡初步構建高維多輸出問題的代理模型。貝葉斯深度神經網絡能夠同時求解多個預測輸出響應的不確定性估計，基于該特點發展了一種針對高維多輸出問題的主動加點策略，通過主動學習的方式進一步構建具有較高精度的高維多輸出代理模型。然后，利用蒙特卡羅采樣方法以及高斯混合模型求解多個輸出響應的聯合概率密度函數。研究結果表明，所提方法不僅能夠避免分別對多個輸出響應進行獨立求解的復雜過程，而且能夠利用多個輸出響應之間的關聯，主動篩選關鍵樣本點進行建模，在一定程度上提高了高維多輸出問題的求解效率。最后，通過幾個數值算例驗證了所提方法的有效性。

關鍵詞：主動學習；貝葉斯深度神經網絡；高維不確定性；多輸出問題

中圖分類號：TP182

DOI：10.3969/j.issn.1004132X.2024.05.004

開放科學（資源服務）標識碼（OSID）：

High Dimensional Multioutput Uncertainty Propagation Method

via Active Learning and Bayesian Deep Neural Network

LIU Jingfei1? JIANG Chao2? NI Bingyu2? WANG Zongtai3

1.School of Mechanical and Electrical Engineering，Henan University of Technology，

Zhengzhou，450001

2.School of Mechanical and Vehicle Engineering，Hunan University，Changsha，410082

3.China Nuclear Power Engineering Co.，Ltd.，Beijing，100048

Abstract： An uncertainty propagation method was proposed based on active learning and BDNN for solving the high dimensional multioutput problems existed in practical engineering. Since the multiple output responses corresponded to the same input variables， the efficient one-step sampling was implemented and the initial training dataset was established. BDNN was utilized for initially establishing the surrogate model for high dimensional multioutput problem. Because BDNN might provide the uncertainty estimation for multiple predictive output responses simultaneously， an active sampling strategy was proposed for high dimensional multioutput problem. Then， Monte Carlo sampling（MCS） method and Gaussian mixture model were combined for computing the joint probability density function of multiple output responses. The results show that proposed method may avoid the repeated computing processes for different output responses individually， and make full use of the internal relationship among multiple output responses for implementing active learning. Therefore， the efficiency for solving high-dimensional multioutput problems may be improved to some extent. Finally， several numerical examples were utilized to validate the efficiency of the proposed method.

Key words： active learning； Bayesian deep neural network（BDNN）； high dimensional uncertainty； multioutput problem

收稿日期：20240322

基金項目：國家自然科學基金重點項目（52235005）；河南省高等學校重點科研項目計劃（23A460011）；河南工業大學高層次人才科研啟動基金（2022BS025）；國家自然科學基金（52175224）

0? 引言

由于材料屬性、幾何尺寸以及外載荷等不確定因素的存在，造成結構響應具有不確定性的問題廣泛存在于實際工程中［1］。度量與分析輸入不確定因素對結構響應造成的影響及其規律，對提高結構的安全性及可靠性至關重要。

不確定性傳播分析是可靠性分析中的重要環節［2］，其主要任務就是根據輸入變量的統計特性求解結構響應的統計特性（即結構響應的概率密度函數或累積分布函數）。近年來，可靠性分析領域已經發展出較多方法來解決這一問題，這些方法大致可以分為以下幾類：①直接采樣法，包括蒙特卡羅采樣（Monte Carlo sampling， MCS）法［3］以及重要抽樣法［4］等。這類方法直接根據輸入變量的統計規律進行大批量采樣，并根據結構在這些樣本點上的響應求解其統計特性。直接采樣法的主要優點是只要有足夠多的樣本就可以保證求解結果的精確性。②局部近似法，也稱最可能點法，包括一階可靠性方法［5］以及二階可靠性方法［6］等。這類方法利用低階的泰勒展開在最大可能失效點處逼近真實的功能函數，從而簡化計算并提高求解效率。由于采用了基于梯度的迭代策略，當目標問題的非線性程度較低時，局部近似法能夠快速收斂。③基于代理模型的方法，常用的代理模型包括混沌多項式展開（polynomial chaos expansion， PCE）［7］以及Kriging［8］等。這類方法首先建立功能函數的代理模型，進而通過調用代理模型來求解結構響應，以減少對復雜且耗時的數值仿真模型的調用次數。④數值積分法，主要包括單變量降維法（univariate dimension reduction method， UDRM）［9］以及稀疏網格積分法（sparse grid integration method， SGIM）［10］等。這類方法通過數值積分的方式求解結構響應的統計矩，進而利用最大熵方法求解結構響應的概率密度函數。

基于主動學習與貝葉斯深度神經網絡的高維多輸出不確定性傳播方法——劉竟飛? 姜? 潮? 倪冰雨等

中國機械工程第35卷第5期 2024年5月

盡管在不確定性傳播領域已經發展出了一些較為有效的方法，但大多數方法只針對低維問題較為有效。然而，高維不確定性問題廣泛存在于實際工程中，其不確定傳播分析亟待解決［11-12］。高維不確定性傳播分析的難點主要在于：①對于實際工程問題，往往很難顯式地推導出輸入變量與輸出響應之間的映射關系，即目標問題為“黑箱”［13］，因此，無法直觀判斷各輸入變量之間的相互關系以及目標問題的非線性程度強弱，往往需要通過調用耗時的數值仿真模型［14］來計算其響應。對于高維問題，這種“黑箱”效應更加明顯，由于變量數目眾多，為對結構進行更加精準的模擬，需要在有限元模型或計算機仿真程序中考慮更多細節，從而使模擬過程變得更為復雜，即使是單次調用也非常耗時。②對于高維問題，很難根據少量樣本構建其模型并開展不確定性分析，因此，解決高維問題通常需要更多的樣本量來保證求解結果的穩定性與準確性，將給不確定性傳播分析帶來更為嚴峻的效率問題。③現有低維不確定性傳播方法在求解高維問題時，往往會遇到計算誤差大、求解效率低甚至維數災難等問題，無法直接應用于高維問題的求解，如對于一個200維的問題，若采用3階混沌多項式進行求解，則需要計算1 373 701個（百萬級）正交多項式基，為穩定地求解正交多項式的系數，至少需要2×1 373 701個樣本。④在實際工程中，不確定性傳播問題往往具有多個輸出響應［15］，這增加了不確定性傳播分析的難度。

現有低維不確定性傳播方法在求解高維問題時通常會遇到的具體問題包括：①直接采樣法因其巨大的計算量而無法滿足實際工程需求。②局部近似法除了容易陷入局部最優解外，在求解“黑箱”問題時需利用有限差分法求解梯度并更新迭代方向，該步驟往往需要很大的計算量。③現有代理模型方法在建立較為精確的全局代理模型時，所需樣本數量往往隨著輸入變量的維度增加呈現指數級增長，出現“維數災難”［16］。④數值積分法在求解非線性程度較強的高維問題時存在計算精度和效率問題，UDRM法是基于降維策略進行的，容易引入近似誤差，SGIM法所需樣本量會隨著輸入變量維度及積分階次快速增加。

為求解高維不確定性傳播問題，TRIPATHY等［14］利用活躍子空間技術對輸入變量進行降維，降低了構建Kriging模型（也稱作高斯過程回歸模型）的輸入變量維度。BOUHLEL等［11］利用偏最小二乘法［17］對輸入變量進行坐標變換，并在新的坐標空間中篩選出主變量，從而減少構建Kriging模型的輸入變量個數。ZHOU等［18］將稀疏偏最小二乘法與PCE模型相結合，進而求解高維不確定性傳播問題。LATANIOTIS等［19］利用主成分分析對輸入變量進行降維，并結合Kriging模型求解高維不確定性傳播問題。LI等［20］首先利用UDRM構建初步的全局代理模型，然后將Kriging模型與主動學習相結合，對代理模型進行細化。然而，上述方法存在一些缺點：①它們都是基于降維方法開展的，而降維方法本身有其適用條件，如偏最小二乘法適用于輸入變量之間具有較強相關性的問題，而活躍子空間技術則假設僅有少數輸入變量對結構響應的影響較大。對于不滿足這些條件的問題，上述方法可能產生較大誤差。②上述方法僅針對具有單個輸出響應的高維不確定性問題開展研究，而對具有多個輸出響應的高維不確定性問題則無法有效適用。

近年來，基于主動學習的方法已廣泛應用于結構可靠性分析［21］。作為一種代理模型構建方法，其一般求解步驟為：①利用實驗設計方法生成初始樣本點，并初步構建Kriging模型。②根據Kriging模型對預測輸出響應的不確定性估計構造主動加點函數，并通過優化主動加點函數篩選出對提升代理模型精度貢獻最大的輸入樣本點。③通過實驗或數值仿真分析計算與新增輸入樣本點相對應的結構響應，進而更新訓練樣本集與Kriging模型。④重復執行步驟①～步驟③，直至達到收斂條件，即可得到滿足精度要求的代理模型。雖然主動學習方法能夠通過篩選出關鍵樣本點來提高構建代理模型的效率，但利用Kriging模型處理高維問題時可能會遇到維數災難以及參數求解病態的問題，無法有效地解決高維不確定性傳播問題。

近年來，貝葉斯深度神經網絡（Bayesian deep neural network， BDNN）的發展，使上述問題可以得到較好的解決。首先，作為一種深度學習模型，BDNN能夠有效適用于高維多輸出問題。其次，BDNN利用貝葉斯方法進行模型參數求解［22］，能夠實現自適應地正則化，從而有效避免欠擬合或過擬合現象。此外，BDNN能夠求解多個預測輸出響應的不確定性估計［23］，便于通過主動學習［24］的方式構建高維問題的代理模型，從而提升高維不確定性傳播分析的效率。主動學習與BDNN分別具有各自的優點，使其成為解決高維多輸出不確定性傳播問題的重要選擇。

因此，本文提出一種基于主動學習與貝葉斯深度神經網絡的高維多輸出不確定性傳播方法。一方面，該方法能夠有效利用主動學習篩選出對提高代理模型精度貢獻較大的樣本點，從而實現高維多輸出代理模型的快速構建；另一方面，該方法不需要借助降維分析，能夠直接在高維空間中求解多輸出不確定性傳播問題。最后，通過幾個數值算例驗證了所提方法的有效性。

1? 問題描述

首先，對于具有T個輸出響應的結構，其不確定性傳播問題可以表達為［14］

fy（y）=∫Ωδ（y－g（x））fx（x）dx（1）

式中，fy（y）表示T個輸出響應y=（y1，y2，…，yT）的聯合概率密度函數，yT為第T個輸出響應；δ（·）表示Diracs δ函數；g（·）表示多輸出問題模型；fx（x）表示M維輸入變量x=（x1，x2，…，xM）的聯合概率密度函數，xM為第M個輸入變量；Ω為輸入變量的定義域。

對于高維多輸出問題，現有方法大多采用“逐個擊破”的策略，分別針對多個輸出響應進行單獨求解。這樣的方法主要存在以下弊端：①需要反復執行建模與求解過程，不僅使求解變得復雜，甚至會使計算量成倍增加。如采用UDRM或PCE進行高維多輸出不確定性傳播分析時需要分別構建多個代理模型，從而會增加求解復雜程度；再如，當采用Kriging模型及主動學習方法分別求解多個輸出響應時，由于多個主動加點過程中所篩選的樣本點并不完全一致，從而會導致計算量的增加。②單獨求解多個輸出響應時無法利用各輸出響應的內在關聯提高求解效率，進而會造成樣本信息利用不充分。綜上可知，現有方法不能有效地適用于高維多輸出不確定性傳播問題的求解。

2? 本文所提方法

為解決高維多輸出不確定性傳播問題，本文提出一種基于主動學習與貝葉斯深度神經網絡（BDNN）的高維多輸出不確定性傳播方法，所提方法的求解流程如圖1所示。

2.1? 多輸出貝葉斯深度神經網絡

本文所提方法采用BDNN直接構建高維多輸出不確定性問題的代理模型。具有L個隱含層以及T個輸出響應的BDNN如圖2所示，可將其表達為［25］

h（x;τ，θμ）=

ht，L+1（∑HLi=1w（L+1）τ，ihL·

（∑HL－1j=1w（L）i，jhL－1（…）+

b（L）i）+b（L+1）τ）（2）

式中，h（x;τ，θμ）表示BDNN的第τ（τ=1，2，…，T）個輸出響應；hτ，L+1（·）表示BDNN輸出層（即BDNN的第L+1層）中第τ個神經元的激活函數；b（L+1）τ為輸出層中第τ個神經元的偏置參數；θμ為BDNN的模型均值參數向量，θμ=（w（L+1）τ，i，w（m）i，j，b（L+1）τ，b（m）i），其中w（L+1）τ，i為輸出層中第τ個神經元對第L個隱含層中第i個神經元的權重，w（m）i，j（i=1，2，…，Hm；j=1，2，…Hm－1；m=1，2，…，L）為第m個隱含層中第i個神經元對第m-1個隱含層中第j個神經元的權重（Hm為第m個隱含層中的神經元數量），b（L+1）τ為輸出層中第τ個神經元的偏置，b（m）i為第m個隱含層中第i個神經元的偏置；hL（·）表示第L個隱含層中的激活函數；HL 為第L個隱含層中的神經元數量；w（L）i，j（i=1，2，…，HL;j=1，2，…，HL－1）為第L個隱含層中第i個神經元對第L-1個隱含層中第j個神經元的權重。

deep neural network

本文采用貝葉斯方法求解BDNN參數的后驗分布［22］。假設BDNN的各個輸出響應均存在高斯噪聲ε～Ν（0，θσ2），θσ2為高斯噪聲的方差參數，則該輸出響應可以記作g^t（x）=h（x，τ;θμ）+ε，進而可以將BDNN的概率模型表示為

p（g^t（x）|x，θ）=Ν（h（x，τ;θμ），θσ2）（3）

依據貝葉斯原理，BDNN模型參數θ=（θμ，θσ2）與現有訓練樣本集D的聯合概率分布可以表達為BDNN模型參數的先驗分布與其在現有訓練樣本上的似然乘積，即［25］

p（D，θ）=p（θ）p（D|θ）=

p（θμ）p（θσ2）∏Tτ=1∏Dτi=1N（y（i）τ|h（x（i），τ;θμ），θσ2）（4）

D={{（x（1），y（1）1），（x（2），y（2）1），…，（x（N1），y（N1）1）}，

{（x（1），y（1）2），（x（2），y（2）2），…，（x（N2），y（N2）2）}，…，

{（x（1），y（1）T），（x（2），y（2）T），…，（x（NT），y（NT）T）}}

式中，p（θμ）表示BDNN參數均值的先驗分布；p（θσ2）表示BDNN預測輸出響應的方差的先驗分布；Dτ為與第τ個輸出響應對應的訓練樣本數量；y（i）τ為第τ個輸出響應的第i個樣本；（x（NT），y（NT）T）表示與第T個輸出響應對應的第NT個訓練樣本。

在求解得到BDNN參數第i個樣本的后驗分布θ（i）～p（θ|D）后，即可對BDNN模型的參數進行隨機采樣，進而得到BDNN多個預測輸出響應的概率分布［25］：

P（g^τ（x）|x，D）=

∫θp（g^τ（x）|x，θ）p（θ|D）dθ≈

1M′∑M′i=1p（g^τ（x）|x，θ（i））（5）

式中，M′為從BDNN模型參數的后驗分布中進行隨機采樣的樣本數量。

由式（5）可知，BDNN在任意給定輸入變量x*處的預測均值及預測方差可分別表達為

μ（g^τ（x）|D）=1M′∑M′i=1h（x，τ;θ（i）μ）（6）

σ2（g^τ（x）|D）=

1M′∑M′i=1（h（x，τ;θ（i）μ）－

μ（g^τ（x）|D））2+θ（i）σ2（7）

由式（6）和式（7）可知，BDNN能夠同時求解多個預測輸出響應的不確定性估計（即均值和方差），因此，可以利用該特點開展主動學習，篩選出對提高代理模型全局精度貢獻較大的關鍵樣本點，從而提升高維多輸出不確定性傳播問題的求解效率。

2.2? 針對多輸出問題的主動加點方法

如前文所述，研究不確定性傳播是為了求解結構響應的統計特性，因此需要構建具有較高精度的全局代理模型。為了利用主動學習實現高維多輸出問題代理模型的快速構建，本文提出一種針對高維多輸出問題的主動加點策略，可將其表達為

σ-（x）=1T∑Tτ=1σ（g^τ（x）|D）（8）

MUCB1（x）=

maxτ=1，2，…，T{μ（g^τ（x）|D）+βmaxτσ（g^τ（x）|D）max（μ（g^τ（x）|D））－min（μ（g^τ（x）|D））}（9）

MUCB2（x）=

minτ=1，2，…，T{μ（g^τ（x）|D）+βminτσ（g^τ（x）|D）max（μ（g^τ（x）|D））－min（μ（g^τ（x）|D））}（10）

式中，σ-（x）為T個輸出響應的預測方差的均值;MUCB1（x）表示從T個預測輸出響應中可能為極大值點的樣本中篩選出具有最大加點函數的樣本點；MUCB2（x）表示從T個預測輸出響應中可能為極小值點的樣本中篩選出具有最小加點函數的樣本點；βmaxτ為搜索第τ個輸出響應極大值時的可調參數；βminτ為搜索第τ個輸出響應極小值時的可調參數。

所提主動加點策略在每一個迭代步中最多選取三個點。首先，通過最大化式（8）可以篩選出平均預測方差最大的點，該點對降低多輸出模型的預測方差貢獻最大，即在模型平均不確定度最大的地方加點；其次，通過最大化式（9）和式（10）可以從多個預測輸出響應中可能為極值點的樣本中篩選出具有最優加點函數的樣本點，由于在極值點處功能函數的非線性程度通常較高，因此，極值點對提高模型全局精度較為重要。同時，為消除各個輸出響應之間由于尺度效應對主動加點過程造成的影響，在式（9）和式（10）的分母中增加了歸一化項。由于高維代理模型在相鄰迭代步中的更新速度較慢，其極值點更新也較慢，因此，對于式（9）和式（10）中所對應的加點函數，設置為每Δ個迭代步執行一次加點搜索過程，本文取Δ=10。

為判斷所構建的BDNN代理模型是否達到收斂條件，本文采用BDNN在測試數據集上的泛化誤差作為指標，當泛化誤差小于給定閾值ζ時，判定代理模型達到收斂條件。該收斂條件可表示為

L（Dtest;A（Dtrain））<ζ（11）

式中，L（·）表示模型在測試集上的泛化誤差；Dtest為測試數據集；Dtrain為訓練數據集；A（·）表示BDNN模型。

本文所提方法的建模過程可以概括為以下5個步驟：

（1）利用實驗設計方法獲取N0 個初始訓練樣本D（0）={（x（1），y（1）），（x（2），y（2）），…，（x（N0），y（N0））}。同時，利用蒙特卡羅采樣（MCS）方法對輸入變量進行采樣，得到NMCS 個蒙特卡羅樣本X（0）MCS={x（1），x（2），…，x（NMCS）}。

（3）在X（0）MCS中選擇平均方差最大值所對應的輸入樣本作為新增樣本（x，y）。

（4）當迭代步數為10的倍數時，選擇式（9）和式（10）所求解的輸入樣本（即多個預測輸出響應中具有最優加點函數的極大值和極小值點）（x′，y′）和（x″，y″）作為新增樣本。

（5）將新增樣本加入訓練樣本集，并將x*、x′以及x″從X（0）MCS中剔除，得到更新的訓練樣本D（1）以及更新的蒙特卡羅樣本X（1）MCS。循環執行步驟（2）～步驟（4），直至滿足收斂條件。

為了更加清楚地表達所提方法，以具有兩個輸出響應的問題為例，圖3給出了主動加點過程示意圖。對圖3的詳細解釋如下：

（1）如圖3所示，兩個真實功能函數分別為f1（x）=2（x－1）（x－2）sin（3x）+20以及f2（x）=4（x－1）（x－2）sin（3x）。

（2）圖3中紅色虛線和藍色點劃線分別為兩個真實的功能函數曲線，黑色實心點表示現有訓練樣本，紅色和藍色實線分別為由BDNN得到的兩個預測輸出響應。

（3）圖3中藍色和紅色填充區域分別為由BDNN求解的預測輸出響應的兩倍方差區域，綠色點線為當前迭代步中式（8）所對應的平均方差函數曲線，其最大值為紅色五角星所對應的點x*（即新增的樣本點）。

（4）由圖3可以看出，在x*處兩個預測輸出響應的平均不確定性最大，因此，在下一個迭代步中將點x*加入訓練樣本集。與此同時，圖3中紅色三角形和紅色正方形對應的點x′和x″分別為當前迭代步中多個輸出響應的極大值和極小值，在這兩個極值點處，功能函數的非線性程度較高。

2.3? 多輸出響應的概率密度求解方法

通過主動學習構建高維多輸出問題的代理模型后，即可進行不確定性傳播分析。根據式（6）求解出與X（0）MCS={x（1），x（2），…，x（NMCS）}對應的多個輸出響應的統計樣本Y={{μ（g^1（x（1））D），

μ（g^2（x（1））|D），…，μ（g^T（x（1））|D）}，

{μ（g^1（x（2））D），

μ（g^2（x（2））|D），…，μ（g^T（x（2））|D）}，

…，{μ（g^1（x（NMCS））|D），μ（g^2（x（NMCS））|D），…，μ（g^T（x（NMCS））|D）}}，根據這些統計樣本可求解得到多個輸出響應的聯合概率密度函數。

本文采用多變量高斯混合模型求解多個輸出響應的聯合概率密度函數。多變量高斯混合模型可以表達為

fy（y）≈p（y）=∑Kk=1πkN（y|μk，Σk）

∑Kk=1πk=1? 0≤πk≤1（12）

式中，p（y）表示由k（k=1，2，…，K）個高斯分布N（y|μk，Σk）所構成的高斯混合模型（即多輸出響應的聯合概率密度函數）；μk為高斯混合模型的均值向量，μk=（μ1，k，μ2，k，…，μT，k），μT，k為第T個輸出響應的第k個高斯組分的均值；Σk（維度為T×T）為高斯混合模型第k個組分的協方差矩陣;πk為第k個高斯組分的權重系數。

3? 數值算例分析

在本節中，通過兩個輸入變量維度分別為100和200的高維顯式函數以及一個汽車車架受力分析有限元模型算例來驗證所提方法的有效性。將所提方法與主成分分析（principal component analysis， PCA）加高斯過程（Gaussian process， GP）回歸模型方法（以下簡稱PCA-GP方法）、主成分分析加多輸出高斯過程（multioutput Gaussian process， MGP）回歸模型方法（以下簡稱PCA-MGP方法）以及蒙特卡羅采樣（MCS）方法進行對比。其中，PCA-GP方法首先利用PCA 將輸入變量進行降維，然后采用GP回歸模型分別對多個輸出響應進行單獨建模，而PCA-MGP方法首先采用PCA 將輸入變量進行降維，進而采用MGP回歸模型對多個輸出響應進行整體建模。在各算例中，主成分的個數均設置為20，GP回歸模型均采用二次指數核函數，核函數中的超參數通過最大似然估計進行求解。

3.1? 100維顯式函數算例

具有100維輸入變量的顯式函數可表示為

y1=∑100i=1xi+20x21x22+∑99i=2x2ix2i+1－

∑100i=1sin（xi）exp（xi－2）－10

y2=∑100i=1xi+20x21x22+∑99i=2x2ix2i+1－

∑100i=1sin（xi）exp（xi－2）－20

y2=y1－10（13）

在本算例中，令第一個輸入變量服從多峰概率分布x1～（0.5N（1，0.399）+0.5N（1.5，0.449）），其余99個輸入變量均服從正態分布x2～100～N（1，0.1）且各變量之間相互獨立。BDNN的參數設置為：①隱含層數為3；②每個隱含層的神經元數量為100；③采用tanh（·）作為激活函數；④初始訓練樣本數量為1000，主動加點最大迭代步數為1000；⑤MCS方法的采樣個數為106。

各類方法所求解的兩個輸出響應的概率密度函數曲線見圖4和圖5，所求解的兩個輸出響應的前2階中心矩如表1所示。從圖4和圖5中可以看出，所提方法求解得到的概率密度函數曲線可以較好地與MCS所求結果相匹配，且所提方法求解的概率密度函數曲線的整體偏差比采用PCA-GP和PCA-MGP方法時更小。由表1可知，對于所有輸出響應，所提方法求解的第1階中心矩與MCS的求解結果的相對誤差均小于0.2%，所提方法求解的第2階中心矩與MCS的求解結果的相對誤差均小于4%，且所提方法求解結果與MCS求解結果的相對誤差均小于采用PCA-GP和PCA-MGP方法時的相對誤差，表明所提方法在本算例中的表現更為優異，驗證了所提方法的有效性。綜上，算例1結果表明：①BDNN能夠對高維多輸出問題進行有效建模；②所提方法能夠有效求解高維多輸出不確定性傳播問題。

3.2? 200維顯式函數算例

具有200維輸入變量的顯式函數為

在本算例中，令第一個輸入變量服從多峰概率分布x1～（0.5N（1，0.2）+0.5N（1.5，0.15）），其余各輸入變量均服從正態分布x2～200～N（1，0.2）且各變量之間相互獨立。本算例中所提方法的參數設置為：初始訓練樣本數量為1500，主動加點最大迭代步數為500，其他參數與算例1保持一致。

各類方法所求解的兩個輸出響應的概率密度函數曲線見圖6及圖7，所求解的兩個輸出響應的前2階中心矩如表2所示。從圖6和圖7中可以看出，所提方法求解得到的概率密度函數曲線可以較好地與MCS所求結果相匹配，且概率密度函數曲線的整體偏差比采用PCA-GP和 PCA-MGP方法時更小。由表2可知，對于所有輸出響應，所提方法求解的第1階中心矩與MCS的求解結果的相對誤差均小于11%，所提方法求解的第2階中心矩與MCS的求解結果的相對誤差均小于12%，且所提方法求解結果與MCS求解結果的相對誤差均小于采用PCA-GP和PCA-MGP方法時的相對誤差，表明所提方法在本算例中的表現更為優異，驗證了所提方法的有效性。綜上，算例2的結果進一步表明所提方法能夠有效求解高維多輸出不確定性傳播問題。

3.3? 汽車車架受力分析有限元模型算例

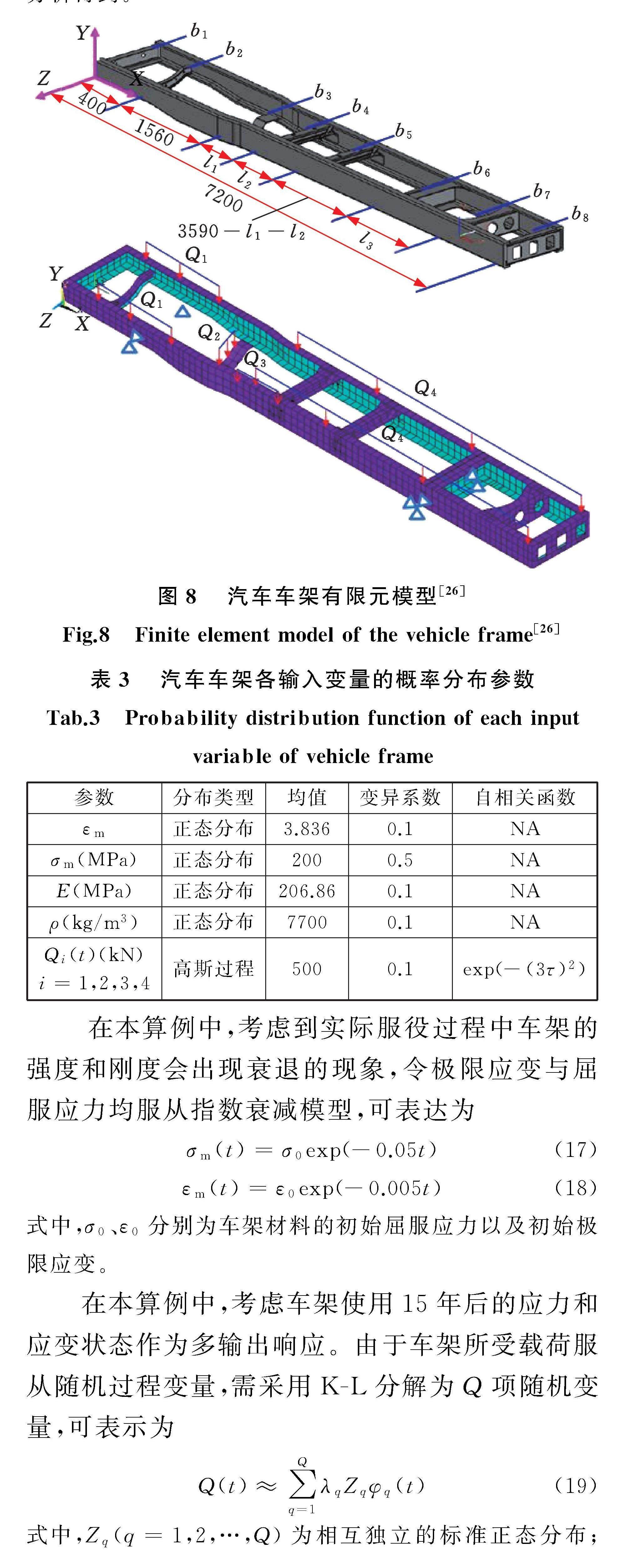
在本算例中，以汽車車架結構的受力分析有限元模型為例來驗證所提方法的有效性。如圖8［26］所示，該汽車車架的結構由8個長度為b1～b8的橫向梁以及2個側向邊梁所構成，該車架總長為7200 mm，各橫梁之間的間距由l1～l3所決定。該車架在等效靜態模型中受到4個服從高斯隨機過程的外力Q1（t）、Q2（t）、Q3（t）、Q4（t），分別為駕駛室、發動機、油箱以及載運貨物產生的作用在汽車車架上的均布力。本算例中，將車架材料的泊松比設置為0.3，車架材料的密度ρ和彈性模量E設置為隨機變量，各參數的具體信息如表3所示。根據應力與應變失效準則，可以將汽車車架服役過程中的應力與應變功能函數表達為

g1（t）=σm（t）－σmax（ρ，E，Q（t））（15）

g2（t）=εm（t）－εmax（ρ，E，Q（t））（16）

式中，σm（t）、εm（t）分別為不同時刻t下汽車車架的材料屈服應力和材料極限應變；σmax（ρ，E，Q（t））、εmax（ρ，E，Q（t））分別為不同時刻t下的最大真實應力和最大真實應變，應力和應變的確定解可以通過車架的有限元仿真分析得到。

在本算例中，考慮到實際服役過程中車架的強度和剛度會出現衰退的現象，令極限應變與屈服應力均服從指數衰減模型，可表達為

σm（t）=σ0exp（－0.05t）（17）

εm（t）=ε0exp（－0.005t）（18）

式中，σ0、ε0分別為車架材料的初始屈服應力以及初始極限應變。

在本算例中，考慮車架使用15年后的應力和應變狀態作為多輸出響應。由于車架所受載荷服從隨機過程變量，需采用K-L分解為Q項隨機變量，可表示為

Q（t）≈∑Qq=1λqZqφq（t）（19）

式中，Zq（q=1，2，…，Q）為相互獨立的標準正態分布；λq、φq分別為協方差函數的第q個特征值和第q個特征函數。

在該算例中，K-L展開的網格長度設置為0.25，則時間節點共有61個，通過K-L展開的前100項逼近隨機過程變量，則在本算例中一共有104個輸入變量。本算例中所提方法的參數設置為：初始訓練樣本數量為1000，主動加點最大迭代步數為500，其他參數與算例1中保持一致。

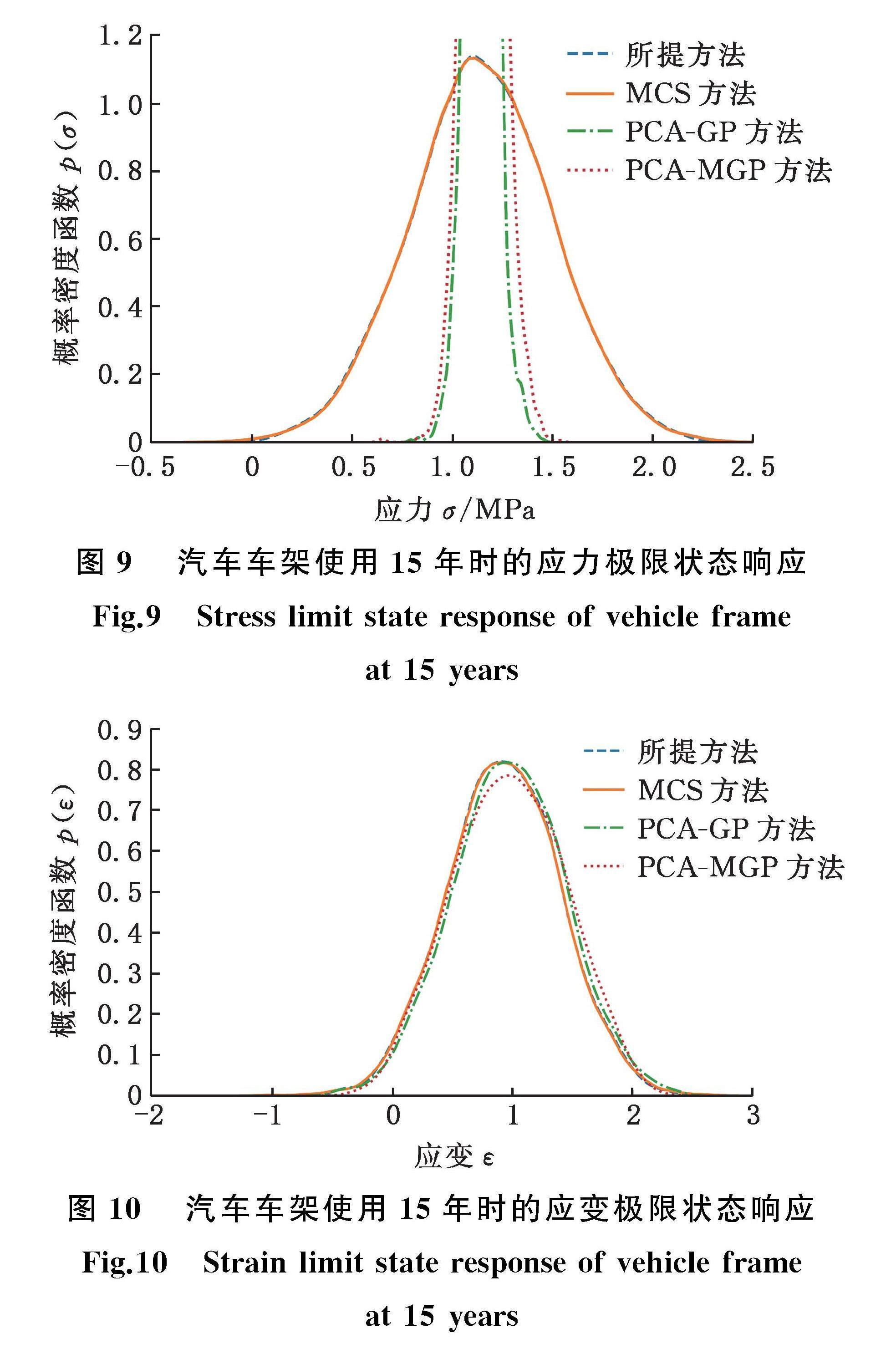
各類方法所求解的兩個輸出響應（即應力σ和應變ε）的概率密度函數曲線見圖9及圖10，所求解的兩個輸出響應的前2階中心矩如表4所示。從圖9和圖10中可以看出，所提方法求解得到的概率密度函數曲線可以較好地與MCS所求結果相匹配，且概率密度函數曲線的整體偏差比采用PCA-GP和PCA-MGP方法時更小。由表4可知，對于所有輸出響應，所提方法求解的第1階中心矩與MCS的求解結果的相對誤差均小于0.1%，所提方法求解的第2階中心矩與MCS的求解結果的相對誤差均小于2%，且所提方法求解結果與MCS求解結果的相對誤差均小于采用PCA-GP和PCA-MGP方法時的相對誤差，表明所提方法在本算例中的表現更為優異，驗證了所提方法的有效性。綜上，算例3的結果再次表明所提方法能夠有效求解高維多輸出不確定性傳播問題。

4? 結論

本文將主動學習與貝葉斯深度神經網絡相結合，充分利用二者的特點和優勢，提出一種針對高維多輸出問題的不確定性傳播方法。所提方法具有以下優勢：

（1）能夠在不引入降維誤差的前提下，直接在高維空間中構建多輸出問題的代理模型。

（2）利用貝葉斯深度神經網絡以及多個輸出響應的內在關聯開展主動學習，有效避免了分別對多個輸出響應進行單獨求解的復雜過程以及由此造成的計算量增加問題。三個數值算例的分析結果表明，所提方法能夠有效求解高維多輸出不確定性傳播問題。

本文嘗試提出一種新的解決方案來求解高維多輸出不確定性傳播問題。所提方法與現有單輸出高維不確定性傳播方法的主要區別包括：

（1）所提方法能夠直接在高維空間中實現多輸出問題模型的一次性構建，而現有單輸出高維不確定性傳播方法需要分別針對多個響應單獨求解，因此，所提方法可以降低求解過程的復雜程度。

（2）所提方法通過主動學習的方式進行建模，能夠利用多個輸出響應之間的內在關聯開展主動學習，且在主動學習的每一個迭代步中，僅對多輸出模型影響較大的輸出響應進行加點，并不是對所有輸出響應都新增相同數量的樣本點，因此，所提方法可以在一定程度上提高多輸出問題的求解效率。而對于現有單輸出高維不確定傳播方法，一方面，它們大都基于降維分析進行建模，容易在降維環節引入誤差；另一方面，在針對多輸出問題進行單獨建模時，各個模型所需的樣本點不能共享，可能導致計算量增加。

（3）根據算例分析結果，所提方法能夠較好地求解出多個輸出響應的概率密度函數曲線，且在相同樣本點數量的前提下，所提方法求解出的前兩階中心矩與蒙特卡羅采樣方法求解結果的相對誤差小于采用其他算法時的相對誤差，驗證了所提方法的有效性。

在后續研究中仍需進一步改進和發展的方向包括：

①所提方法針對多個輸出響應對應同一組輸入變量的問題較為有效，對各個輸出響應分別對應不同輸入變量的情況考慮不夠全面；

②如何將所提方法擴展至高維可靠性分析與優化設計中［27-28］，并提升高維可靠性問題的求解效率，是一個值得繼續研究的方向。

參考文獻：

［1］? YANG Meide， ZHANG Dequan， HAN Xu. New Efficient and Robust Method for Structural Reliabi-lity Analysis and Its Application in Reliability-based Design Optimization［J］. Computer Methods in Applied Mechanics and Engineering， 2020， 366：113018.

［2］? LIU Jingfei， JIANG Chao， ZHENG Jing. Uncertainty Propagation Method for High-dimensional Black-box Problems via Bayesian Deep Neural Network［J］. Structural and Multidisciplinary Optimization， 2022， 65：83.

［3］? ROBERT C， CASELLA G. Monte Carlo Statistical Methods［M］. New York：Springer Science & Business Media， 2013.

［4］? MORI Y， KATO T. Multinormal Integrals by Importance Sampling for Series System Reliability［J］. Structural Safety， 2003，25：363-378.

［5］? RACKWITZ R， FLESSLER B. Structural Reliabi-lity under Combined Random Load Sequences［J］. Computers & Structures， 1978， 9：489-494.

［6］? ZHANG Jun， DU Xiaoping. A Second-order Reli-ability Method with First-order Efficiency［J］. Journal of Mechanical Design， 2010， 132：101006.

［7］? BLATMAN G， SUDRET B. Adaptive Sparse Polynomial Chaos Expansion Based on Least Angle Regression［J］. Journal of Computational Physics， 2011， 230：2345-2367.

［8］? YANG Meide， ZHANG Dequan， WANG Fang，et al. Efficient Local Adaptive Kriging Approximation Method with Single-loop Strategy for Reliability-based Design Optimization［J］. Computer Methods in Applied Mechanics and Engineering， 2022， 390：114462.

［9］? RAHMAN S， XU H. A Univariate Dimension-reduction Method for Multi-dimensional Integration in Stochastic Mechanics［J］. Probabilistic Engineering Mechanics， 2004， 19：393-408.

［10］? XIONG F F， GREENE S， CHEN W， et al. A New Sparse Grid Based Method for Uncertainty Propagation［J］. Structural and Multidisciplinary Optimization， 2010， 41：335-349.

［11］? BOUHLEL M A， BARTOLI N， OTSMANE A， et al. Improving Kriging Surrogates of High-dimensional Design Models by Partial Least Squares Dimension Reduction［J］. Structural and Multidisciplinary Optimization， 2016， 53：935-952.

［12］? SCARTH C， SARTOR P N， COOPER J E， et al. Robust and Reliability-based Aeroelastic Design of Composite Plate Wings［J］. AIAA Journal， 2017， 55（10）：3539-3552.

［13］? 高進，崔海冰，樊濤，等.一種基于自適應Kriging集成模型的結構可靠性分析方法［J］.中國機械工程， 2024， 35（1）：83-92.

GAO Jin， CUI Haibing， FAN Tao， et al. A Structural Reliability Analysis Method Based on Adaptive Kriging Ensemble Model［J］. China Mechanical Engineering， 2024， 35（1）：83-92.

［14］? TRIPATHY R， BILIONIS I， GONZALEZ M. Gaussian Processes with Built-in Dimensionality Reduction：Applications to High-dimensional Uncertainty Propagation［J］. Journal of Computational Physics， 2016， 321：191-223.

［15］? 趙錄峰，呂震宙，王璐. 隨機-區間混合不確定性多輸出模型確認指標［J］.哈爾濱工業大學學報， 2018， 50（4）：78-84.

ZHAO Lufeng， LU Zhenzhou， WANG Lu. Confirmation Metrics for Stochastic Interval Mixed Uncertainty Multi Output Models［J］. Journal of Harbin Institute of Technology， 2018， 50（4）：78-84.

［16］? LUTHEN N， SUDRET B. Adaptive Sparse Polynomial Chaos Expansions：a Survey［C］∥GAMM Annual Meeting. Vienna， 2019：000336501.

［17］? PEREZ R A， GONZALEZ F G. Partial Least Squares Regression on Symmetric Positive-definite Matrices［J］. Revista Colombiana de Estadística， 2013， 36：177-192.

［18］? ZHOU Yicheng， LU Zhenzhou， HU Jie， et al. Surrogate Modeling of High-dimensional Problems via Data-driven Polynomial Chaos Expansions and Sparse Partial Least Square［J］. Computer Methods in Applied Mechanics and Engineering， 2020， 364：112906.

［19］? LATANIOTIS C， MARELLI S， SUDRET B. Extending Classical Surrogate Modelling to Ultrahigh Dimensional Problems through Supervised Dimensionality Reduction：a Data-driven Approach［J］. ArXiv：Machine Learning， 2018， arXiv：1812.06309.

［20］? LI M， SADOUGHI M， HU Z， et al. Reliability-based Design Optimization of High-dimensional Engineered Systems Involving Computationally Expensive Simulations［C］∥AIAA Non-deterministic Approaches Conference. Kissimmee， 2018：2171.

［21］? ZHAN Hongyou， XIAO Ningcong， JI Yuxiang. An Adaptive Parallel Learning Dependent Kriging Model for Small Failure Probability Problems［J］. Reliability Engineering & System Safety， 2022， 222：108403.

［22］? NEAL R M. Bayesian Learning for Neural Networks［M］. New York：Springer Science & Business Media， 2012.

［23］? LEE J， BAHRI Y， NOVAK R， et al. Deep Neural Networks as Gaussian Processes［J］. ArXiv Preprint， 2017， arXiv：1711.00165.

［24］? GAL Y， ISLAM R， GHAHRAMANI Z. Deep Bayesian Active Learning with Image Data［C］∥Proceedings of the 34th International Conference on Machine Learning. Sydney， 2017：1183-1192.

［25］? SPRINGENBERG J T， KLEIN A， FALKNER S， et al. Bayesian Optimization with Robust Bayesian Neural Networks［C］∥Advances in Neural Information Processing Systems. Barcelona， 2016：4134-4142.

［26］? JIANG Chao， HAN Xu， LI Wenxue， et al. A Hybrid Reliability Approach Based on Probability and Interval for Uncertain Structures［J］. Journal of Mechanical Design， 2012， 134（3）：31001.

［27］? YANG Meide， ZHANG Dequan， JIANG Chao， et al. A New Solution Framework for Time-dependent Reliability-based Design Optimization［J］. Computer Methods in Applied Mechanics and Engineering， 2024， 418：116475.

［28］? YANG Meide， ZHANG Dequan， JIANG Chao， et al. New Efficient and Robust Method for Structural Reliability Analysis and Its Application in Reliability-based Design Optimization［J］. Reliability Engineering & System Safety， 2021，215：107736.

（編輯? 胡佳慧）

作者簡介：

劉竟飛，男，1991年生，講師、博士。研究方向為基于深度學習的復雜裝備不確定性建模與可靠性設計。E-mail：liujingfei@haut.edu.cn。

姜? 潮（通信作者），男，1978年生，教授、博士研究生導師。研究方向為復雜裝備先進可靠性設計技術、高端特種機器人技術以及先進車身設計制造。E-mail：jiangc@hnu.edu.cn。