發展科學思維的高中物理模型建構教學策略

摘 要：在高中物理教學中，建構物理模型是解決物理問題的重要科學思維方式。這一過程包括創造與生活緊密相關的真實情境、將生活情境轉化為物理情境、物理模型的建構以及模型的應用。通過實施這些策略，教師不僅能有效地發展學生的科學思維能力，同時也能顯著提升學生的學習效果。

關鍵詞：科學思維；模型建構；情境

1 科學思維與模型建構的內涵

1.1 科學思維的內涵

科學思維是一種獨特的思考方式，指運用科學方法來細致觀察自然現象，通過嚴謹實驗、深入推理和準確判斷等方法來揭示事物的本質和規律。在這個過程中，科學家進行科學研究的基本方法包括觀察、實驗、歸納、演繹、類比、假設、驗證等環節。在物理學科核心素養中，科學思維是一種獨特且重要的認識方式，它從物理學的專業視角出發，對客觀事物的本質屬性、內在規律以及事物間的相互關系進行深入的認識和理解。這個過程是通過分析綜合、推理論證等方法，基于經驗事實建構物理模型的抽象概括過程，也是科學領域中具體運用這些方法的體現。此外，科學思維強調在事實證據的基礎上，通過科學推理對各種觀點和結論進行嚴格的質疑和批判，并進行檢驗和修正。這種思維方式能夠激發學生創造性的見解，進一步提升學生的認知能力。在教學過程中，教師應當積極引導學生以科學的視角觀察問題，按照科學的邏輯思考問題，并采取具體且有效的方法來解決問題。

1.2 模型建構的內涵

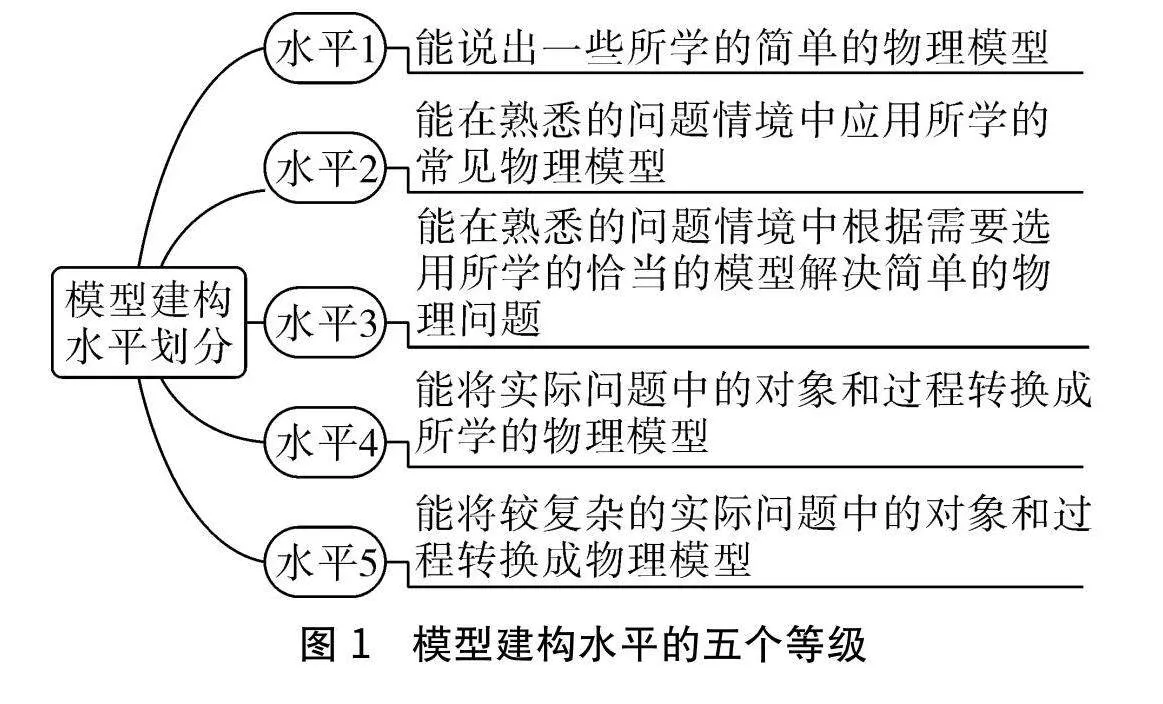
模型建構是指基于經驗事實通過抽象、概括和簡化，將現實生活中的復雜現象和問題轉化為易于理解的模型，以便進行深入研究和探討。建構物理模型是解決物理問題的一種科學思維方式，它有助于深入揭示事物的本質規律。在建構物理模型的過程中，我們需要將外部條件中可能對研究對象產生干擾的次要因素排除在外，以突出其本質特征或最主要方面。此外，我們還可以通過將物理過程純粹化、理想化來建構物理模型。《普通高中物理課程標準（2017年版2020年修訂）》（以下簡稱《課程標準》）中對模型建構水平劃分了五個等級

（見圖1）^［1］，這為教師評估學生在模型建構方面的能力和水平提供了依據。

2 高中物理教學中模型建構的必要性

2.1 《中國高考評價體系說明》和《課程標準》的要求

《中國高考評價體系說明》要求高考要圍繞學科主干內容，加強對基本概念、基本思想方法的考查。通過設置真實的問題情境，考查學生靈活運用所學知識分析解決問題的能力，使學生擺脫“死記硬背”“機械刷題”“題海戰術”，引導學生從“解題”向“解決問題”轉變。^［2］《課程標準》在教學建議中指出，發展學生的科學思維能力是重要的教學目標之一，建構模型是一種重要的科學思維方法。^［3］隨著學生思維的發展，他們自然會從“題海戰術”的“解題”過程中走出來，能夠運用所學知識解決實際問題。

2.2 高中物理教學的迫切需要

高中物理涉及力學、電磁學、光學、熱學等多個領域，知識體系龐大復雜，需要學生具備較強的綜合分析能力。而將理論知識應用于實際問題的解決，還需要學生具備較強的實踐能力和應用能力。由于高三教學基本都是復習課的形式，教學內容屬于舊知識，很多復習課成了知識點羅列式的簡單重復；學生對于所學知識的遷移能力不夠高，面對試題中復雜的情境往往感到困惑，無法準確識別熟悉的知識點，也就是說，他們未能將實際情境與物理知識進行有效的關聯。為了培養學生的物理分析能力，教師需要引導他們參與物理模型的建構過程，并幫助他們掌握模型建構的思維方法。這樣才能幫助學生更好地運用物理知識解決問題。

3 發展科學思維的高中物理模型建構教學路徑

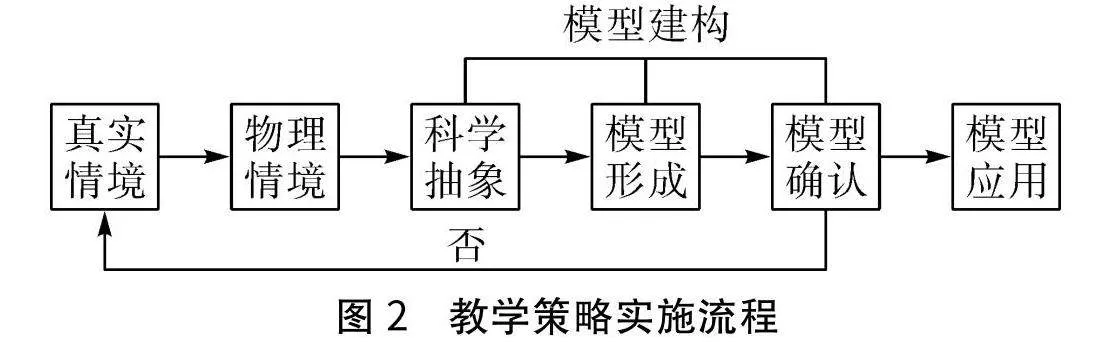
科學思維不像物理知識那樣可以直接讀取獲得，科學思維的培養需要大腦按照一定的方法對知識進行加工。模型建構是非常重要的方法，包含分析、抽象、概括、推理以及論證等思維方法。在高中物理教學中，如何利用模型建構來提高學生的科學思維能力是一個重要的問題。筆者在教學實踐中，摸索出以下教學策略，其實施流程如圖2所示。該教學策略旨在發展學生的科學思維以提高學習效率。

3.1 創設貼近生活的真實情境

教師在設計教學內容時，應努力創設與現實生活緊密相關的真實情境，有效激發學生的學習興趣。在復習動量守恒定律及其應用時，碰撞模型是常被探討的一個重點。在這一教學環節中，教師可以巧妙地建構一個生動的真實情境：首先，演示一小彈性球自由下落并與地面碰撞后反彈的過程；隨后，將小彈性球疊放在較大的彈性球上，從相同高度一同釋放，觀察兩者的碰撞及反彈情況。

演示結束后，教師可適時拋出引人深思的問題：“為什么當小球疊放在大球上，兩者一同撞擊地面后，小球的反彈高度會比單獨下落時更高呢？”此問題旨在激發學生的好奇心，點燃他們探索物理奧秘的熱情。

3.2 生活情境轉化為物理情境

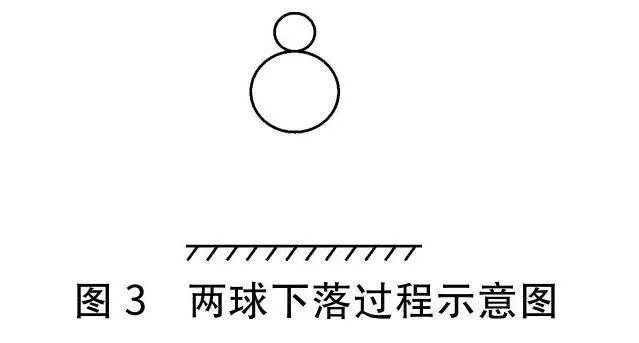
在建構物理模型的過程中，我們需要將真實的生活情境轉化為解決物理問題的具體情境。教師可以播放提前錄好的慢鏡頭下兩個疊放球下落的視頻，幫助學生形成直觀的視覺印象。隨后，教師引導學生畫出兩球下落過程的示意圖（見圖3）。通過這個過程，學生會發現大球與地面碰撞反彈后，兩球也發生了碰撞。這使他們能夠聯想高中物理中的碰撞問題，從而順利地將問題中的實際情境轉化為兩球碰撞的情境。

3.3 物理模型建構

在物理學習中，模型建構是一種重要的方法，學生可以通過觀察和分析問題情境，運用所學的知識來建構物理模型。建構物理模型的步驟通常包括三個階段：一是科學抽象階段，將問題簡化為基本的物理要素；二是模型形成階段，根據物理規律和理論建構物理模型；三是模型確認階段，通過實驗驗證和理論分析，確保模型的準確性和可靠性。

在科學抽象階段，學生需要運用思維對物理情境進行深度加工，準確提煉出研究對象的本質特征。他們需要敏銳地識別出情境中的關鍵要素以及這些要素之間的相互關系，同時忽略次要因素，從而將注意力集中于核心問題上。

在模型形成階段，學生需要將頭腦中已有的相關物理模型與物理對象的本質特征進行比對，從而建構出合適的模型。這個過程需要學生對所學知識進行整合和應用，以便將問題與已知的物理模型相匹配。

在模型確認階段，學生需要依據所建構的物理模型，尋找解決問題的相關物理規律和路徑，并嘗試運用這些規律和路徑解決問題。他們需要驗證模型的準確性，并確定它是否能夠有效地解釋和預測現象。如果問題得以順利解決，那么意味著物理模型的建構是成功的；如果問題無法得到解決，學生則需要重新建構物理模型。

在進行情境轉化后，教師可以引導學生思考兩球的碰撞是否滿足高中物理“碰撞”的本質特征這一問題。在水平面上，兩球互相碰撞會有三種情況，一是質量相等的兩球碰撞，二是質量小的球碰撞質量大的球，三是質量大的球碰撞質量小的球，這里屬于第二種情況。學生對這個碰撞模型已經非常熟悉，因此可以在此基礎上進一步確認。由于兩球都是彈性球，我們可以認為兩球發生的是彈性碰撞，即碰撞過程沒有能量損失，碰撞過程內力遠大于球的重力。在嘗試解決問題的過程中，我們需要運用這兩個規律，并驗證模型的準確性。

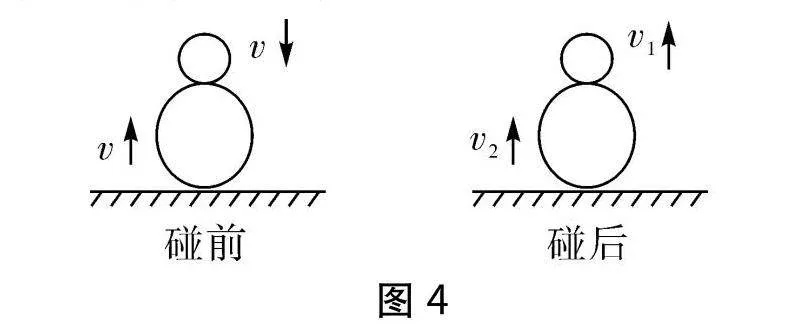
假設兩球的質量分別為m₁、m₂，且m1＜m₂，忽略兩球直徑的影響。在大球落地瞬間，兩球速度大小都為v，大球與地面碰撞后原速率反彈，小球速度大小仍然為v，兩球碰撞后小球與大球的速度大小分別為v1和v2，如圖4所示。

【分析模型】

取向上為正方向，根據動量守恒定律列方程得

m2v－m1v＝m2v2＋m1v1。

根據機械能守恒定律列方程得

12m2v2＋12m1v2＝12m₂v2₂＋12m1v2₁。

聯立以上兩式，解得

v1＝3m2－m1m₁＋m2v。

情況一：若m₂＝m₁，則v₁＝v；

情況二：若m2＝2m₁，則v₁＝53v；

情況三：若m₂＝3m₁，則v₁＝2v；

情況四：若m2＝4m1，則v₁＝115v；

情況五：若m2m1，則v1≈3v。

由以上分析可知，大球與小球的質量相差越大，小球反彈后的速度就越大。小球碰撞后可達到的最大速率是碰撞前速率的3倍，這樣就可以解釋為什么小球疊放在大球上反彈的高度會更高了。

3.4 模型應用

學生利用所建構的物理模型，解決實際問題，提高解決問題的能力。

例題 某興趣小組同學利用一組大小、質量各不相同的硬質彈性小球進行了若干次碰撞實驗。所有碰撞都可認為是彈性碰撞，重力加速度大小為g，忽略空氣阻力影響，小球均可視為質點。試討論以下問題：

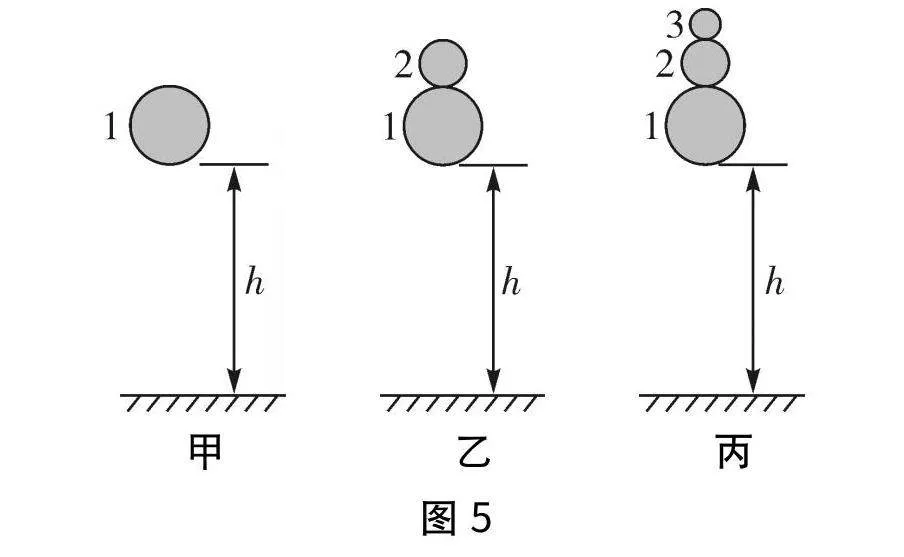
（1）第一次實驗他們將一個質量為m₁的球1從距離地面高h處由靜止釋放，如圖5甲所示。通過查閱資料他們估計出了球與地面的作用時間Δt。求球1與地面碰撞過程中地面對小球的平均作用力F的大小。

（2）第二次實驗在球1頂上放一質量為m2的球2，m₁＞m₂，讓這兩個球一起從距離地面高h處自由下落并撞擊地面，如圖5乙所示，他們驚奇地發現球2反彈的高度超過了釋放時的高度。他們猜想若球2質量越小，則被反彈的高度越高。試從理論角度分析他們的猜想是否正確，并求球2能達到的最大高度。

（3）受第（2）問的啟示，他們設想了一個超球實驗：將三個球緊貼從距離地面高h處由靜止釋放，由下至上三球的質量分別為m₁、m₂和m₃，且滿足m₁m₂m₃，如圖5丙所示。他們設想球3可以被反彈到很高的高度，請你幫他們試估算此高度。

【第（1）問的解析】

球1做自由落體運動，根據

v2＝2gh，

可得落地瞬間速度大小為

v＝2gh。

由于是彈性碰撞，所以反彈速度大小為

v＝2gh。

設向下為正方向，從落地到反彈，根據動量定理可得

（mg－F）Δt＝－mv－mv，

解得

F＝mg＋2mvΔt＝mg＋2m2ghΔt。

【第（2）問的解析】

球1以碰前剛剛著地的速率反彈并與球2碰撞，設向上為正方向，設碰后小球1速度為v₁，球2碰后速度為v₂，根據動量守恒定律可得

m1v－m2v＝m2v2＋m1v1，

根據機械能守恒定律可得

12m2v2＋12m1v2＝12m2v²₂＋12m1v2₁，

聯立解得

v1＝m₁－3m₂m₁＋m₂2gh；

v2＝3m1－m₂m₁＋m₂2gh。

對于球2碰后根據動能定理可得

－m₂gh₁＝0－12m₂v²₂，

解得

h1＝3m1－m₂m₁＋m₂²h＝3－m₂m₁1＋m₂m₁²h。

又因為m₁＞m₂，所以m₂m₁ ＜1 ，則h₁＞h。當m₁m₂時，h₁的值最大，最大值為9h，即球2反彈以后能上升的最大高度是開始下落高度的9倍。

【第（3）問的解析】

在第（2）問的基礎上，球2接著與球3碰撞，因為m₁m₂，

所以v₂＝32gh。

同理根據動量守恒定律以及機械能守恒定律得出球3可以被反彈的高度的表達式

h₂＝

7m₂－m₃m₂＋m₃²h＝

7－m₃

m₂

1＋m₃m₂²h。

又因為m₂m₃，所以h₂的最大值為49h，即球3被反彈的最大高度為49h。

【點評】

學生需要為了回答第（1）問而建構自由落體運動模型和碰撞模型，并熟練運用自由落體運動的規律和動量定理來分析和解決這一問題。第（2）問則要求學生在已經成功建構的這些物理模型基礎上，進行更為深入的分析和探討。在解決第（3）問時，學生應基于第（2）問的深入分析結果，進一步進行推理分析，以期得出最終的答案。

4 結語

教師在教學實踐中要有意識地引導學生參與物理模型的建構過程，從而培養他們掌握模型建構的思維方法。這不僅能提高學生應用物理知識分析解決問題的能力，還有助于他們更好地理解和應對復雜的真實情境。在模型建構的過程中，學生可以更加深入地理解物理概念和規律，并將其應用于解決實際問題，進一步發展科學思維。

參考文獻

［1］［3］中華人民共和國教育部.普通高中物理課程標準（2017年版 2020年修訂）［M］.北京：人民教育出版社，2020：46-48，51.

［2］教育部考試中心.中國高考評價體系說明［M］. 北京：人民教育出版社，2019：18.