小學數(shù)學圖形與變換教學的思考

江國基

摘 要： 小學生在學習抽象的幾何概念時，往往要借助直觀形象的教學過程完成。所以，教師應從實際生活入手，挖掘有效的數(shù)學教學素材資源，創(chuàng)設變換教學情境，以多變換的視角欣賞、分析圖形，幫助學生掌握圖形與變換的基本規(guī)律與概念。

關鍵詞： 小學數(shù)學 圖形與變換 情境教學

“圖形與變換”作為小學數(shù)學新課程“空間與圖形”領域中四個內(nèi)容板塊（圖形的認識、測量、圖形與變換、圖形與位置）之一，由于這部分內(nèi)容較抽象，對于這部分知識的教學，數(shù)學教師往往感到比較難以入手。我認為從以下方面入手可以有效強化這部分內(nèi)容的教學效果。

一、創(chuàng)設教學情境，重視變換過程體驗

教材在編排“圖形與變換”的內(nèi)容時，重視學生在具體情境中直觀認知變換現(xiàn)象，然后通過操作活動體會變換的特征，這實際上也符合學生對于事物的認識過程。其實，學生很早就有了物體或圖形運動的經(jīng)驗，他們通過折紙、轉風車、照鏡子等獲得諸如平移、旋轉、反射等體驗，生活中的許多現(xiàn)象，如旗幟升起、螺旋槳轉動等，以及建筑，植物（如楓葉）、動物（如蝴蝶）等物體為學生認識移、旋轉、反射提供了豐富素材。教師應注意收集并利用這些素材資源，鼓勵學生對這些素材加以分析，從而直觀認識變換現(xiàn)象。教師還應鼓勵學生通過操作活動整體感受變換的特征。

在直觀認識變換現(xiàn)象和整體感受變換的特征的基礎上，學生可以嘗試在方格紙上畫出一個圖形經(jīng)變換后的圖形或者探索圖形經(jīng)過了什么樣的變換。這一要求既是對整體感受變換特征的應用，又是從整體感受變換現(xiàn)象到初步刻畫變換特征的一個過渡。

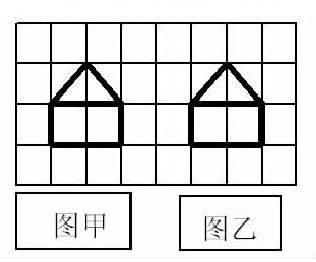
如案例：方格圖中的圖甲向右平移（ ）個格得到圖乙。

學生解決這一問題，不僅要從整體上感受變換現(xiàn)象，而且要開始探索如何刻畫平移。這一內(nèi)容在教材上都一般安排在三年級，實際上三年級的學生在處理這個問題時還是存在一些困難的，比如，學生在找平移格數(shù)時，常常不會找平移前后兩個對應點之間的格數(shù)，而是房子中間空白那一段的格數(shù)，得到平移2格的錯誤答案。此時，教師會運用這樣的策略：鼓勵學生觀察局部的點（如房子頂）的變化情況，通過一格一格地數(shù)而尋找正確的格數(shù)。這已經(jīng)開始從整體感知變換到細致刻畫變換了，當然這個過程是通過操作實現(xiàn)的。教學中需要注意的是，第一，操作應該與適當?shù)南胂笙嘟Y合。低年級可以先操作然后回想變換的過程，到了高年級可以先想象，然后再操作，然后再回想。第二，教師還應明確教學要求，特別是作圖的要求。首先小學階段的作圖是在方格紙上。另外，對于平移的作圖，只要求做基本圖形沿水平方面、豎直方向的平移；對于旋轉來說，要求做基本圖形旋轉90度后的圖形。

二、圖形教學應從變換的視角去學習

從變換的角度認識圖形為學生把握圖形提供了動態(tài)角度，圖形的變換是研究幾何問題的有效工具，引進變換能使圖形動起來，有助于發(fā)現(xiàn)圖形的幾何性質，同時也使學生感受到圖形變換與圖形認識的聯(lián)系。例如在圖形的認識中，對于正方形、長方形、圓等，可以通過折疊等活動認識它們的軸對稱性。對于學有余力的學生，教師還可以從以下三方面進行適當延伸，使學生從動態(tài)的角度更好地認識這些圖形。第一，可以設計適當活動（圓的旋轉對稱性的活動），使學生對圓的旋轉對稱有初步感受，包括平行四邊形，這也會解決學生的一些困惑（如平行四邊形這么“對稱”，為什么一般的平行四邊形不是軸對稱圖形呢？）。第二，可以討論這些圖形對稱軸條數(shù)的不同，從而感受到圓是一個最具“對稱”性的圖形。第三，可以通過軸對稱性探索或驗證圖形的性質。比如，有的學生將正方形沿對邊對折，以及沿對角線對折，從而說明正方形四個角都相等，是直角。

實際上，學生對于圖形的對稱性質是比較感興趣也是容易出現(xiàn)困惑的，特別是對于平行四邊形，如在教學中發(fā)現(xiàn)：盡管教師反復強調(diào)了“對折”后能完全重合的圖形是軸對稱圖形，但實際還有不少學生認為一般的平行四邊形是軸對稱圖形。為什么會這樣呢？一次課后，與一名同學討論了這個問題，學生說：“我承認一般平行四邊形不是軸對稱圖形，但它是那么的對稱，那么規(guī)整，所以就特別想把它兩部分重合，如軒一下就能重合了。”實際上，這位同學關注到了對稱，盡管一般平行四邊形不是軸對稱圖形，但它是中心對稱圖形（圖形沒平行四邊形中心旋轉180度后就和原來的圖形重合了）。盡管中心對稱圖形概念還不是小學階段所要掌握的，但教師可以捕捉學生的思想閃光點，幫助學生通過變換來刻畫之，積累經(jīng)驗，而不是簡單的對錯評價。

三、指導學生從變換的視角觀察和分析生活中的圖案

學習圖形與變換內(nèi)容的一個重要目的是使學生運用數(shù)學的眼光看待現(xiàn)實世界。學生應能在生活中發(fā)現(xiàn)并欣賞變換的應用，并運用變換的知識分析有關的現(xiàn)象。進一步體會數(shù)學對人類社會的作用，體會數(shù)學的文化價值。例如，在生活中隨處可見的美麗圖案，學生在觀察這些圖案時，將發(fā)現(xiàn)其中包含的熟悉的圖形；將運用數(shù)學的眼光分析圖案的組成，等到學習了變換以后，學生就可以從變換角度欣賞圖案，如是否運用了變換，一個基本圖形發(fā)生了怎樣的一個變換之后，形成了這么美妙的一個圖案；將欣賞這些各具特色的圖案，發(fā)現(xiàn)其中蘊涵的對稱美、和諧美、簡明美；將以此為啟發(fā)，發(fā)揮自己的個性和創(chuàng)造力，親自動手設計圖案以靈活運用所學的變換，并從中體會創(chuàng)造的樂趣與艱辛。

運用變換進行圖案設計是一個好的實踐活動，學生將在這一活動中進一步理解變換的性質，體會變換的應用價值，并充分發(fā)揮自己的個性和創(chuàng)造力，領略圖形世界的神奇。為了打開學生思路，可以先讓他們觀察現(xiàn)實生活中由變換形成的圖案，并以此為啟發(fā)設計自己的圖案。

綜上所述，圖形與變換的學習既不同于對變換幾何的形式化研究，又不是簡單的變換現(xiàn)象欣賞。在這部分內(nèi)容的教學中，應引導學生觀察現(xiàn)實生活中的現(xiàn)象并通過操作、推理、想象等自覺地加以數(shù)學上的分析，進一步豐富數(shù)學活動經(jīng)驗和體驗，促進他們觀察、分析、歸納、概括等一般能力和積極的情感態(tài)度、審美意識等的發(fā)展。