高中數學教學中運用數形結合提高解題能力的探索

鄒衛剛

摘 要：本文首先對數形結合進行了概述，然后分析了數形結合的“化形為數、化數為形”及“數形兼顧”的三種類型，然后從培養學生運用數形結合思想解決數學問題的意識、更新教學觀念，轉變學習方式及重視分析數形結合思想解題出現的錯誤三個方面詳細論述了高中數學教學中運用數形結合思想的策略。

關鍵詞：高中 數學 數形結合 解題能力 策略

中圖分類號：G633.6 文獻標識碼：A 文章編號：1673-9795（2014）02（c）-0055-01

1 數形結合概述

關于數形結合思想的說法有很多，不少教育理論界的專家指出：“數形結合不僅是一種原則和解題方法，同時還是一種數學意識和數學思想。”可見，數形結合思想在教育界中已經被廣泛認為是一種解決數學問題的思想，并且是一個值得教育分析、研究以及探索的理論觀點。從數學思想角度來講，數形結合可以被看作是一種數學意識，甚至可以被看作是一種科學意識。在數學教學活動中，教師要有針對性地培養學生的數形結合意識，使數形結合思想的作用得到最大限度地發揮，從而實現提高學生運用數形結合思想解決數學問題的能力的目的。

2 數形結合的類型

根據信息流向及數學轉化的方向，可以將數形結合分為三種類型：一是“化形為數”，即把幾何問題轉變成代數問題，然后利用解決代數問題的方法使幾何問題得到有效的解決。在實際問題解決過程中有代數法、解析法以及三角法等方法可以運用；二是“化形為數”法，即把代數問題通過有效的方法變成幾何問題，用解決幾何問題的方法使代數問題得到有效的解決，有構造輔助圖形法、圖像法等兩種比較常用的方法；三是“數型兼顧”法，即在具體的解決數學問題的過程中對數、形雙方給予高度的重視，使數與形二者進行相互地轉換，使數學問題得到有效的解決，有面積法、圖示法以及體積法三種比較常用的方法。

3 高中數學教學中運用數形結合思想的策略

3.1 善于培養學生運用數形結合思想解決數學問題的意識

在日常生活中，每個學生都有一定的圖形意識，如刻度尺與其上面的刻度、繩子與繩子上的結、每個學生的座位以及每天走過的路線等等，教師應充分利用學生具有的圖形意識，將數學中的數形結合思想的教學與學生生活中的形有效結合起來，有意識地培養學生的數形結合思想，提高學生解決數學問題的能力。如實數有無數個，主要包括正實數、負實數以及零，而直線是由無數個點組成的集合，二者之間具有共性，因此，實數可以用直線上的無數個點來表示，然后直線就被規定了正方向、單位長度以及原點，這條直線就被稱為數軸，數與直線上的點的結合得以建立。在數軸上每個數軸都有一個對應的點，數軸上的每個點都是實數，數軸上的點與實數之間的關系變得更加明確。

3.2 更新教學觀念，轉變學習方式

新課程標準指出，數形結合既不能作為一種解題工具，也不能僅重視數形結合解題的結果，直接教授學生數形結合的解題方法，卻忽視數形結合解題的分析探索過程。只有對數形結合的教育意義有一個充分的認識和了解之后，才更有利于在數學解題中運用數形結合思想，為學生數學解題能力的提高奠定良好的基礎，而這需要高中數學教師轉變教學觀念，也是充分發揮數形結合思想作用的重要前提條件。新課程還指出，學生的數學學習活動具有很多的可能性，除了讓學生利用接受、模仿、練習以及記憶的方式學習數學知識外，還需要積極地鼓勵學生嘗試更多學習數學的方式，如閱讀自學、合作交流以及自主探索等等。學生學習方式的轉變對實現數形結合的教學理念具有重要的促進作用。學生積極主動地探索數與形轉化的結合點有助于學生更好地運用數形結合的思想解決學習過程中遇到的數學難題。

3.3 重視分析數形結合思想解題出現的錯誤

在高中數學教學中，教師不僅要有意識地培養學生運用數形結合思想解決數學題的意識和能力，還要讓學生對數形結合方法解題過程中存在的問題給予高度的重視，這也是提高學生數學解題能力的重要途徑。教師指導學生認真分析數形結合解題錯誤并不是最終的教學目的，而是在充分認識和了解解題錯誤的基礎上找到出現錯誤的原因，然后認真改正自己的錯誤，避免學生在以后的數學解題過程中出現同樣的問題和錯誤，通過這樣的方法能夠使學生運用數形結合方法解決數學問題的能力得到很大的提高。此外，讓學生對數形結合解題的錯誤分析還有助于培養的思維能力、分析及解決問題的能力以及創新能力，從而實現培養學生糾錯意識及提高學生的數學學習效果和水平的目的。學生在數形結合解題過程中，致使出現解題錯誤的根本原因是數學轉化不等價，因此，教師應指導學生數學解題中數與形的轉化問題給予高度的重視，以實現提高學生解決數學問題效率的目的。例如題目：關于x的方程2x2-3x-2k=0在（-1，1）內有一個實根，則求k的取值范圍。

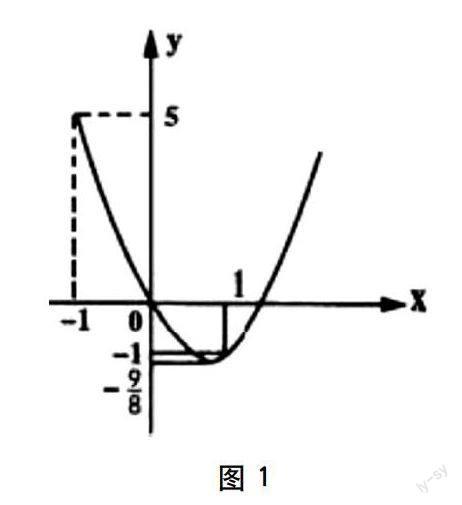
解析：將原方程變形為2x2-3x=2k后，即可轉化為求函數y=2x2-3x和函數y=2k的交點個數的問題。如圖1所示。

由圖1可知，隨著k的變化，當2k=-9/8或-1≤2k<5時只有一個公共點，即k=-9/16或-1/2≤k<5/2。學生如果利用數形結合，很容易就得出正確結果，否則不但解題過程繁瑣，還容易出現理解上的錯誤，如認為方程只有一個解等，從而使題目轉化不等價，無法得出正確答案。

4 結語

在高中數學教學中，教師要讓學生對數形結合這一數學思想的內涵有一個充分的認識和了解，使學生對數形結合思想給予高度的重視，還要讓學生充分理解和掌握數形結合的三種類型，使之能夠在實際解決過程中熟練地運用數形結合思想解決數學問題。此外，教師應明確地認識到培養學生數形結合意識的重要性，使學生從內心深處出重視數形結合思想和方法的運用，教師教學觀念的更新及學生學習方式的轉變能夠使學生的解題能力得到有效的提高。

參考文獻

[1] 李兆華.提高高中生數學解題能力的教學策略研究[D].東北師范大學，2006.

[2] 盧三國.提高高三學生數學解題能力的理論與實踐[D].華中師范大學，2006.

[3] 石紅芳.數學問題解決中的障礙成因分析及矯正對策研究[D].山東師范大學，2006.