中高職銜接的職業院校數學課程體系建設探討

李亞杰

摘要 在中高職銜接中，職業院校的數學課程設置既要符合職業教育人才培養要求，適應未來職業崗位的需求，又要為學生從技能型人才向高技能人才發展奠定學習基礎。經過多年的教學探索和改革，北京電子科技職業學院提出了“夯實基礎、融入專業、建設高職引領、中高職銜接”的數學課程建設理念，以加強基礎知識教學和技能訓練為中心任務，設計職業院校的數學課程體系。

關鍵詞 數學課程；職業教育；人才培養；中高職銜接；課程體系

中圖分類號 G712

文獻標識碼 A

文章編號 1008-3219（2014）23-0036-03

我國中高等職業教育并存，高職教育以培養高端技能型人才為目標，中職教育以培養高素質技能型人才為目標，不同層次職業教育的人才培養目標雖不盡相同，但存在共性，都是以培養技能型人才為首要目標。職業院校的數學課程設置既要符合職業教育人才培養規律，適應未來職業崗位的需求，又要為學生提供從技能型人才向高技能型人才轉型的學習基礎。經過多年的探索，北京電子科技職業學院在數學課程建設中加大改革創新力度，提出“夯實基礎、融入專業”的數學課程建設理念，以加強基礎知識教學和技能訓練為中心任務，按照職業教育特點和學校專業布局，逐步改變傳統數學課程設置和教學模式，構建了適用于學校高職三年制、高職五年制的數學課程體系。

一、確定數學課程的教改方向

北京電子科技職業學院的辦學定位是“依托首都經濟，面向京津冀，培養適應國際化企業和高端產業集群的高技能人才”。學校現有機械與數控、汽車與交通、自控與電氣、電子與信息、食品與生物、藝術與設計、經濟與管理七大專業群，覆蓋首都現代制造業、高新技術產業和現代服務業，在校學生由高職三年制和高職五年制兩部分組成。隨著職業教育理念的提升和學校專業布局的完成，專業課程教學改革不斷深入，文化基礎課程的教學改革緊隨其后。數學課程在教學內容設計上注重學生基礎知識掌握和基本技能訓練，并根據專業方向和未來工作崗位創建真實工作任務，注重學生基礎知識掌握和基本技能訓練，并將數學建模思想、數學實驗方法和具體工作任務融入到課程教學中。在教學過程中，根據各專業方向所涉及的典型工作任務，設計教學場景，構建虛擬仿真工作環境，在真實工作任務的場景中完成數學實踐教學，提高學生應用數學的能力，使數學真正成為后續職業課程教學的強有力支撐和未來職業工作必備的工具。

二、以高職為引領構建數學課程體系

高職引領數學課程，主要是針對高職三年制學生開設的數學課程。課程內容以“面向專業需求，建立數學基礎，融入建模思想，培養應用思維”為基本原則進行設計，分為《機電數學》《經濟數學》和《信息數學》三個教學方向，每個方向又分為基礎模塊、應用模塊和實踐模塊。基礎模塊重點講授微積分基礎理論知識，注重培養學生的基本邏輯思維和運算能力，該模塊為通用模塊；應用模塊根據專業方向的不同選取數學教學內容，為學生的后續學習奠定數學基礎；實踐模塊從專業和企業中選取典型工作任務（可動態調整）建立數學模型，并加以驗證和解決，培養學生分析和解決專業問題的能力。《機電數學》面向機械與數控、汽車與交通、自控與電氣以及生物工程專業群所涉及的各個專業開設；《經濟數學》面向經濟與管理專業群所涉及的各個專業開設；《信息數學》面向電子與信息專業群所涉及的各個專業開設。

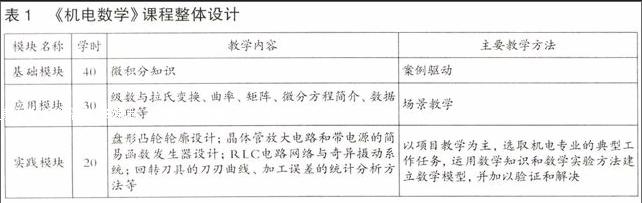
數學課程的開發、設計應當符合不同領域、不同職業工作的需要，尤其是要適應職業群體或行業的需要，根據高職不同專業的特點建構不同的高職引領課程，這是建構高職引領數學課程的最基本原則。以《機電數學》課程設計為例，在充分進行專業調研的基礎上，根據所需數學知識選取教學內容，并制定相應的課程標準，詳見表1。

三、中、高職數學課程銜接

（一）數學課程教學內容的銜接

1 高職三年制數學課程教學內容的銜接

高職三年制學生來源于中職、職高、高中，不但基礎有差異，而且學情也不同。任課教師首先應當了解、掌握所教班級學生的學習基礎和學情，可以通過摸底測驗或者問卷調查等方式進行。在全面掌握學生學習基礎和學情的基礎上，進行課程的整體設計和每個單元的教學設計。在內容上采取“溫故知新”的方式，實現中、高職數學學習內容的銜接，包括一些基本概念和基本定理、公式。

2 高職五年制數學課程教學內容的銜接

高職五年制（中高職連讀）的數學課程設置是在前三年完成中職階段的學習，后兩年完成高職階段的學習，并在第三年進行由中職階段向高職階段的轉段分流。學校根據學制特點和人才培養規格，將高職五年制數學課程分為《初等數學》和《應用數學》兩個模塊。《初等數學》是中職階段數學教學模塊，《應用數學》是高職階段數學教學模塊，也分為機電、經濟和信息三個方向，即在前兩年面向各專業學生開設《初等數學》課程，第三年對轉段進入高職學習的學生根據不同的專業方向開設《應用數學》課程，實現了中、高職數學課程的有效對接，達到“高職引領，中高職銜接”的高職五年制課程建設目標。

（二）中高職數學課程思維模式的銜接

思維模式多種多樣，可區分為理性思維和形象思維，或者分為理論思維和實踐思維。思維模式決定著學習風格和學習模式。高職數學教學在傳授數學知識的同時，必須培養數學思維能力。

培養數學思維能力有兩種方式：邏輯歸納法和邏輯演繹法。理性思維強的人，可以比較好的運用邏輯演繹法；而理性思維不強的人，則宜采用邏輯演繹法。對于高職生而言，無論是三年制，還是五年制，在傳授理論時，最好采用邏輯歸納法，即從具體的數學事件或者具象出發，通過分析歸納出概念、理論。相對于三年制高職生，五年制學生的理性思維能力或者理論思維能力更弱，就更需要從具體的數學事件或者具象出發，運用邏輯歸納法，不斷提升其數學思維的能力，并且培養他們運用數學的意識。

（三）中高職數學課程教學模式的銜接

傳統的中等學校數學教學模式都是講練結合的模式和邏輯演繹模式。對于職業院校的學生，應當采用溫故知新的教學模式。溫故知新，并非簡單重復、羅列初等數學的概念、定理和公式等，而要和高職數學發生聯系。所以，在教學模式上要有所提升，例如，用案例分析-歸納-理論-演繹-解決問題的教學模式，使高職數學教學模式與中等學校數學教學模式銜接起來，并有所發展。

（四）中高職數學課程教學策略的銜接

教學策略主要包括教學方法、教學手段、教學表達策略等。三年制高職生來源于三校生，與本科生相比，其依賴性比較突出，抽象思維、理論思維比較弱；而中職生在這些方面更加明顯。因此，在教學策略上，要更突出強調理論聯系實際，強調啟發式教學、師生互動式教學，特別是案例驅動、場景教學、建模和上機操作。通過這些教學策略，逐步培養學生學習的主動性和獨立性，提高學習及運用數學的自我意識和能力。

總之，《初等數學》和《應用數學》兩門課程的關系，是前置和后續的密切聯系。在《應用數學》教學之始，先以師生互動的形式系統復習初等函數等知識，有效地完成中職與高職數學課程知識的銜接。在教學模式上，多采用直觀的形式進行教學導入，運用案例驅動、數學實驗、建模方法以及專業問題的數學建模處理等教學方法和手段。在每個教學項目開始，根據專業實例或生活實例，闡述項目的實際應用和價值，調動學生學習的興趣和積極性，同時，復習《初等數學》基礎知識，進行課程的教學導入。在教學進程中，加強師生討論和互動，并采用多種靈活的方式、實施發展性評價，形成生動活躍的“教、學、做、練、評”一體化教學情境。

四、實施效果

經過幾年建設，學校數學課程體系日趨完善，在三年制（藝術類除外）和五年制各專業的數學課程教學中收到了良好效果，為學生后續專業的學習打下了堅實基礎，解決了困擾高職數學多年的“教什么、怎么教”的瓶頸問題。由于數學課程建設理念和教學實施效果的示范作用，學校于2012年被北京市教育委員會批準為“北京市職業院校數學教師培訓試點項目”建設單位，負責北京市職業院校數學師資的培訓任務，在全市范圍內推廣學校的數學課程建設成果。