基于Monte–Carlo模擬法的投資項目風險分析

龔婭　雷健鋒　余蓉

[摘 要]本文對蒙特卡羅模擬法的分析步驟作了簡要介紹，并就其在風險分析中的應用進行了舉例說明。運用蒙特卡羅模擬技術分析評價了項目的主要風險因素，通過對模擬結果的分析，對方案的抗風險能力進行分析，為項目的決策提供有力的依據。最后，結合實例研究驗證了蒙特卡羅模擬在投資項目風險評價中的可行性及有效性。

[關鍵詞]蒙特卡羅模擬；風險分析；凈現值

[DOI]10.13939/j.cnki.zgsc.2015.43.033

1 引 言

項目風險評估是項目評估的重要內容，通過風險評價，可以判定項目的風險程度，決策者就能夠正確認識和面對風險，做出取得合理風險報酬的正確決策，是項目經濟評價不可或缺的重要組成部分。項目風險評估是微觀經濟和宏觀經濟理論在投資決策與管理領域的具體應用，評估方法合理化和科學化是投資決策的前提條件。目前我國在風險投資決策理論研究中，對風險投資項目的風險評價方法的局限性在于主觀性較強，難以保證結果的準確性。本文在現有研究成果的基礎之上，利用蒙特卡羅模擬技術對某項目方案進行評價，能夠克服主觀因素的缺陷，通過結果分析，驗證了此技術在投資項目風險評價應用的有效性。

2 項目投資風險的Monte-Carlo模型

利用蒙特卡羅模擬法對項目經濟評價指標進行風險分析的步驟和具體內容如下。

2.1 建立評價指標模型并對風險變量進行風險分析

設經濟評價指標為y，經濟分析確定的風險變量為x1，x2，…，xn，根據經濟評價理論和投資方案的系統分析，不難確定：

y=f（x1，x2，…，xn）

或

φ（y，x1，x2，…，xn）=0

對風險變量進行風險分析給出每一風險變量的概率分布及概率特征值，確定變量之間的相關程度。

2.2 確定隨機數與風險變量取值的對應關系，抽樣并產生樣本值

2.2.1 隨機數

隨機數有兩類，均勻分布的隨機數（一般簡稱隨機數）和隨機標準正態偏差。

如果所模擬的分布是正態分布（或者是分裂￣正態分布），因為標準正態分布能代表所有這樣的分布，所以可以利用標準正態偏差進行簡化計算。

2.2.2 確定隨機數的風險變量取值對應關系

（1）風險變量是離散分布。當風險變量為離散分布時，可按由離散分布、累計分布、累計概率標度、隨機數、變量樣本值的順序取得變量樣本值。

（2）風險變量是連續分布。當變量為階梯矩形分布時，它的累計概率分布是由一系列線性部分組成的，從這種分布抽樣的方式和對離散分布抽樣的方式完全相同，因為結果是連續分布的，所以根據累積概率分布曲線可以確定結果的樣本值，為了得到樣本的準確值，可在相應區間使用直線插值法求解。當變量為均勻分布時，顯然根據累積分布曲線可直接得到變量的樣本值。用數學方法表示如下：

樣本值=[SX（]a+b[]2[SX）]-[SX（]b-a[]2[SX）]+[SX（]R·N[]R·N·m[SX）]（b-a）

式中，R·N表示已知位數的任意隨機數；R·N·m表示已知位數的最大隨機數。

奇特連續分布可采用類似的方法建立對應關系和抽取樣本。

（3）風險變量是正態分布（或分裂正態分布）。當變量是正態分布時，可利用標準正態偏差求得每一變量的樣本值。

樣本值=期望值+隨機標準正態偏差×標準差

如果是分裂正態分布，利用最適值或眾數作分界線，把模擬樣本分為兩組，則可采用正態分布同樣的分析方法，確定隨機正態偏差對應的樣本值。

（4）相關問題的處理。通常評價指標的風險變量有多個，當變量相互獨立時，各變量分別進行隨機模擬抽樣，即取不同的隨機數確定樣本值。當兩個變量完全相關時，應取相同的隨機數確定樣本值。當變量相關時（指0<[JB（|]ρ[JB）|]<1，ρ為相關系數），如果能通過相關分析，確定其中一個變量對于另一變量的條件概率分布，那么可以取同一隨機數確定一個變量的樣本值和根據條件概率分布確定另一變量的樣本值。

2.3 求解經濟評價指標模擬值

將得到的各變量的樣本值輸入已建立的評價模型，借助現代計算工具，求解評價指標的模擬值。有多少組變量的樣本值，就可以得到同樣多數目的評價指標模擬值。

2.4 給出評價指標的概率分布、期望值和標準差

2.4.1 概率分布

匯總、整理n次模擬結果可得到評價指標的頻率分布表和頻率分布圖，累計概率分布表和累計概率分布圖。

2.4.2 期望值和標準差的計算

如果模擬結果未經加工整理，則

E（y）=[AKy-]=[SX（][DD（]n[]i=1[DD）]yi[]n[SX）]

σy=[KF（][SX（]1[]n[SX）][DD（]n[]i=1[DD）]（yi-[AKy-]）2[KF）]

式中，yi表示第i次模擬值（i=1，2，…，n）。

如果模擬結果經過分組處理，組數為k，則

E（y）=[AKy-]=[DD（]k[]i=1[DD）]yi·pri

σy=[KF（][DD（]k[]i=1[DD）]（yi-[AKy-]））2·pri[KF）]

式中，yi、pri表示第i組的模擬值（組中值）和頻率（i=1，2，…，k）。

2.5 模擬結果的準確性檢驗

用蒙特卡羅法分析評價指標時，模擬次數越多，就能得到更客觀、更正確的結果。但模擬次數越多，成本也會相應增加。因此，應確定最適當的模擬次數以期達到最好效果。

模擬實驗證明，當模擬進行一定次數后，得到的結果漸漸趨于穩定，此時誤差很小。因此模擬次數的確定可考慮以下因素：①模擬結果與真實結果的誤差是否滿足評價結果的精度要求；②模擬特征值是否圍繞某一個值波動且趨于穩定；③與其他方法的結果進行比較分析。

2.6 風險評價

蒙特卡羅模擬給出了能代表評價指標真實分布的概率分布，因此能確定在任意置信區間下評價指標下的下限（或上限）或在一定臨界指標下經濟虧損（或盈利）的概率。

3 案例分析

A企業是一家飲料企業，現準備投資一種新型果汁飲料開發的項目，該項目的初始投資額為500萬元。該項目如果投入運營，第一年產品的銷量將是一個服從均值為400萬件而標準差為80萬件的正態分布，根據這種產品的生命周期規律，第二年銷量將在第一年的基礎上增長30%，而第三年銷量將在第二年基礎上增長-20%。三年內每年還需投入固定成本120萬元。新果汁產品的單位變動成本在1～3元均勻分布。委托咨詢機構對產品銷價的市場調研結果如表1所示。將此投資項目的貼現率定為10%，分析此投資項目的風險如下：

（1）建立模型和評價指標。蒙特卡羅模擬法最常用的是通過模擬計算凈現值來評估項目的投資風險，凈現值等于未來現金流的折現值與項目投資成本的差額。一般來說，凈現值越大越好，當NPV>0時，投資方案可接受；NPV<0時，投資方案不可接受。凈現值的表達式為：

NPV=[DD（]n[]t=1[DD）]（CI-CO）t（1+i）-t

式中，（CI-CO）t—第t年的凈現金流量；i—設定的折現率；n為項目計算期。

（2）對案例已知的數據進行簡單的整理。據分析有九個固定數值的輸入參數和三個不可控的輸入參數，如表2所示。

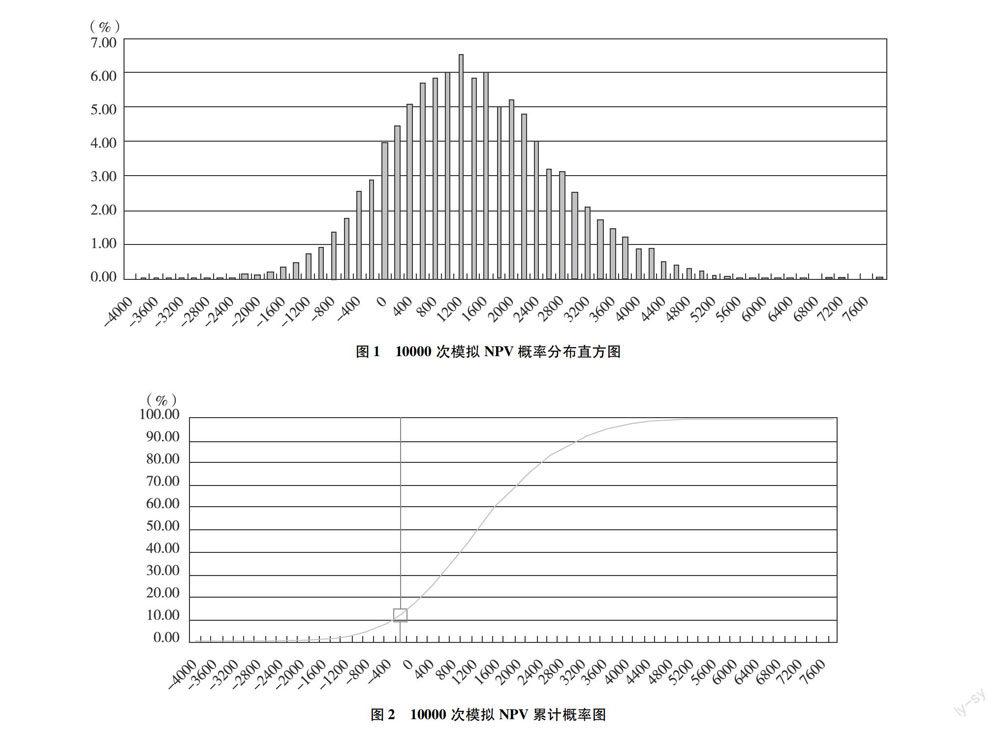
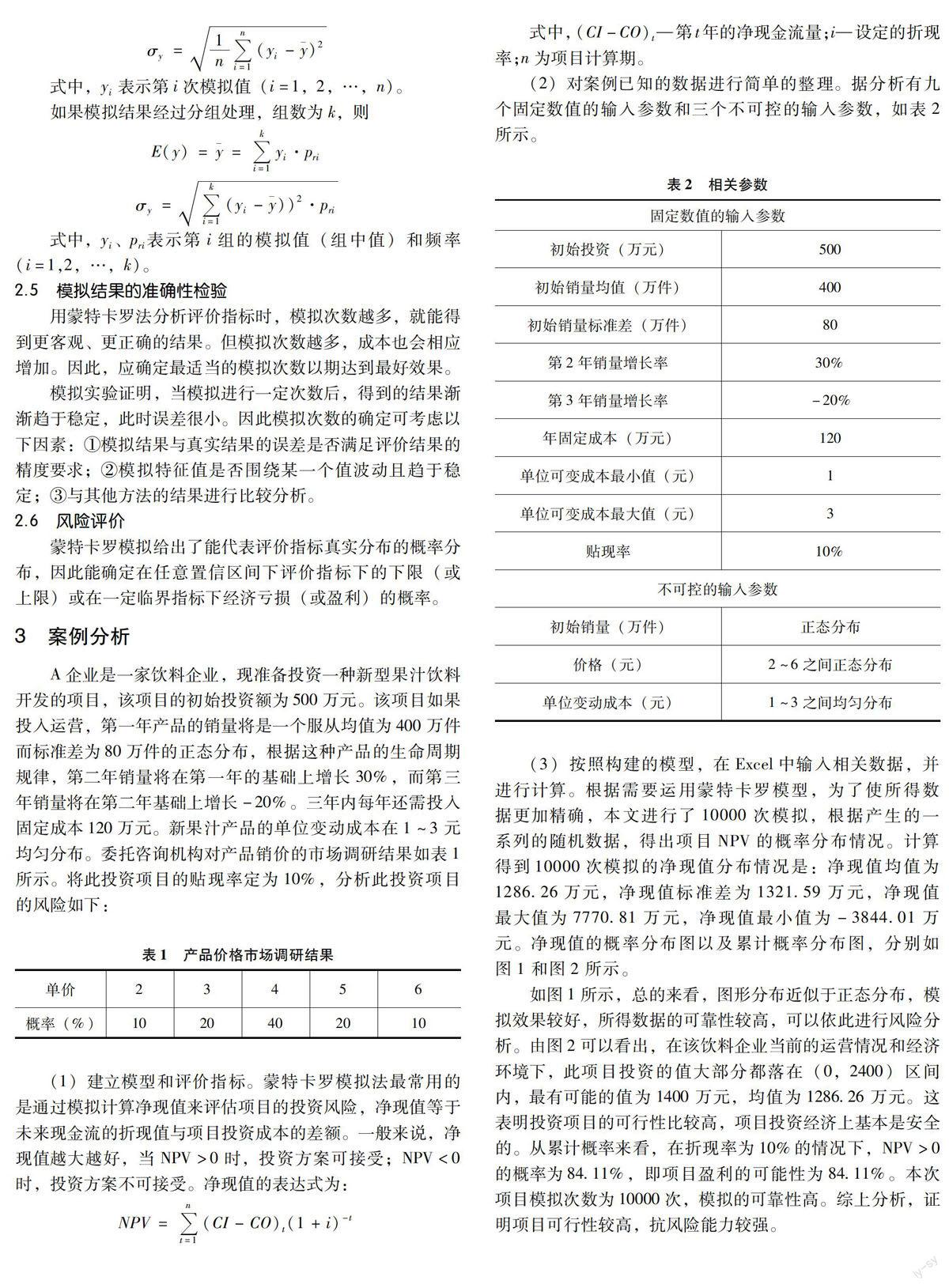
（3）按照構建的模型，在Excel中輸入相關數據，并進行計算。根據需要運用蒙特卡羅模型，為了使所得數據更加精確，本文進行了10000次模擬，根據產生的一系列的隨機數據，得出項目NPV的概率分布情況。計算得到10000次模擬的凈現值分布情況是：凈現值均值為1286.26萬元，凈現值標準差為1321.59萬元，凈現值最大值為7770.81萬元，凈現值最小值為-3844.01萬元。凈現值的概率分布圖以及累計概率分布圖，分別如圖1和圖2所示。

如圖1所示，總的來看，圖形分布近似于正態分布，模擬效果較好，所得數據的可靠性較高，可以依此進行風險分析。由圖2可以看出，在該飲料企業當前的運營情況和經濟環境下，此項目投資的值大部分都落在（0，2400）區間內，最有可能的值為1400萬元，均值為1286.26萬元。這表明投資項目的可行性比較高，項目投資經濟上基本是安全的。從累計概率來看，在折現率為10%的情況下，NPV>0的概率為84.11%，即項目盈利的可能性為84.11%。本次項目模擬次數為10000次，模擬的可靠性高。綜上分析，證明項目可行性較高，抗風險能力較強。

4 結 論

本文根據項目投資風險的特點，運用蒙特卡羅模擬方法對風險項目進行風險評價。文中模型采用簡化參數的概率假設，使整個模擬過程得到簡化。并且，它是一種處理多變量變化的方法，充分考慮了各因素各種取值或值域發生的概率，克服了傳統敏感性分析方法受單個變量單獨變化的局限性，又使結果不失可信度。因此，通過對模擬結果的分析，對方案的抗風險能力進行判斷，可以辨識明顯不具備投資條件的項目，為項目投資者提供了有力的依據。

參考文獻：

[1]Fang C，Marle F，Zio E，et al.Network Theory-based Analysis of Risk Interactions in Large Engineering Projects[J].Reliability Engineering & Systm Safety，2012（106）：1-10.

[2]Chao Fang，Franck Marle.Dealing with Project Complexity by Matrix-based Propagation Modelling for Project Risk Analysis[J].Journal of Engineering Design，2013，24（4）：239-256.

[3]Ghafari M，Safakish G，Sheikhahmadi F.Modeling and Risk Analysis of Virtual Project Team through Project Life Cycle with Fuzzy Approach[J].Computer & Industrial Engineering，2014，72（3）：98-105.

[4]Gingnell L，Franke U，Lagerstrom R，et al.Quantifying Success Factors for IT Projects-an Expert-based Bayesian Model[J].Information Systems Management，2014，31（1）：21-36.

[5]肖建，譚勝，袁繼國.科技創業企業的風險投資項目價值評估模型[J].財經科學，2008（7）：79-85.

[6]吳金美，金治明，凌曉冬.風險投資的多階段復合實物期權定價方法[J].數學的實踐與認識，2010（9）：31-36.