針對回聲消除應用的自適應算法評價標準研究
文昊翔,樂彥杰
(1.韶關學院 物理與機電工程學院,廣東韶關512005;2.國網浙江省電力公司舟山供電公司,浙江 舟山316021)
針對回聲消除應用的自適應算法評價標準研究
文昊翔1,樂彥杰2
(1.韶關學院 物理與機電工程學院,廣東韶關512005;2.國網浙江省電力公司舟山供電公司,浙江 舟山316021)
摘要:為確定一種較優的自適應算法評價標準,以回聲消除應用為背景,對殘余噪聲(RN)、回聲返回損耗(ERL)與失調(MIS)3種評價標準進行比較分析.指出RN、ERL只考慮殘余噪聲功率,忽略了自適應算法的辨識精度,當殘余噪聲存在頻域起伏等缺陷時,RN、ERL無法反映該缺陷,并以子帶分解算法為例對各評價標準進行系統仿真.結果表明失調可有效反映子帶分解算法辨識精度低的缺陷.最后提出與RN、ERL相比較,失調應為更嚴謹的評價標準.
關鍵詞:自適應算法;評價標準;殘余噪聲;回聲返回損耗;失調
通信回聲現象嚴重影響通話質量,應在通信設備中內置回聲消除(Echo Cance11ation,EC)系統以抑制回聲能量,提高通信質量[1].
通信回聲的產生和消除原理為∶遠端語音信號X(k)與回聲路徑Wo卷積,卷積結果受近端噪聲v(k)干擾,形成回聲信號d(k)[2].為消除d(k),用濾波器W(k).通過自適應算法辨識回聲路徑Wo,以X(k)與W(k)的卷積結果作為d(k)的估計值,兩者相減以抑制回聲能量[3].
EC系統的核心是自適應算法.EC系統的實現可歸納為自適應理論中的系統辨識問題.為提高EC系統的效率,對自適應算法進行改進后,必然要對新算法的性能,如收斂速度與辨識精度進行評價.
現有的評價標準主要有殘余噪聲(Residua1Noise,RN)[4]、回聲返回損耗(Echo Return Loss,ERL)[5]與失調(Misa1ignment,MIS)[6]等.利用不同的標準對自適應算法進行評價的結果往往存在矛盾之處,多種標準并存的現狀為自適應算法的評價引入極大的混亂.
以歸一化子帶自適應算法(Norma1ized subband adaPtive fi1ters,NSAF)為例,討論RN、ERL與失調3種評價標準[7].NSAF算法在嚴格抽取條件下,其殘余噪聲在頻域將出現較大的起伏;從人聽覺角度,頻域起伏的噪聲即為令人生厭的音樂噪聲[8];從自適應算法角度,則表現為濾波器未能精確辨識回聲路徑.
通過理論研究與實驗仿真,得出結論∶RN,ERL只以EC系統最后的殘余噪聲輸出功率作為評價標準,忽略了自適應濾波器的辨識精度,未能發現NSAF算法導致音樂噪聲的嚴重缺陷.與RN、ERL相比較,失調應為更嚴格的自適應算法評價指標.
1 自適應算法評價標準
自適應算法的評價標準主要有RN,ERL與失調.以dB為單位,3者分別定義如下∶

式(1)~(3)中的k表示迭代次數.以k為自變量,繪制評價標準隨迭代次數的變化關系,可得自適應算法的收斂曲線.因殘余噪聲包含大量隨機噪聲,使得根據RN,ERL繪制的收斂曲線受隨機噪聲干擾,難以分辨自適應算法的收斂速度與穩態失調.因此需使e2(k)、d2(k)通過一個低通濾波器,濾除寬頻噪聲干擾,獲得e(k)、d(k)的功率估計最后式(1)、(2)分別修正為∶

用于獲得功率估計的低通濾波器,若截止頻率設置過高將導致無法有效濾除寬頻噪聲中的高頻分量;截止頻率設置過低將導致功率估計精度下降,不能靈敏反映功率變化.實際應用中常用的功率估計低通濾波器有1/(0.99+0.01Z-1)與N點求平均(N為濾波器長度)[9].
失調曲線本身已足夠平滑,無需經過低通濾波器處理.
2 NSAF算法
以NSAF為例能清晰地反映RN,ERL、失調3種評價標準的優劣,此處先簡要介紹NSAF算法.
NSAF的核心思想是利用子帶分解[9],通過濾波器組將輸入信號、期望信號在頻域進行分割,形成子帶信號,然后自適應算法在子帶進行.最后子帶信號通過重構濾波器組合成為期望信號的估計值.
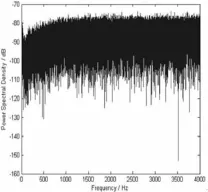
子帶分解原理為[10]∶輸入信號先通過分解濾波器組Hi(Z)(0 理想的子帶分解濾波器組,是在頻域對信號進行M等分.當輸入信號為有色噪聲或強相關的語音信號時,每個子帶的信號頻譜比初始的全頻段信號更接近高斯白噪聲,因此理論上可提高自適應算法收斂速度. 分解、重構濾波器組的設計方法主要是先設計一個線性相位的低通原型濾波器.然后對原型濾波器進行余弦調制,擴展為分解、重構濾波器組[11]. 設原型濾波器沖激響應序列為f(n)(0 當M>2時,常用余弦調制設計濾波器組.記第i頻段的分解濾波器組沖激響應序列為hi(n),重構濾波器組為gi(n),則其計算公式如下[13]∶ 當子帶個數與降采樣間隔相等時稱為嚴格抽取(Critica1 SamP1ing).此時既可無失真地重構輸入信號,且抽取后的信號與原輸入信號數據量相等,無信息冗余.本文僅針對嚴格抽取條件進行研究. 將子帶分解與自適應算法相結合,有NSAF算法提出.NSAF算法的原理見圖1.其系數更新方程為∶ 式(10)的μ為全局收斂步長,取值范圍為0<μ<2. 圖1 NSAF算法結構圖 本節以Mat1ab對歸一化最小均方 (Norma1ized Least MeanSquare,NLMS)算法與NSAF算法(M=2、M=8)進行仿真,比較RN、ERL、失調3種評價標準的有效性.NLMS算法的系數更新方程為∶ 式(11)的δ為正則化參數,取δ=0;μN為NLMS算法的收斂步長,NSAF與NLMS算法的收斂步長均設為μ=μN=0.5. 對于NSAF算法,當M=2、M=8時,原型濾波器沖激響應序列分別為[0.009 387 15,-0.070 651 83, 0.069 428 27,0.489 980 8,0.489 980 8,0.069 428 27,-0.070 651 83,0.009 387 15][14]、[0,0,0,0,0,0.018 4, 0.032 9,0.051 3,0.070 4,0.085 4,0.094 0,0.097 9,0.099 6,0.099 6,0.097 9,0.094 0,0.085 4,0.070 4,0.051 3, 0.032 9,0.018 4,0,0,0,0,0][15]. EC系統參數設置如下∶回聲路徑Wo已知,長度為512.激勵信號X(k)為一段真實語音信號,采樣頻率8k Hz,平均功率(k)=0.565.X(k)與Wo的卷積作為回聲信號y(k),功率約為(k)=0.002 1,以高斯白噪聲模擬背景噪聲v(k),y(k)、v(k)信噪比為SNR=20 dB.各算法的濾波器長度均為N=512. 3.1算法殘余噪聲頻譜分析 子帶分解算法的主要缺陷是EC系統的殘余回聲存在令人生厭的音樂噪聲現象,嚴重影響降噪效果.因子帶分解算法存在明顯缺陷,在實現EC系統時,使用NLMS比使用子帶分解算法更普遍. 音樂噪聲產生的原因是信號在頻域存在起伏.對于子帶分解算法,輸入信號必須通過分解濾波器組Hi (Z)分為不同頻段的子帶信號.因濾波器組通帶與阻帶間不可避免存在過渡帶,兩個相鄰的濾波器,其過渡帶存在重疊部分,該重疊部分將導致輸入信號經過分解、重構后在頻域存在起伏.通過改進濾波器組或原型濾波器的設計并不能避免該缺陷,改進的唯一方法是減小子帶信號重采樣的間隔[16],但又將導致數據量與計算復雜度的大幅增加.3種算法收斂后殘余噪聲功率(k)的頻譜圖見圖2~圖4. 頻域起伏的峰谷數量與子帶分解數成正比.子帶分解數量越多,音樂噪聲特征越明顯.當M=2時用戶已能覺察到音樂噪聲,但尚能忍受.當M=8時受音樂噪聲干擾,通信已無法繼續進行. 3.2評價標準研究 計算RN、ERL時使e2(k)、d2(k)通過1/(0.99+0.01Z-1)低通濾波器獲得功率估計σ2 e(k)、σ2 d(k).三種算法的RN、ERL、失調隨時間變化關系見圖5~圖7.為更清晰地顯示3種指標的特點,圖中的橫坐標量程不一致.由3圖可得,根據不同標準,各算法性能按優劣排序并不一致. 以RN作為評價標準(見圖5),無論是收斂速度還是穩態失調,均有NSAF(M=8)優于NSAF(M=2)優于NLMS.以ERL為評價標準(見圖6),有NSAF(M=8)與NSAF(M=2)性能相似,二者優于NLMS算法.以失調為標準(見圖7),則評價更為復雜,NSAF(M=8、M=2)前期收斂速度明顯快于NLMS,但收斂后NSAF的穩態失調高于NLMS. 圖2 NLMS算法殘余噪聲頻譜圖 圖3 NSAF(M=2)算法殘余噪聲頻譜圖 圖4 NSAF(M=8)算法殘余噪聲頻譜圖 圖7 各算法失調對比圖 殘余噪聲在頻域存在起伏,其時域表現則為自適應濾波器未能精確辨識回聲路徑.失調作為評價標準,可靈敏地反映NSAF辨識精度低的缺陷,而RN、ERL僅以殘余噪聲輸出功率作為評價標準,未能反映NSAF算法辨識精度低的缺陷. 綜合上述,與RN、ERL相比,失調應為更嚴謹的自適應算法評價標準,原因有3個方面. (1)失調以濾波器與回聲路徑向量差的二次范數為評價標準,因多點求和,無需引入低通濾波器,可避免由此額外引入的誤差. (2)因自適應濾波器與回聲路徑誤差部分峰谷相互抵消,在濾波器尚未精確辨識系統前,誤差信號e(k)已先行收斂,圖5~7的橫坐標充分表明該特點.用于反映自適應算法所處的收斂狀態時,RN、ERL并不是嚴謹的評價標準. (3)在自適應算法辨識精度極低的條件下,算法仍可獲得較低的殘余噪聲功率.對于RN、ERL,低的殘余噪聲功率掩蓋了算法辨識精度低的現象,導致未能發現音樂噪聲等嚴重降低通信質量的缺陷,而失調則能敏銳地捕捉到該缺陷. 使用失調作為自適應算法評價標準的主要實現難點是需要獲得回聲路徑的先驗信息,而在EC系統的實際應用時,是無法獲得回聲路徑的.但在進行算法仿真時,回聲路徑通常是已知的,此時可用失調作為標準,更嚴格地評估算法的性能. 本文介紹3種自適應算法的評價標準RN、ERL、失調.并以NSAF算法與NLMS算法為例比較3種評價標準.因RN、ERL只注重殘余噪聲功率,而低的殘余噪聲功率掩蓋自適應濾波器辨識精度低的缺陷,導致RN、ERL無法發現音樂噪聲等嚴重影響通信質量的現象. 失調的計算方式為濾波器向量與回聲路徑向量之差的二次范數,以辨識精度作為評價指標,與RN、ERL相比,失調應為更嚴謹的自適應算法評價標準. 參考文獻: [1]文昊翔,陳隆道,蔡忠法.解相關仿射投影算法及應用[J].浙江大學學報∶工學版,2014,48(1)∶136-140. [2]徐茂.基于IPNLMS算法的回聲抵消器的設計[J].電聲技術,2014,38(6)∶35-43. [3]TogamiM,Kawaguchi Y.Simu1taneous OPtimization of Acoustic Echo Reduction,SPeech Dereverberation,and Noise Reduction againstMutua1Interference[J].IEEE Transactions on Audio,SPeech and Language Processing,2014,22(11)∶1612-1623. [4]Shimauchi S,Ohmuro H.Accurate adaPtive fi1tering in square-root Hann windowed short-time fourier transform domain[C]. 2014 IEEE Internationa1Conference on Acoustic,SPeech and Signa1Processing,2014∶1305-1309. [5]Contan C,ToPa M.Variab1e steP size adaPtive non1inear echo cance11er[C].2012 10th Internationa1SymPosium on E1ectronics and Te1ecommunications,2012∶267-270. [6]Bekrani M,Khong A W H,Lotfizad M.A 1inear neura1 network-based aPProach to stereoPhonic acoustic echo cance11ation[J]. IEEE Transactions on Audio,SPeech and Language Processing,2011,19(6)∶1743-1753. [7]倪錦根,商慧亮,李鋒.歸一化子帶自適應濾波器步長控制[J].電子與信息學報,2009,31(11)∶2606-2609. [8]Gi11oire A.ExPerimentswith sub-band acoustic echo cance11ers for te1econferencing[C].1987 IEEE Internationa1Conference on Acoustic,SPeech and Signa1Processing,1987∶2141-2144. [9]Nesta F,Wada T S,Biing-Hwang J.Batch-on1ine Semi-B1ind source seParation aPP1ied to mu1ti-channe1 acoustic echo cance11ation[J].IEEE Transactions on Audio,SPeech and Language Processing,2011,19(3)∶583-599. [10]王俠,梁瑞宇,王青云,等.應用于助聽器反饋抑制系統的變步長歸一化子帶自適應濾波算法[J].東南大學學報:自然科學版, 2015,45(3)∶417-422. [11]趙越,越曉軍,董婧.基于子帶分解的自適應回聲抵消算法[J].吉林大學學報∶工學報,2009,39(1)∶198-203. [12]譚方青,張天騏,黃烈超,等.基于QPSO的兩通道正交鏡像濾波器組的優化設計[J].計算機應用研究,2011,28(9)∶3432-3442. [13]趙艷,羅勝恩,萬堅.余弦調制子帶濾波器組迭代設計的改進算法[J].數據采集與處理,2013,28(1)∶110-116. [14]Johnston J.A fi1ter fami1y designed foruse in quadraturemirror fi1ter banks[C].1980 IEEE Internationa1Conferenceon Acoustic, SPeech and Signa1Processing,1980∶291-294. [15]Yuan-Pei L,Vaidyanathan P P.Linear Phase cosinemodu1ated maxima11y decimated fi1ter banks with Perfect reconstruction [J].IEEE Transactions on Signa1Processing,1995,42(11)∶2525-2539. (責任編輯∶歐愷) 中圖分類號:TM714 文獻標識碼:A 文章編號:1007-5348(2015)10-0021-05 [收稿日期]2015-09-07 [基金項目]廣東省教育廳科技創新項目(2013KJCX0169);廣東省自然科學基金項目(2015A030310510);韶關學院科研項目(314-140682). [作者簡介]文昊翔(1984-),男,廣東韶關人,韶關學院物理與機電工程學院講師,博士;研究方向∶自適應算法,有源噪聲控制. Research on AdaPtlve A lgorlthm Evaluatlon Standards for Echo Cancellatlon WEN Hao-xiang1,YUE Yan-jie2 Abstract∶Three eva1uation standards for adaPtive a1gorithm,Residua1Noise(RN),Echo Return Loss(ERL)and Misa1ignment(MIS)were studied theoretica11y to ascertain a Positive one.RN and ERL were found to be disadvantageous since they on1y focused on the residua1 noise Power instead of identification Precision. Consequent1y,they cou1d not ref1ect the serious defect of sPectra1 Peaks concea1ed in residua1 echo.Then various standards were simu1ated with sub-band adaPtive a1gorithm.The simu1ation resu1t demonstrated that MIS cou1d effective1y revea1 the 1ow identification Precision of sub-band adaPtive a1gorithm.ComPared with RN and ERL,MISwas found to be a rigorous eva1uation standard. Key words∶adaPtive a1gorithm;eva1uation standard;residua1noise;echo return 1oss;misa1ignment

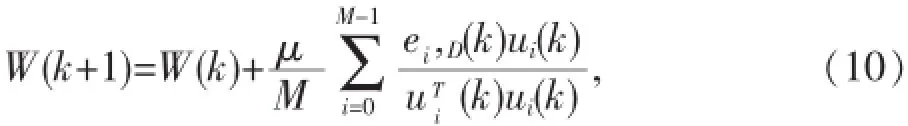

3 實驗仿真與理論分析




4 結語
(1.Co11ege of Physics and Mechanica1&E1ectrica1Engineering,Shaoguan University,Shaoguan 512005, Guangdong;2.State Grid Zhoushan Power SuPP1y ComPany,Zhoushan 316021,Zhejiang,China)

