本原性教學(xué)：數(shù)學(xué)教學(xué)的理性回歸

趙兆兵

[摘 要]“本原性教學(xué)”意味著教學(xué)回歸“本原”，追問教學(xué)的本質(zhì)，這不僅是對數(shù)學(xué)教學(xué)現(xiàn)實(shí)的一種糾偏，更是對學(xué)科教學(xué)深層的本質(zhì)性的一種追尋。它是一種教學(xué)的方式，一種教學(xué)設(shè)計(jì)的理念，也是一種思考教學(xué)的方式。本原性教學(xué)的課堂實(shí)踐要立足數(shù)學(xué)視野，分析教學(xué)內(nèi)容；站到兒童立場，構(gòu)建整體框架；回到教學(xué)場域，把握關(guān)鍵事件。

[關(guān)鍵詞]本原 數(shù)學(xué)教學(xué) 教學(xué)內(nèi)容 整體框架 關(guān)鍵事件

[中圖分類號] G623.5 [文獻(xiàn)標(biāo)識碼] A [文章編號] 1007-9068（2015）29-012

夏丏尊先生在《愛的教育》譯者序言中有這樣一段文字：“學(xué)校教育到了現(xiàn)在，真空虛極了。單從外形的制度上、方法上，走馬燈似的變更迎合，而于教育的生命的某物，從未聞有人培養(yǎng)顧及。好像掘池，有人說四方形好，有人又說圓形好，朝三暮四地改個(gè)不休，而于池的所以為池的要素的水，反無人注意。”夏先生在這里說的是教育，其實(shí)，數(shù)學(xué)教學(xué)又何嘗不是如此！過分追求教學(xué)外在的“形式”，而不關(guān)注教學(xué)內(nèi)容的本質(zhì)，只為演繹所謂“教”的精彩，而不關(guān)心學(xué)生真實(shí)的想法，一味跟風(fēng)模仿，迎合新的理念，缺少自己獨(dú)立的價(jià)值判斷與理性思考，教學(xué)正與我們的“初衷”漸行漸遠(yuǎn)，變成一個(gè)“沒有了水的池塘”。“洞見或透識隱藏于深處的棘手問題是很難的，因?yàn)槿绻皇前盐者@一棘手問題的表層，它就會維持原狀，仍然得不到解決。因此，我們開始以一種新的方式來思考。”顯然，數(shù)學(xué)教學(xué)亟需回歸本原，追尋本原性的學(xué)科教學(xué)！

一、數(shù)學(xué)“本原性教學(xué)”的內(nèi)涵詮釋

“本原”字典中的解釋是根本，事物的最重要部分。哲學(xué)上指萬物的最初根源，世界的來源和存在的根據(jù)。哲學(xué)中對“本原”的思考表現(xiàn)為一種刨根問底的探詢精神，始終把理解世界的“終極存在”、“始基”、“初限”或構(gòu)成世界的“元素”作為哲學(xué)研究中的首要問題。

借用哲學(xué)中對“本原”的理解和思考方式，我們嘗試提出一種“本原性教學(xué)”的設(shè)想，即教師始終把某個(gè)數(shù)學(xué)問題中最為原始、樸素、本質(zhì)的觀念、思想和方法作為思考的首要問題。緊扣教學(xué)內(nèi)容的數(shù)學(xué)本質(zhì)設(shè)計(jì)教學(xué)任務(wù)，引導(dǎo)學(xué)生在交往互動的過程中獲得知識建構(gòu)和能力提升，形成良好學(xué)科觀念的一種教學(xué)方式。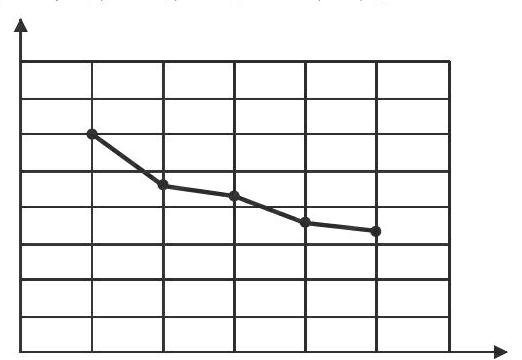

作為一種理想的教學(xué)形式，本原性教學(xué)意味著教學(xué)要凸顯教學(xué)內(nèi)容的數(shù)學(xué)本質(zhì)。把師生的“眼光”都聚焦到對所教和所學(xué)內(nèi)容的數(shù)學(xué)本質(zhì)的探詢、理解和創(chuàng)造上來，而把對技能、技巧的訓(xùn)練和對經(jīng)驗(yàn)、情景的設(shè)計(jì)等視為其必要的“背景”，讓課堂充滿數(shù)學(xué)的“本味”。

作為一種教學(xué)設(shè)計(jì)的理念，本原性教學(xué)意味著教學(xué)應(yīng)扎根于學(xué)生的常識和經(jīng)驗(yàn)。關(guān)注其最原初、樸素的想法和真實(shí)的思維狀態(tài)，讓學(xué)生經(jīng)歷數(shù)學(xué)知識“再創(chuàng)造”的過程，不斷提升學(xué)生數(shù)學(xué)理解的水平，發(fā)展數(shù)學(xué)核心素養(yǎng)。

作為一種動態(tài)的思考教學(xué)的方式，本原性教學(xué)意味著要重塑教師的教育哲學(xué)。運(yùn)用哲學(xué)中對“本原”進(jìn)行連續(xù)不斷地追問和探詢的方式思考數(shù)學(xué)及其教學(xué)，讓師生共同體會到教學(xué)主題的數(shù)學(xué)本質(zhì)、原初觀念和核心思想，形成批判的意識和獨(dú)立思考的精神。

總之，本原性教學(xué)意味回歸“本原”，追問教學(xué)的本質(zhì)。這不僅是對數(shù)學(xué)教學(xué)現(xiàn)實(shí)的一種糾偏，更是對學(xué)科教學(xué)深層的本質(zhì)性的一種追尋。

二、數(shù)學(xué)“本原性教學(xué)”的實(shí)踐建構(gòu)

理念是一種莊嚴(yán)的理想，一種在經(jīng)驗(yàn)中無法遇見的完美性的概念。理念只有在具體的實(shí)踐中才能體現(xiàn)價(jià)值。作為追尋教學(xué)本質(zhì)中一種完美設(shè)想，本原性教學(xué)如何在具體的課堂實(shí)踐中落地生根，真正成為一種行之有效，并能夠引導(dǎo)課堂教學(xué)的核心觀念。下面結(jié)合教學(xué)實(shí)踐談一些粗淺的做法。

（一）立足數(shù)學(xué)視野，分析教學(xué)內(nèi)容

數(shù)學(xué)課中“數(shù)學(xué)味”流失的一種重要原因，就是教師缺失清晰的從數(shù)學(xué)角度考量教學(xué)的意識與視野！數(shù)學(xué)知識的教學(xué)，不僅僅是單一的、靜態(tài)的符號形式，更是數(shù)學(xué)思想方法、語言、文化的整體的、動態(tài)的綜合體現(xiàn)，學(xué)生數(shù)學(xué)素養(yǎng)的提升，必須在經(jīng)歷數(shù)學(xué)知識的探索過程中，感悟知識，形成技能，體驗(yàn)思想方法，獲得積極的情感體驗(yàn)。因此，教學(xué)分析不能僅僅限于教學(xué)方法的層面，還需要揭示數(shù)學(xué)本質(zhì)，從數(shù)學(xué)內(nèi)容上進(jìn)行提升！有效的教學(xué)依賴于教師對數(shù)學(xué)本質(zhì)的“深度理解”。

1.探詢教學(xué)內(nèi)容的本真意義

課改以來，教材編寫有一個(gè)顯著的特點(diǎn)，就是調(diào)強(qiáng)“數(shù)學(xué)生活化”，借助“生活原型”幫助學(xué)生理解“數(shù)學(xué)概念”，應(yīng)該說這個(gè)基本出發(fā)點(diǎn)是好的。但是，如果教師不能清醒地認(rèn)識到，學(xué)生在日常生活中自由生成的“純經(jīng)驗(yàn)”型的數(shù)學(xué)信息與真正意義上的“數(shù)學(xué)概念”之間的本質(zhì)區(qū)別，而只是一味停留在“情境”的層面展開教學(xué)，那么數(shù)學(xué)內(nèi)涵的流失將成為一種必然！

以“三角形的高”教學(xué)為例，什么是三角形的高？三角形的“高”與日常生活中的“高”的內(nèi)涵是一回事嗎？教材中從“人字梁”模型引入對學(xué)生理解三角形的高有沒有負(fù)面的干擾？事實(shí)上，三角形的高更應(yīng)該是數(shù)學(xué)上量化三角形的一個(gè)“參數(shù)”，跟長方形中的“長”和“寬”是類似的概念，而生活中的“高”多是豎直方向上物體的高度。清楚地認(rèn)識這一點(diǎn)，教學(xué)中顯然就不應(yīng)過分糾結(jié)是用“人字梁”這樣的素材，還是創(chuàng)設(shè)“小松鼠把三角形的蛋糕推進(jìn)樹洞”的情境，而應(yīng)該讓學(xué)生真切感受到“高”引入的數(shù)學(xué)價(jià)值，是數(shù)學(xué)中量化地研究圖形的需要。

對教學(xué)內(nèi)容中數(shù)學(xué)本質(zhì)的探詢，意味著教師要追問“生活數(shù)學(xué)”與“學(xué)校數(shù)學(xué)”的分野，從學(xué)科上對教學(xué)內(nèi)容的本質(zhì)有一個(gè)整體認(rèn)識和定位，構(gòu)建 “數(shù)學(xué)教學(xué)內(nèi)容知識（MPCK）”體系，形成自己對數(shù)學(xué)教學(xué)目的的統(tǒng)領(lǐng)性觀念。

2.把脈教學(xué)內(nèi)容的思想軌跡

依托教材分析教學(xué)內(nèi)容，有兩條“主線”值得我們深思。一條是數(shù)學(xué)知識體系的“明線”，它明明白白呈現(xiàn)在教材的例題中；另一條是隱含在知識體系中的思想方法——“暗線”。在“有形”的數(shù)學(xué)知識中蘊(yùn)含著“無形”的思想方法，需要我們透過具體的知識內(nèi)容，把脈教學(xué)整體的思想軌跡。

以“用數(shù)對確定位置”教學(xué)為例，有教師認(rèn)為：學(xué)生在考試?yán)铩靶小焙汀傲小比菀壮鲥e，因此在教學(xué)中想方設(shè)法進(jìn)行強(qiáng)調(diào)，讓學(xué)生反復(fù)操練以期取得良好效果。然而細(xì)細(xì)想來，“先列后行”真有那么重要，值得如此大費(fèi)周張嗎？事實(shí)上，透過“用數(shù)對確定位置”的知識表層，“一一對應(yīng)”的思想赫然在目！一個(gè)數(shù)對只能表示平面上一個(gè)點(diǎn)的位置，一個(gè)點(diǎn)只要也只能有唯一的數(shù)對表示。再進(jìn)一步思考，什么時(shí)候，我們只用一個(gè)數(shù)字，就能確定一個(gè)點(diǎn)位置？如果要確定魔方上一個(gè)小方塊的位置，用兩個(gè)數(shù)組成數(shù)對還行嗎？數(shù)學(xué)味的核心自然是數(shù)學(xué)，但絕對不是純粹的數(shù)學(xué)知識與技能，而是富有文化色彩的帶有鮮明數(shù)學(xué)特性的整體感。誠如教育家米山國藏所言：“作為知識的數(shù)學(xué)出校門不到兩年就忘了，唯有深深銘記在頭腦中的數(shù)學(xué)的精神、數(shù)學(xué)的思想、研究的方法和著眼點(diǎn)等，這些隨時(shí)隨地地發(fā)生作用，使人終身受益。”

3.對接教學(xué)內(nèi)容的思維方式

數(shù)學(xué)學(xué)習(xí)中每一個(gè)新的領(lǐng)域，都意味著一種新的思維方式。因此，教學(xué)不僅是建構(gòu)知識發(fā)展能力，更重要的是讓學(xué)生實(shí)現(xiàn)思維方式的轉(zhuǎn)變，實(shí)現(xiàn)由知識教學(xué)向智慧教學(xué)的跨越。波利亞指出：“只有理解人類如何獲得某些事實(shí)或概念的知識，我們才能對人類的孩子應(yīng)該如何獲得這樣的知識作出更好的判斷。”數(shù)學(xué)史對教學(xué)的借鑒意義，一個(gè)重要的方面就是對知識背后的思維歷程的理解和把握。

以“用字母表示數(shù)”的教學(xué)為例，教材（蘇教版）的例題是這樣呈現(xiàn)的：擺1個(gè)三角形用3根小棒，擺2個(gè)三角形用6根小棒，擺3個(gè)三角形、4個(gè)三角形呢？擺n個(gè)三角形呢？用字母表示是“n×3”。教學(xué)時(shí)，如果只是按照這樣的順序展開，課堂無疑是“順暢”的，但這里的“順暢”只是假象，因?yàn)榻虒W(xué)沒有觸及所教內(nèi)容的根本。那么問題出在哪里呢？其實(shí)“用字母表示數(shù)”的教學(xué)本質(zhì)在于學(xué)生思維方式的轉(zhuǎn)變，即從學(xué)生熟悉的算術(shù)思維向代數(shù)思維的轉(zhuǎn)換。顯然，這樣的轉(zhuǎn)換對學(xué)生來說并不是一件容易的事件，這也是造成學(xué)生填寫“青蛙歌”時(shí)教學(xué)尷尬的重要原因。為此，教學(xué)的重構(gòu)意味著讓學(xué)生感受到“n×3”不僅是一個(gè)算式，也能表示一個(gè)結(jié)果，并通過不斷由“過程”到“對象”的“凝聚”的過程中，讓學(xué)生體會到用字母表示數(shù)的本質(zhì)。

（二）站在兒童立場，構(gòu)建整體框架

小學(xué)數(shù)學(xué)的本質(zhì)是“兒童數(shù)學(xué)”。兒童學(xué)習(xí)數(shù)學(xué)一直以來都有其自身的方式，這是由兒童的生理和心理的特征決定的。教學(xué)中，如果片面凸顯數(shù)學(xué)之于教學(xué)的意義，一味地追求教學(xué)的深度，對于兒童來說，無疑是一場學(xué)習(xí)的災(zāi)難。弗賴登塔爾認(rèn)為：“學(xué)習(xí)數(shù)學(xué)的唯一正確的方法是實(shí)行‘再創(chuàng)造，也就是由學(xué)生本人把要學(xué)的東西，自己去發(fā)現(xiàn)或創(chuàng)造出來。”由此，真正意義上的教學(xué)是“數(shù)學(xué)味”與“兒童性”之間的一種平衡，是教學(xué)整體框架下兒童的內(nèi)在生長與自我完善。

1.從兒童的經(jīng)驗(yàn)出發(fā)

數(shù)學(xué)知識不僅包括被整個(gè)數(shù)學(xué)共同體所認(rèn)同的“客觀性知識”（科學(xué)形態(tài)的表征），還包括從屬于學(xué)生自己的“主觀性知識”（個(gè)體認(rèn)識的表征），即帶有鮮明個(gè)體認(rèn)知特征的“數(shù)學(xué)經(jīng)驗(yàn)”。學(xué)生的數(shù)學(xué)經(jīng)驗(yàn)反映了其對數(shù)學(xué)的真實(shí)理解。站在兒童立場，意味著數(shù)學(xué)教學(xué)應(yīng)當(dāng)植根于兒童經(jīng)驗(yàn)，呈現(xiàn)兒童經(jīng)驗(yàn)，發(fā)展兒童經(jīng)驗(yàn)。

在“折線統(tǒng)計(jì)圖”的教學(xué)中，我首先呈現(xiàn)條形統(tǒng)計(jì)圖并進(jìn)行分析，激活學(xué)生已有的數(shù)學(xué)經(jīng)驗(yàn)；然后引導(dǎo)學(xué)生從整體上觀察條形統(tǒng)計(jì)圖，并用手比畫氣溫的變化趨勢，同步畫出軌跡，把條形的頂端簡化為一個(gè)點(diǎn)，自然引入折線統(tǒng)計(jì)圖；在此基礎(chǔ)上引導(dǎo)學(xué)生比較兩者的異同，突出折線統(tǒng)計(jì)圖的特點(diǎn)。這樣的教學(xué)利用學(xué)生已有的數(shù)學(xué)經(jīng)驗(yàn)，使學(xué)生對折線統(tǒng)計(jì)圖的特點(diǎn)理解更加深入。

2.向數(shù)學(xué)的本質(zhì)邁進(jìn)

一味迷信“經(jīng)驗(yàn)”，過度向兒童的興趣妥協(xié)，會讓教學(xué)迷失方向！數(shù)學(xué)學(xué)習(xí)是讓學(xué)生經(jīng)歷“數(shù)學(xué)化”的過程，這其中既包括橫向數(shù)學(xué)化，也包括縱向數(shù)學(xué)化。橫向數(shù)學(xué)化是“把生活世界引向符號世界”，而在“符號世界里，符號的生成、重塑和被使用”，則是縱向數(shù)學(xué)化。

以“復(fù)式統(tǒng)計(jì)表”教學(xué)為例，從兒童的經(jīng)驗(yàn)出發(fā)，創(chuàng)設(shè)真實(shí)的問題情境，引導(dǎo)兒童體會單式統(tǒng)計(jì)表的局限性是教學(xué)的必然之意。然而，如果接下來還是按教材的設(shè)計(jì)呈現(xiàn)復(fù)式統(tǒng)計(jì)表，讓學(xué)生填寫數(shù)據(jù)的話，教學(xué)便失去了應(yīng)有的味道！換一種思路，讓學(xué)生在親身經(jīng)歷“合并”到“優(yōu)化”，體會復(fù)式統(tǒng)計(jì)表的創(chuàng)生過程，學(xué)生對復(fù)式統(tǒng)計(jì)表的結(jié)構(gòu)理解，對復(fù)式統(tǒng)計(jì)表獨(dú)特的價(jià)值理解會不會更加的深刻？其實(shí)兒童與其說是“學(xué)習(xí)數(shù)學(xué)”，毋寧說是兒童經(jīng)驗(yàn)的“數(shù)學(xué)化”。

（三）回到教學(xué)場域，把握關(guān)鍵性事件

學(xué)習(xí)是一種內(nèi)部過程，但它受外部的刺激或事件的影響。我們把對學(xué)生學(xué)習(xí)內(nèi)部進(jìn)程有重大影響的事件稱為教學(xué)中的“關(guān)鍵性事件”。把握教學(xué)中關(guān)鍵性事件有兩種不同的視野。第一種是我們常見的教學(xué)重點(diǎn)、難點(diǎn)分析。“重點(diǎn)”針對的是教學(xué)內(nèi)容，即什么是學(xué)生必須掌握的內(nèi)容要點(diǎn)，教師要把教學(xué)重心放在哪里，反映的是學(xué)科課程論。“難點(diǎn)”主要是針對學(xué)生的學(xué)習(xí)過程而言，即學(xué)生可能存在的認(rèn)知困難，反映的是學(xué)科學(xué)習(xí)論。第二種則來自對教學(xué)互動過程中“有意義事件”的辨別。其實(shí)，事件本身沒有關(guān)鍵與非關(guān)鍵之分，重要的是教師對所發(fā)生的事件的判斷和理解。

1.生成教學(xué)的“核心問題”

教學(xué)不能總是“在木板最薄弱的地方釘無數(shù)個(gè)釘，卻在木板最堅(jiān)固的地方無所為”。現(xiàn)實(shí)的課堂中“教師教得有模有樣，學(xué)生學(xué)得糊里糊涂”一個(gè)最根本的原因就是“核心問題”的缺失！用一句詩來說就是“你教或者不教，難點(diǎn)就在哪兒，不增不減！”教學(xué)的關(guān)鍵在于“學(xué)習(xí)共同體”的建立，而這主要取決于“核心問題”的生成，只有真正進(jìn)入師生視域交集中的問題才能成為教學(xué)的“核心問題”。

2.重塑教學(xué)的“對話品格”

教學(xué)的本質(zhì)是思維對話。“對話不是單純的言語應(yīng)答，而是各種價(jià)值相等、意義平等的意識主體相互作用的一種形式。”英國思想家戴維·伯姆認(rèn)為，“對話仿佛是一種流淌于人與人之間的意義溪流，它使所有對話者都能夠參與和分享這一意義之溪，并因此能夠在群體中萌生新的理解和共識。”

【教學(xué)片段】折線統(tǒng)計(jì)圖

師（故意設(shè)疑）：現(xiàn)在大家都會看折線統(tǒng)計(jì)圖了嗎？什么樣的折線統(tǒng)計(jì)圖都能看懂嗎？

生：能。

師：那我們來看一看這張統(tǒng)計(jì)圖。

生（驚奇）：這是什么統(tǒng)計(jì)圖啊？

師：不是說能看懂嗎？怎么都不說了呢？

生1：這個(gè)統(tǒng)計(jì)圖沒有標(biāo)題，也沒有數(shù)據(jù)，我們怎么知道統(tǒng)計(jì)的是什么呀？

師：是啊！沒有標(biāo)題和數(shù)據(jù)，確實(shí)不知道統(tǒng)計(jì)的是什么。但我們可以來猜一猜！有三個(gè)同學(xué)猜測的結(jié)果是這樣的。

課件出示：A同學(xué)：蘇州市1～5月份的平均氣溫；

B同學(xué)：某同學(xué)跳繩后5分鐘的心跳次數(shù)；

C同學(xué)：某同學(xué)最近5次數(shù)學(xué)測試的成績。

師：你覺得哪個(gè)同學(xué)的猜測比較合理呢？

生2：我認(rèn)為B同學(xué)的比較合理。我們跳繩后開始心跳得比較快，后來就平靜了下來，所以5分鐘心跳的次數(shù)比較合理。

師：為什么不選A呢？

生2：蘇州市1～5月份的平均氣溫應(yīng)該是越來越高。折線應(yīng)該上升而不應(yīng)該是下降，所以A不可能。

生3：我們認(rèn)為C也有可能。

師：為什么？如果是C的話，你覺得這個(gè)同學(xué)的成績怎么樣？

生：不好，很差！

師：那如果是你的成績，你覺得折線應(yīng)該是什么樣子的呢？

（學(xué)生用手從低到高比劃折線的變化趨勢）

師（微笑）：是這樣嗎？想好了嗎？

生4：不對，不對！，我認(rèn)為應(yīng)該是這樣——（用手沿水平方向比劃）

師：什么意思？

生4：每次都是100分。（眾生大笑）

上述案例中，圍繞“這幅統(tǒng)計(jì)圖統(tǒng)計(jì)的是什么呢？”“你覺得哪個(gè)同學(xué)的猜測比較合理？”“如果是你的成績，你覺得折線應(yīng)該是什么樣的呢？”等問題，教師一步一步地將學(xué)生的思考引向深入，在尋找與折線統(tǒng)計(jì)圖相吻合的數(shù)據(jù)的過程中，深化學(xué)生對折線與數(shù)據(jù)之間對應(yīng)關(guān)系的理解，同時(shí)，不完整的統(tǒng)計(jì)圖將學(xué)生思維進(jìn)一步聚焦到“折線”上來。對“折線”特征的分析過程，其實(shí)就是對“折線”中蘊(yùn)涵的豐富信息的解讀過程，而這恰恰是學(xué)生數(shù)據(jù)分析觀念的核心所在。

課堂對話永遠(yuǎn)充滿著精彩的未知與可能，教學(xué)中的對話不是漫無目的的閑談，而是教師、學(xué)生、數(shù)學(xué)之間“視界融合”的過程，是意義不斷創(chuàng)造與生成的過程。重塑教學(xué)的對話品性，意味著對話要圍繞教學(xué)的核心問題展開，并推進(jìn)教學(xué)活動不斷成為學(xué)生發(fā)展中的關(guān)鍵性事件。

“本原”原本是哲學(xué)研究中的一個(gè)冷峻字眼，但它同時(shí)把我們帶入了一個(gè)追求本質(zhì)、回歸原初的境界。數(shù)學(xué)教學(xué)不應(yīng)該是日復(fù)一日地重復(fù)某種固定的“模式”，因?yàn)榻虒W(xué)經(jīng)驗(yàn)的嫻熟并不一定代表教學(xué)的進(jìn)步。追問實(shí)踐、澄清理念、重寫自己的教育哲學(xué)，或許，對于“本原性教學(xué)”的追求只是個(gè)美好愿望，但誰又能不懷揣著愿望前行呢？

（責(zé)編 金 鈴）