小學數學教學中如何培養學生的創新能力

黃勝亮

摘 要：針對當前對創新教育的重視和迫切需求，結合本人多年的教學經驗，總結了培養創新能力的幾點見解：學習興趣是培養創新能力的前提，合理的問題情境是培養創新能力的契機，加強實踐操作是培養創新能力的重要途徑，促進求異思維的發展是培養創新能力的關鍵。并結合具體的案例進行闡述。

關鍵詞：小學數學；創新能力；實踐操作；求異思維

一、實踐操作是培養創新能力的有效途徑

《數學課程標準》中強調指出：動手實踐、自主探索與合作交流是學生學習數學的重要方式，學生學習活動應當是一個生動活潑的、主動的和富有個性的過程。教學時，教師要放手讓學生充分利用身邊的工具和學具，參與操作，培養學生創新能力。數學上的實踐操作主要有“作圖實踐”，“實物操作”，“實景運用”三類。”

1.作圖實踐

在小學數學中，作圖實踐最常見的就是作線段圖和幾何圖形（三角形，梯形，平行四邊形，圓，長方體，立方體），是學生必備的學習技能。它往往用在解題中，起到化難為易，化抽象為具體，化復雜為簡潔作用，為開啟學生的思路，迸發創新火花提供了很大的幫助。

案例：

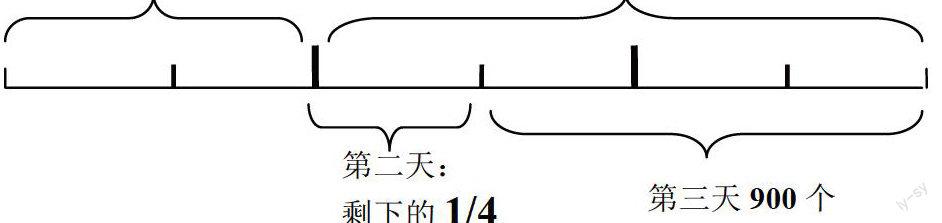
工廠加工一批零件，第一天加工了這批零件的1/3，第二天又加工了剩下的1/4，第三天只需要加工900個就可以完成所有的任務，請問這批零件一共有多少個？

【部分學生解法】

（1）900÷（1-1/4） ÷（1-1/3） =1800（個）

【這種方法雖然正確，但是稍顯復雜，基礎差的同學比較難理解。】

（2）900÷（1-1/3-1/4）=2160（個）

【這種方法顯然是錯誤的，把單位“1”的量錯誤地認為是零件總數。】

【作圖研究，得出新方法】

通過線段圖，學生才恍然大悟，很快就發現其中訣竅，得出了：

總數： ？——6份 第三天： 900——3份（剛好一半）

列式： 900÷3×6=1800（個）或900×2=1800（個）

縱觀整個解題過程，我們要感謝線段圖的作用，它讓原本抽象的題目變得很直觀，讓深藏在其中的奧秘一覽無遺地出現在學生的眼皮底下，從而為學生開啟了創新的契機。

2.實物操作

實物操作，就是讓學生借助具體的實物，通過動手操作，觀察，比較等方式，發現數學問題，并創造性地加以解決，特別對于一些抽象概念、規律與方法是極其有利，它能使抽象的問題具體化和直觀化，讓學生更容易理解。通過實踐活動，培養了學生的思維能力，創造能力。同時，操作實踐也是破除思維定勢的重要途徑之一。

案例：

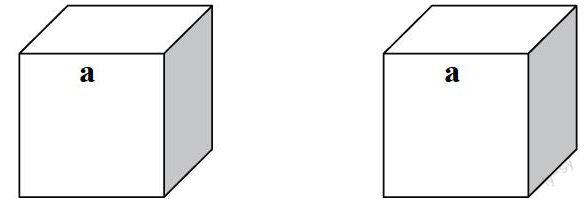
在教學有關“立體圖形拼，截問題”中，老師出示：“把兩個棱長都是a厘米的正方體拼成一個長方體，這個長方體的表面積是多少平方厘米？”

【錯誤解法】6a2+6a2=126a2

【動手操作，取得實效】

這時老師讓學生拿出兩個正方體拼一拼，并觀察物體表面前后有什么變化？經過操作研究，有些同學才恍然大悟，拼成后的長方體比兩個立方體少了兩個正方形的面，得出了長方體表面積是（12—2）a2，同時“截”的問題，也就能迎刃而解了。

【延伸拓展，尋求規律】

在此基礎上，趁熱打鐵，如果有3，4，……N個立方體拼在一起，表面積有什么變化？雖然學生還沒有能力得出有關長方體表面積和N之間的表達式，但是他們都知道，每增加一個立方體的拼接，就會少了兩個面。

三、促進求異思維的發展是培養創新能力的關鍵

古人云：“學貴有疑，學則須疑。” 在創造性思維活動中，求異思維和求同思維密不可分，但求異思維參與相對多一些，因此訓練求異思維，顯得尤為重要。促進求異思維的方法和途徑，首先體現在各科教學活動中，作為教師要做到“教學有法，但無定法”。

1.完全錯誤版的求異思維。這種求異思維，在課堂上很常見，部分同學考慮問題出現偏差而導致思想方法出現錯誤，往往得到“吃力不討好”的后果。對于這樣的求異思維產生，教師首先應該尊重它，在評價過程中應該肯定它的積極的一面，繼而分析它產生錯誤的原因，進行修正，最后總結經驗，讓全體同學都得到一次錯誤的教訓。

2.部分正確版的求異思維。部分正確版的求異思維，往往表現為解決問題的思想方法運用恰當合理，甚至具有一定優越性，但是在解決的過程中，出現了知識運用上的錯誤，從而造成了思維模糊，不得其解。這樣的求異產生，具有很深的研究價值，通過研究其思想方法，分析錯誤根源，繼而完善這種解決方法，這一系列的過程，學生既吸收了新的思想方法，鞏固了知識，又培養了思維活動能力和創新能力。

案例：在一節練習課上，有這樣一道題：在一幅比例尺是1：5000的地圖上，量得正方形的邊長是4厘米，求正方形的實際面積。

【一位同學的解法】 4×4=16 cm2=0.0016 m2，【圖上面積】

0.0016×5000=8 m2 【實際面積】

該同學解法似乎每一步都有道理，但是問題出在哪里呢？

【分析原因】

該同學的思想方法完全正確，但是在知識運用的過程中，忽視了面積比和長度比的區別。比例尺是正方形的邊長之比，根據正方形面積公式，面積之比應該是1：50002，所以實際面積應該是圖上面積的50002 倍，也就造成成了兩個結果（4000 m2和8 m2）剛好是5000倍的關系。

【正確解法】4×4=16 cm2=0.0016 m2，【圖上面積】

0.0016×50002=40000 m2 【實際面積】

【得出結論】面積之比是比例尺的平方比

之后趁熱打鐵，還得出了長度比，面積比，體積比之間的關系。

這個求異思維的產生，既讓學生掌握了新的思想方法，又讓原有的知識得到“升華”，真正實現了創新。

參考文獻：

[1]《小學數學教育》 2008年第6期.

[2]《做最好的老師》 李鎮西著.

[3]《知識結構與創新思維》 胡列著.

[4]《創新能力和職業道德知識讀本》國家行政學院出版社.