中職數學三角函數誘導公式的教學探討

任國利

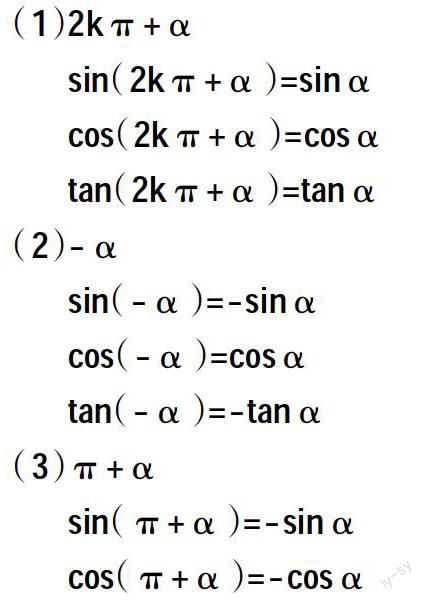
摘要：目前我國正在大力地發展職業教育，數學對于培養學生的理性思維、分析推理能力有著不可代替的重要作用.三角函數是數學的基礎知識，在數學的學習中都有著重要的不容忽視的核心地位與重要作用.中職數學三角函數誘導公式這節內容，在三角函數部分具有非常重要的地位.學生能夠掌握并正確運用誘導公式，對解決三角函數有關問題會起到事半功倍的作用.筆者就多年來的教學實踐，結合中職學生的具體實際，談一談誘導公式教與學的一些做法，以期為其他同行教師提供一些參考.

關鍵詞：中職數學；三角函數；誘導公式；教學探討

中圖分類號：G712 文獻標志碼：A 文章編號：1674-9324（2016）14-0283-02

目前我國正在大力地發展職業教育，職業教育的價值不僅表現為經濟發展、社會和諧作做出了貢獻，而且在促進社會就業、個人發展方面做出了貢獻.數學對于培養學生的理性思維、分析推理能力有著不可代替的重要作用，數學是學習專業技能知識的重要工具.三角函數是數學的基礎知識，也可以說是幾乎所有高科技的基礎，它是基本初等函數中的一種，在數學的學習中都有著重要的不容忽視的核心地位與重要作用.

中職數學三角函數誘導公式這節內容，在三角函數部分具有非常重要的地位.學生能夠掌握并正確運用誘導公式，對解決三角函數有關問題會起到事半功倍的作用.三角函數誘導公式是中職數學三角函數部分的重要公式，然而三角函數誘導公式多而復雜，利用傳統誘導公式求解相應的三角函數，步驟多且難以理解.如何解決這一難題？筆者在多年的教學中總結教學經驗，改變傳統教學模式，將三角函數誘導公式進行拓展，化難為易，以適應中職生的學習需求.下面筆者就多年來的教學實踐，結合中職學生的具體實際，談一談誘導公式教與學的一些做法，以期為其他同行教師提供一些參考.

中職數學誘導公式共有2kπ+α，-α（或2π-α），π+α及π-α四套公式.利用公式的目的就是要把求任意角的三角函數值轉化為求銳角的三角函數值.以往學生在學習本節內容時最大的困惑是記不住公式和不會運用公式.現就以上問題和大家一起探討我在上課時不太成熟的解決問題方法.

一、推導公式

中職教材公式的推導方法學生不易理解，即使聽懂了，學生也記不住.我在教學誘導公式時，先引導學生觀察上述四套公式，學生會發現幾套公式中，都與2π或π有關，化簡后三角函數名稱都不變，符號有的改變，有的沒變.然后引導學生總結出利用誘導公式求三角函數值“三角函數名稱不變，符號看象限”的口訣.這里如何確定角的象限至關重要.例如：π+α這套公式，先設α為銳角，則π+α為第三象限的角，第三象限角的正弦值為負，故sin（π+α）=-sinα；同理，第三象限角的余弦為負，故cos（π+α）=-cosα；第三象限角的正切為正，故tan（π+α）=tanα.這樣學生只要記住不同象限角的三角函數值的正負情況，自己就能輕松推導出公式.不同象限角的各種三角函數值的正負口訣是：“一全正、二正弦、三為切、四正弦.”

學生推導完公式之后，讓他們和教材公式對照比較，發現完全正確，他們一定會有一種成就感.這時教師不失時機地強調，當角α為任意角時，上述公式照樣適用.通過以上的方法教與學，學生能夠非常順暢地掌握公式.即使課后學生忘記了，自己也能輕易地推導出來.這樣，在課堂上就能節省大量時間.原來需要四節課才能講完的內容，兩節課就能講完，并且效果還好.這樣也極大地增強了學生學習數學的積極性.

二、運用公式

我們在教學過程中教給學生掌握公式固然重要，但讓學生會正確地使用公式更重要.不會使用公式從理論上說等于零.就像士兵一樣，擁有了先進的，強大的武器裝備，但不了解其性能，不會使用它，一點用都沒用.我們在教學中遇到問題最多的是：學生經常問老師這些公式怎么用.所以教師教會學生如何正確使用公式至關重要.

三、課后思考

師者，所以傳道授業解惑也.授之魚不如授之以漁.教師不但要善于傳授知識，還要能夠幫助學生總結規律性的東西，并且運用規律解決實際問題.要正確引導學生善于觀察問題、分析問題，進而解決問題.我在講授三角函數誘導公式時，沒有利用單位圓和對稱的性質進行復雜的推導，那樣講對于職業學校基礎較差的學生來說太難了.而我通過三角函數誘導公式知識的教與學，是要讓學生學會一種數學思想，那就是不完全歸納法的具體運用.它和學習等差數列、等比數列通項公式一樣，根據等差數列和等比數列的定義，利用不完全歸納法非常自然地歸納出等差數列和等比數列的通項公式.我們推導三角函數誘導公式時，先設角α為銳角，利用不同象限角的三角函數值的符號，引導學生毫無費力地推導出每個公式，最后讓學生明白當角α為任意角時照樣適用.在這樣的數學思想指導下，學生就能自主輕松地推導公式，掌握公式，達到事半功倍的效果.從而突破了本節課的難點，為順利求出各種形式的角的三角函數值打下堅實的基礎.在求任意角三角函數值時，教師也要引導學生觀察，分析每一套公式的特點和使用的條件，讓學生做到有的放失，少走彎路，經過一段時間的訓練，很自然地學會利用哪個公式求值了.

總之，教師上好每一節課，不是簡單地傳授知識，而是要注重引導學生善于發現規律、總結規律.讓學生更好地運用知識解決實際問題，從而搞好我們的教學工作.這樣也能更好地發揮數學工具科的作用，更好地為專業課教學服務，提高學生的文化素質和專業技術素養.

參考文獻：

[1]趙衛國.高中數學公式與定理教學“五步曲”[J].中學數學研究，2011，（04）.

[2]覃桂燕.幾何畫板在三角函數教學中的應用[J].廣西教育學院學報，2011，（01）.

[3]許欽彪.任意角三角函數的教學反思[J].數學教學研究，2008，（02）.

[4]陳潔.對信息技術與數學教學整合的思考[J].中學數學月刊，2010，（05）.

[5]劉揚.中職學生的三角函數教學探討[J].數學學習與研究，2010，（05）.

[6]劉艷.基于情境認知理論的中職數學教學設計初探[J].湖北廣播電視大學學報，2008，（04）.

[7]雷彬.對教育信息化發展現狀的思考及建議[J].中國教育信息化，2008，（07）.

[8]阮佩文.專業背景下中職數學的應用性教學[J].職業教育研究，2008，（01）.

[9]岑煥云.中職汽修專業數學課程開發初探[J].職教論壇，2007，（18）.

[10]李翔.對中職新大綱“三角函數”的認識與教學建議[J].科技創新導報，2010，（30）.