在課堂教學中如何對接學生的已有經驗
胡明喜
【關鍵詞】學生經驗 生態課堂 小學數學 課堂教學
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2016)10A-0060-02
在小學數學教學過程中,教師應幫助學生從已有經驗向學習經驗跨越,最終實現經驗的對接和提升,構建教師和學生、學生和思維的自然生態系統。然而,在實際教學中往往會出現學生經驗與教學經驗的割裂,導致教師的教學路徑與學生經驗不吻合,這種教與學的不對稱,嚴重破壞了數學課堂的生態體系,不利于提高學生的數學能力。如何對接學生經驗,實現和諧自然的課堂生態呢?筆者認為,教師要基于學生的原有經驗和再生經驗,從活動經驗、生活經驗、操作經驗、實踐經驗四個層次入手,以整體架構的視野深入剖析,進行有效地對接、改造和重組。
一、對接活動經驗,實現課堂生態
所謂活動經驗,指的是學生在數學活動中獲得的低層次經驗。在小學數學教學中,教師要找準學生的活動經驗,進行有效對接,打通課堂教學的通道,實現和諧自然的課堂生態。
在教學蘇教版數學三年級下冊《長方形和正方形的面積》時,學生通過學習測量單位,已經積累了目測、用正方形拼擺疊測、不斷剪拼疊測的活動經驗,但在“教”的過程中,則需要學生具有利用第三方進行面積測量的數學經驗。基于此,為了讓學生實現思維活動經驗和所需經驗的對接,修復教學斷層,筆者從學生活動經驗入手,設計了以下教學引導。
筆者讓學生用目測法比較課桌桌面與數學課本封面的大小之后,引導學生估測一下大概有幾本書能鋪滿課桌面。由此,學生積累了借助課本鋪一鋪的測量經驗;接著,筆者在黑板上畫出一個長方形,讓學生比較課桌面與這個長方形的大小。學生發現這兩個面的大小差不多,無法用目測得出結論,但也不能將課桌面和這個長方形進行疊測,怎么比較面積大小呢?學生根據剛剛積累的“鋪一鋪”的測量經驗,提出課桌面相當于8個數學課本的封面,只要量出這個長方形相當于幾個數學課本的封面就可以了。通過引導,學生領悟到要借助第三方來進行大小比較,由此實現了活動經驗和所需經驗的斷層修復,激活了學生運用第三方進行面積測量的經驗。
本環節教師立足學生已有的活動經驗,借助數學課本鋪桌面的數學活動,啟動經驗序列,讓學生有效地把握面積測量的本質,幫助學生完成經驗的提升,促進了教學斷層的修復,實現了數學課堂的和諧生態。
二、對接生活經驗,實現課堂生態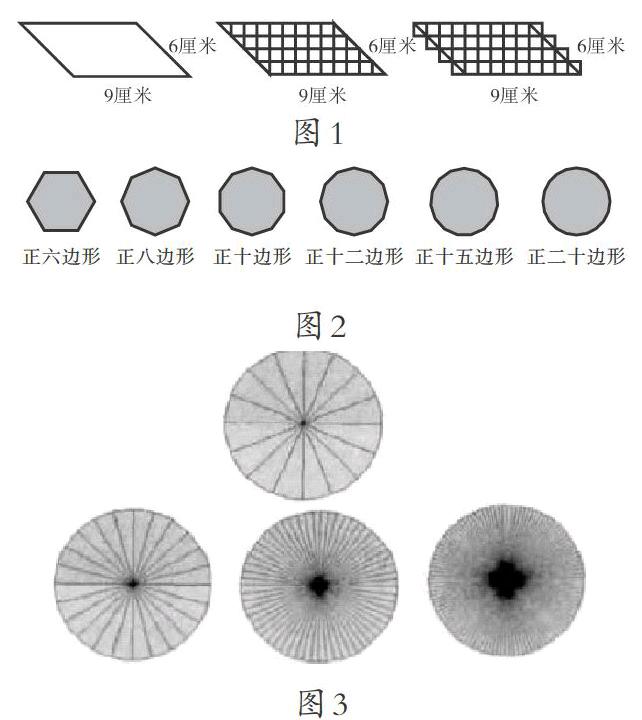
小學生都積累了一定的生活經驗,教師要結合學生的實際情況,將生活經驗和教材內容有效對接,幫助學生深刻理解數學知識,豐富活動經驗。
在教學蘇教版數學五年級上冊《小數加減法》一課時,小數加減法的計算法則容易掌握,但計算法則中數位對齊的算理則是本課的教學難點。為了讓學生深入理解相同數位要對齊的算理,筆者列舉了生活中的實例,讓學生進行思考:小明原來有5元4角,后來媽媽又給了(或拿走了)3元5角,他現在還有多少錢?你怎么計算這道題?學生認為,可以先將5元和3元相加減,再將4角和5角相加減。此時筆者繼續引導:你發現了計算的規律是什么?學生根據這一生活經驗,體會到要將相同的計量單位對齊。此時筆者追問:在小數加減法計算時,為什么相同數位要對齊?學生由此進行了深刻的思考,有了深入的理解。
以上教學,教師根據學生已有的生活經驗,有效對接到要學習的數學新知上面,不但豐富了學生的已有經驗,而且提升了學生的經驗積累,有效地增強了學生對新知識的理解。
三、對接操作經驗,實現課堂生態
在小學數學教學中,學生往往容易根據之前的操作形成經驗,因此,教師要善于發現學生的操作經驗,找準這種操作經驗與應用經驗之間的斷層進行有效對接,實現課堂生態。
在教學《平行四邊形面積的計算》一課時,學生根據長方形的面積計算公式長×寬,形成了操作經驗,猜想將平行四邊形轉化為長方形,因此面積為底邊和鄰邊相乘。在“教”的路徑中,學生需要的是剪拼轉化的應用經驗。為此,筆者立足學生的這一操作經驗,進行有效引導:當學生堅信平行四邊形的面積等于底邊乘鄰邊=9×6=54(平方厘米)時,筆者將格子圖展示出來(如圖1),學生由此認識到,可以通過面積測量的方法,將每行擺單位面積的個數×擺的行數,將平行四邊形的面積劃定在8×4和10×4之間。此時筆者再展開教學引導,讓學生利用格子圖探究平行四邊形的面積計算公式,從而深刻理解長方形面積和平行四邊形面積的差異,對平行四邊形的面積、底、高、鄰邊與長方形的面積、長、寬之間的聯系和區別有了初步的認知,實現了經驗對接和改造。
以上環節,教師立足學生的操作經驗,讓學生從錯誤中感悟問題所在,從錯順利過渡到對,從破順利過渡到立,從而將操作經驗有效提升至應用經驗的高度,實現了課堂生態。
四、對接概括性經驗,實現課堂生態
在小學數學教學中,學生在遇到一些類似的數學情境時,往往會按照舊模式解決問題,這種經驗就叫做概括性經驗。在蘇教版數學六年級上冊《圓的面積計算》教學中,近一半的學生會根據直線圖形(平行四邊形面積、三角形面積、梯形面積)中的割補、拼接的實踐性經驗,認為可以將圓轉化為平行四邊形。但由于圓是曲線圖形,而不是直線圖形,所以學生在轉化中陷入了困境。于是,如何將這一實踐性經驗應用在圓這個曲面圖形,成了課堂教學的重點。如何對接這一實踐性經驗,讓學生體會化曲為直和極限的數學思想,提高學生的數學經驗,實現數學課堂生態呢?筆者做了四個層次的引導,幫助學生積累相應的經驗。
其一,積累化曲為直的轉化經驗。通過操作,讓學生用線繞成圓再拉直,將正方形紙折成圓扇,感受并體會直線圖形轉化為曲線圖形。
其二,體驗圓始于方的極限思想。先從圓內接三角形入手進行直觀展現,引導學生想象正六邊形、正八邊形……(如圖2)學生發現,圓就是一個正無數邊形,有無數條邊,每個邊就是一個點。
其三,積累中心切割經驗。引導學生將正八邊形分割成八個一樣大的三角形,然后用底×高÷2×8求出面積。由此,學生認識到只要沿著N邊形中心點與頂點的連線,將其分割成N個一樣大的三角形就可以求出面積。
其四,根據實踐性經驗展開自主推導。大部分學生已經有了中心切割正多邊形的實踐經驗,此時筆者引導學生思考:圓如何分割成三角形?分割出來的三角形和圓的什么有關?通過直觀操作(如圖3),學生提出可以將圓平分成8個近似的三角形,三角形的底邊就是周長,高就是半徑,面積就是周長×半徑÷2×8,也就是周長×半徑÷2;還有學生提出可以將圓平均分成24個近似的三角形,圓的面積等于周長×半徑÷2.
以上教學,教師立足對接學生的實踐性經驗,設計了四個層次的經驗鋪墊,讓學生經過對化曲為直的轉化鋪墊,直觀感受到了極限和無窮分割,從而有效提升了實踐性經驗,感悟到其中蘊含的數學思想,并由此獲得圓面積推導所需的經驗。
總之,教師要善于在學生和教材之間把握平衡,不但要找到學生的已有經驗,還要把握和尋找學生已有經驗與教材所需經驗之間的斷層,并由此結合已有經驗,通過改造、重組、修復、提升,順利過渡并有效對接,這是每一個教師都亟待思考的課題,也是實現課堂生態的關鍵所在。筆者相信,把握學生經驗,有效對接已有經驗,就能夠打通教與學的通道,讓數學課堂實現自然的和諧生態。
(責編 林 劍)

