高效課堂從“頭”開始

劉洪志

摘 要：課堂教學(xué)導(dǎo)入的好壞直接影響一節(jié)課教學(xué)效果的好壞，因此，教師在設(shè)計(jì)課堂導(dǎo)入方式上要下功夫，多加思考。

關(guān)鍵詞：高中數(shù)學(xué)；課堂教學(xué)；引入方式

中圖分類號：G633.6文獻(xiàn)標(biāo)識碼：A 文章編號：1992-7711（2016）17-060-2

高中數(shù)學(xué)課堂的導(dǎo)入情境就是在新的教學(xué)內(nèi)容或教學(xué)活動(dòng)開始前，創(chuàng)設(shè)一定的教學(xué)情境，引導(dǎo)學(xué)生進(jìn)入學(xué)習(xí)狀態(tài)的教學(xué)行為。一堂課就像一首樂曲，教學(xué)的開始也就是課堂引入，就像樂曲的開始“起調(diào)”，我們知道好的開始能起到事半功倍的效果，若是課堂引入生動(dòng)形象、立意巧妙、引人入勝，定能撥動(dòng)學(xué)生的心弦，立疑激趣，促使學(xué)生的學(xué)習(xí)情緒高漲，自覺主動(dòng)地步入智力振奮狀態(tài)，充分調(diào)動(dòng)探求新知的積極性和自覺性，能夠把數(shù)學(xué)的冰冷的美麗變成同學(xué)火熱的思考，高效課堂就有了基本的保證。

南京師范大學(xué)涂榮豹先生在他的著作《新編數(shù)學(xué)教學(xué)論》中提出課堂引入遵循的五個(gè)原則，即目的性、針對性、激勵(lì)性、啟發(fā)性、探究性。我們沒有辦法保證每節(jié)課的引入都滿足五個(gè)原則，但是根據(jù)授課內(nèi)容的不同，我們的引入設(shè)計(jì)可以注重其中的一到兩條，從而提高學(xué)生的“入境”效率。本文選取五個(gè)教學(xué)引入情境的例子，希望能引發(fā)數(shù)學(xué)教師在自己的課堂設(shè)計(jì)上的思考。

一、談思想，論方法，增加引入目的性

案例1：蘇教版必修2第三章《立體幾何初步》中，“平面與平面的位置關(guān)系”第一課時(shí)的引入我是這樣設(shè)計(jì)的：同學(xué)們，上一節(jié)課我們已經(jīng)研究了直線與平面的位置關(guān)系，我們根據(jù)直線和平面的公共點(diǎn)的個(gè)數(shù)得出直線和平面可以相交、平行，線在面內(nèi)。下面請同學(xué)們觀察教室里的平面，說說他們有怎樣的位置關(guān)系？請你拿兩本書當(dāng)做兩個(gè)平面，擺一擺，看看他們有怎樣的位置關(guān)系？

本節(jié)課我們可以類比線面平行的研究方式來解決面面平行問題。類比思維的理論依據(jù)是事物之間具有相似性。從數(shù)學(xué)問題的發(fā)現(xiàn)或提出新命題的過程來看，大量是從具體問題或素材出發(fā)，經(jīng)過類比、聯(lián)想等途徑，形成命題（猜想）再加以確認(rèn)的。高中數(shù)學(xué)教材中屬性相似的內(nèi)容占有較大比例，集合的運(yùn)算與實(shí)數(shù)的運(yùn)算；指數(shù)函數(shù)與對數(shù)函數(shù)；等差數(shù)列與等比數(shù)列；四種二次曲線（圓、橢圓、拋物線、雙曲線）；空間幾何性質(zhì)與平面幾何性質(zhì)；三種多面體及四種旋轉(zhuǎn)體；向量與復(fù)數(shù)，排列與組合等等。因此，在教學(xué)過程中，可抓住其發(fā)生過程、內(nèi)涵、結(jié)構(gòu)、性質(zhì)以及解決問題的數(shù)學(xué)思想方法等方面的相似性來設(shè)計(jì)問題的引入，由此及彼，觸類旁通。這種引入方式能夠有效利用已有的知識基礎(chǔ)，讓新知識自然而然生長出來，更符合建構(gòu)主義教學(xué)觀。

二、刪繁瑣，去浮華，增加引入針對性

案例2：蘇教版數(shù)學(xué)必修1第二章《指數(shù)函數(shù)的概念》：

亞里士多德曾經(jīng)說過：“給我一個(gè)支點(diǎn)，我就能撬動(dòng)地球。”

劉老師說：“給我一張紙，帶你走進(jìn)奇妙的數(shù)學(xué)世界。”

問題1：一張白紙厚度為0.06mm，三中教學(xué)20米我要踩著這張紙上樓能不能做到？（學(xué)生有笑聲）

問題2：一張紙?zhí)×?，不夠高，我進(jìn)行下面的操作：

（1）對折一次，白紙有幾層？

（2）對折兩次，白紙有幾層？

（3）對折三次，白紙有幾層？

……

（4）對折十次，白紙有幾層？厚度有多少？

（5）對折40次，白紙有幾層？厚度有多少？

（6）對折x次，白紙有幾層？層數(shù)與折疊次數(shù)的關(guān)系式是什么？

其中問題（5）的結(jié)果相當(dāng)于繞地球赤道大約1.65圈?。ǖ厍虬霃?.37×103km）。

從一個(gè)熟悉的游戲出發(fā)，用“薄薄的紙”和大樓的高度這兩個(gè)強(qiáng)烈的反差來激發(fā)學(xué)生的學(xué)習(xí)熱情和探求欲望。本節(jié)課是在學(xué)習(xí)了函數(shù)的定義及其圖象、性質(zhì)，掌握了研究函數(shù)的一般思路，并將冪指數(shù)從整數(shù)擴(kuò)充到實(shí)數(shù)范圍之后，學(xué)習(xí)的第一個(gè)重要的基本初等函數(shù)。重點(diǎn)是y=2x（x∈N*）是不是函數(shù)？這個(gè)函數(shù)具有什么性質(zhì)？如何來研究這個(gè)函數(shù)的性質(zhì)？因?yàn)檎n題的研究方法和手段學(xué)生很容易遷移過來，因此在課的設(shè)計(jì)上力求簡潔，去掉過分繁瑣的實(shí)際背景，針對課程的重點(diǎn)，設(shè)計(jì)恰如其分情境引入，增加課堂教學(xué)的實(shí)效性。

三、抓時(shí)機(jī)，盯熱點(diǎn)，增加引入激勵(lì)性

案例3：蘇教版必修5第十三章《基本不等式》復(fù)習(xí)課，學(xué)習(xí)本節(jié)課時(shí)正值2014年巴西世界杯如火如荼，我了解到班里很多男生都在熬夜看球，于是就這樣設(shè)計(jì)了開始環(huán)節(jié)：足球比賽中，最狂熱激情的時(shí)刻莫過于進(jìn)球時(shí)刻。不少進(jìn)球都是匪夷所思的，任意球、角球，都是進(jìn)球的好時(shí)機(jī)。先不說射門者的技術(shù)，像羅納爾迪尼奧在2002年世界杯吊英格蘭門將希曼那一球，貝克漢姆那腳驚世駭俗的在中線右側(cè)的吊門，都是苦練多年練就的（此處視頻展示兩個(gè)進(jìn)球）。但只有技術(shù)，不會(huì)選擇射門的時(shí)機(jī)和地點(diǎn)一樣無法射出精妙的球。所以選擇射門的地點(diǎn)也是一個(gè)必須考慮的因素。在什么位置選擇射門才最有可能進(jìn)球？

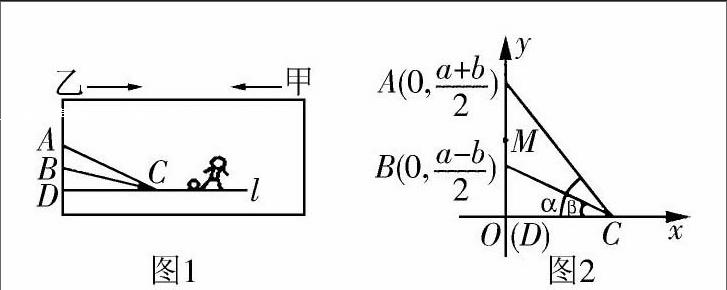
在足球比賽中，甲方邊鋒從乙方所守球門附近帶球過人，沿直線向前推進(jìn)。試問：邊鋒在何處射門的可命中角最大？如圖，足球比賽場地的寬為a米，球門寬為b米，在足球比賽中，甲方邊鋒從乙方球門附近帶球過人，沿直線l（貼近球場邊線）向前推進(jìn)，試問，該邊鋒在距離乙底線多遠(yuǎn)時(shí)起腳射門的命中角最大？（注：圖1中AB表示乙所守球門，AB所在直線為乙方底線，l表示甲方邊鋒前進(jìn)的直線）

數(shù)學(xué)來源于生活，反過來要指導(dǎo)生活！興趣是最好的老師，教師的課堂設(shè)計(jì)要能激發(fā)學(xué)生最原始的學(xué)習(xí)動(dòng)力。波利亞曾提出數(shù)學(xué)教與學(xué)的最佳動(dòng)機(jī)原則，如果學(xué)習(xí)者缺乏活動(dòng)的動(dòng)機(jī)，就不會(huì)有所行動(dòng)；相反，學(xué)習(xí)者能經(jīng)歷用已有的知識無法解決某些問題，感覺到有學(xué)新知識的必要性，必能激發(fā)其學(xué)習(xí)的熱情和探索的主動(dòng)性。當(dāng)然這就需要教師要了解學(xué)生，了解社會(huì)，不管是體育、文藝、政治、經(jīng)濟(jì)等等，把學(xué)生關(guān)注的人和事合理化處理，讓它能為教學(xué)服務(wù)，真正達(dá)到為我所用的地步，讓學(xué)生感受到數(shù)學(xué)不只在課本里，也在生活中。

四、道至簡，聲奪人，增加引入啟發(fā)性

案例4：在學(xué)習(xí)數(shù)學(xué)歸納法時(shí)，恰逢我在外地開會(huì)回來，我就以這個(gè)話題編一個(gè)新課引入：我們?nèi)繀⒓訒?huì)議的人員都住在某賓館的同一棟樓，報(bào)社記者預(yù)前往采訪，但不知道與會(huì)者的住處，就問賓館服務(wù)員。該服務(wù)員對記者說：“301住的是（參會(huì)人員）”然后又加了一句：“按房號，前一個(gè)住的是（參會(huì)人員），后一個(gè)也是（參會(huì)人員）?！睂W(xué)生頓了一下，馬上明白過來，我就把服務(wù)員的話和“數(shù)學(xué)歸納法”聯(lián)系了起來，教學(xué)活動(dòng)自然而然的開展起來。

創(chuàng)設(shè)引入情景，要能把復(fù)雜的道理簡明化、要先聲奪人，要能有意無意明示或暗示學(xué)生需要思考的問題解決方向和方法，要能促使學(xué)生積極參與課堂教學(xué)活動(dòng)，把學(xué)生的學(xué)置于問題之中，使整個(gè)教學(xué)過程轉(zhuǎn)化為學(xué)生“發(fā)現(xiàn)問題、提出問題、解決問題、發(fā)現(xiàn)新問題”的能力培養(yǎng)過程。這樣通過創(chuàng)設(shè)問題情景，使教學(xué)活動(dòng)在知識和情感兩條主線的相互作用下完成，使知識通過情感功能更好地被學(xué)生接受、內(nèi)化，進(jìn)而取得了意想不到的教學(xué)效果。

五、巧設(shè)疑，重回歸，增加引入探究性

情境設(shè)計(jì)中的問題要能具有探究性，要能催生生動(dòng)課堂，創(chuàng)設(shè)一個(gè)個(gè)“客觀實(shí)際的需求”的引入問題，提供給學(xué)生具體的、可感知的、可挑戰(zhàn)的數(shù)學(xué)活動(dòng)素材，激活、驅(qū)動(dòng)學(xué)生的探究欲望，促進(jìn)學(xué)生主動(dòng)地思考，讓學(xué)生真正通過自己實(shí)質(zhì)性的思維活動(dòng)來獲取知識，明確所學(xué)知識來自何方，去往何處。

案例5：蘇教版必修1第三章《對數(shù)函數(shù)的概念》，本節(jié)課是研究過指數(shù)函數(shù)和對數(shù)運(yùn)算之后的概念講評課，為了讓學(xué)生體驗(yàn)、揭示知識的發(fā)生、發(fā)展的過程，突破知識生成的瓶頸，合理有序建構(gòu)知識體系是數(shù)學(xué)概念教學(xué)的核心任務(wù)。概念教學(xué)不僅僅是讓學(xué)生明白知識“是什么”，更重要的是“為什么”，為了凸顯這兩個(gè)目的，強(qiáng)化課程引入的探究性原則，我這樣設(shè)計(jì)的本節(jié)課的引入：

問題1：光在某種介質(zhì)中傳播，每經(jīng)過1厘米，其強(qiáng)度減弱為原來的一半，假設(shè)最初的強(qiáng)度是1，

（1）經(jīng)過2厘米后，強(qiáng)度是多少？

（2）經(jīng)過x厘米后，強(qiáng)度y是多少？

（3）經(jīng)過多少厘米后，強(qiáng)度為0.125？

（4）經(jīng)過多少厘米后，強(qiáng)度為16呢？

問題2：方程（12）x=16的解存在么？是多少呢？

問題3：方程（12）x=16的解我們沒有辦法用現(xiàn)有的“數(shù)”來表示，但是這樣的數(shù)又客觀存在，回憶一下我們從小學(xué)到初中數(shù)學(xué)的學(xué)習(xí)過程中，有沒有遇到這種“危機(jī)”？

案例5的引入是概念教學(xué)課的典型代表，概念教學(xué)關(guān)乎體驗(yàn)，關(guān)乎理解，關(guān)乎學(xué)生能否全身心投入到有意義的學(xué)習(xí)生活中去。巧妙設(shè)疑，喚起學(xué)生的注意力。講課時(shí)，恰當(dāng)?shù)卦O(shè)疑可以給抽象的語言增添催化劑，喚起有意注意和無意注意，刺激大腦興奮中樞，使學(xué)生處于興奮狀態(tài)。創(chuàng)設(shè)有利于概念生成的現(xiàn)實(shí)背景和一個(gè)讓學(xué)生想做、適合做、又值得做的學(xué)習(xí)情境，學(xué)習(xí)活動(dòng)的創(chuàng)設(shè)要立足于學(xué)生的主動(dòng)探究，支持學(xué)生最好的表現(xiàn)，突出發(fā)展學(xué)生的認(rèn)知力，要讓學(xué)生經(jīng)歷他們所應(yīng)該經(jīng)歷的學(xué)習(xí)過程。在活動(dòng)過程中，要留給學(xué)生充分感知、體驗(yàn)的時(shí)間和“思”“想”的空間，提供多元互助交流、合作探究的機(jī)會(huì)，再通過學(xué)生自己的理解以及固化與內(nèi)化的歷練，積累豐富的概念活動(dòng)認(rèn)知和經(jīng)驗(yàn)，為突破概念生成的瓶頸積蓄智慧的力量，進(jìn)而實(shí)現(xiàn)高效課堂的最終目標(biāo)。作為概念講評課，在課堂設(shè)計(jì)上要充分尊重學(xué)生的認(rèn)知基礎(chǔ)，課堂引入要有梯度，指向思維的“最近發(fā)展區(qū)”；要能滿足學(xué)生心理上“探個(gè)究竟”的愿望和訴求，思維處在“憤、悱”的境地，自然而然，學(xué)生想做、樂意做又能做。

課堂教學(xué)的情景引入方式有很多，無論是故事引入、活動(dòng)引入、問題引入、復(fù)習(xí)引入、隨即引入等方式，只要能運(yùn)用恰當(dāng)、巧妙都不失為好的導(dǎo)入方式，要真正激發(fā)學(xué)生的學(xué)習(xí)動(dòng)機(jī)和好奇心，培養(yǎng)學(xué)生的求知欲望，調(diào)動(dòng)學(xué)生學(xué)習(xí)的積極性和主動(dòng)性，提高學(xué)生運(yùn)用知識解決實(shí)際問題的能力，同時(shí)又能使平淡的課堂教學(xué)豐富多彩，生動(dòng)活潑，另外，對教師也提出了更高要求，不僅自己要刻苦鉆研、精心設(shè)計(jì)，而且要經(jīng)常向別人學(xué)習(xí)，學(xué)習(xí)別人先進(jìn)的教學(xué)方法和設(shè)計(jì)思路。當(dāng)然，正如前文所提，我們很難兼顧所有原則，只要我們能合理分析教學(xué)內(nèi)容，明確本節(jié)的重點(diǎn)、難點(diǎn)，我們是可以借鑒或創(chuàng)造一些精彩的情景引入來調(diào)動(dòng)學(xué)生的學(xué)習(xí)熱情，轉(zhuǎn)變學(xué)生從知識學(xué)習(xí)的“無精打采”到“亟不可待”。

[參考文獻(xiàn)]

[1]普通高中課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書.數(shù)學(xué)（必修1，2，5）[M].江蘇教育出版社，2013.

[2]涂榮豹，王光明，寧連華.新編數(shù)學(xué)教學(xué)論[M].上海：華東師范大學(xué)出版社，2006（09）.

[3]劉祖希.倡導(dǎo)用學(xué)生熟悉的事物導(dǎo)入新課[J].中學(xué)數(shù)學(xué)月刊，2002（06）.

[4]董毓興，李靜.突破概念生成瓶頸的教學(xué)實(shí)踐與思考[J].數(shù)學(xué)通報(bào)，2014（09）.

[5]施文娟.發(fā)揮問題情境教育在數(shù)學(xué)教學(xué)中的作用[J].寧波大學(xué)學(xué)報(bào)（教育科學(xué)版），2001（03）.

[6]郭長河.精心設(shè)計(jì)高中數(shù)學(xué)課堂 培養(yǎng)學(xué)生良好個(gè)性品質(zhì)[J].科教文匯，2012（08）.