培養自主探究 促進學力提高

李霞

[摘 要]數學的教學過程就是探索的過程。教師應最大限度地給學生自主探究的機會，通過創設情境，激發探究興趣；搭建平臺，提供自主探究機會，從而引導學生在新舊知識銜接處、意見分歧處自主探究，不斷提高學生的自主探究能力，促進學生數學學習能力的提升。

[關鍵詞]自主；探究；學力；提高

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2017）29-0070-02

布魯納曾說：“探索是數學的生命。”這句話表達了兩層意思：一是數學是人們在探索的基礎上創造出來的，不經歷探索就不可能創造出數學知識；二是人們學習數學需要經歷探索的過程，不經歷探索就不能理解和掌握數學知識。基于這樣的理念，小學數學課堂教學應為學生創造更多自主探究的機會，讓學生在自主探究中體驗、感悟、理解和掌握數學知識，并在探究過程中培養學生的思維能力、創新意識和創造能力，形成積極的情感、態度和價值觀。那么，教師應如何培養學生自主探究能力呢？

一、創設情境，激發學生探究興趣

托爾斯泰曾說：“成功的教學所需要的不是強制，而是激發學生的興趣。”學生只有對數學感興趣，才能激發其強烈的求知欲，才能變“要我學”為“我要學”。因此，教師在教學中要根據學生的心理特點創設既符合知識特點、又能有效調動學生學習興趣的教學情境，以激發學生的好奇心和求知欲，吸引學生的注意力，使學生積極主動地投入到數學探究之中，從而提高課堂學習效率。

例如，在教學蘇教版教材第六冊中的“年、月、日”時，教師可以創設貼合學生實際的情境展開教學。

師：生1，今年你幾歲了？過了幾次生日？

生1：我今年10周歲，過了10次生日。

師：其他同學呢？

……

師：有一位小朋友，今年12周歲，但是他只過了3次生日，你們知道這是為什么嗎？

生2：一定是他忘記過生日了。

師：不是他忘記過生日，而是他在有的年份里沒有生日，沒辦法過生日。

生3：這是為什么呢？

此時，學生的積極性一下子就被調動了起來，在強烈的好奇心和求知欲的驅使下，學生迅速投入到了觀察年歷表、研究年歷表的活動中。

二、搭建平臺，提供自主探究機會

完全依靠教師的講解，然后讓學生死記硬背或進行機械式的重復練習的傳統教學模式，并不能提高學生的學習能力。教師要幫助學生在“理解”上做文章，讓學生動手實踐、自主探究、合作交流，經歷知識的發生、發展、變化的動態形成過程，只有經歷這樣的過程，學生才能學到活的知識。因此，在課堂教學中，教師不能扮演“傳教士”的角色，要多為學生搭建自主探究的平臺，多提供探究的機會，讓學生在探究中知道知識的來龍去脈、明白其中的道理，形成對數學知識的深刻感受。

1.在新舊知識銜接處讓學生自主探究

如，在教學“平行四邊形的面積”時，教師可以分四步引導學生進行探究。

（1）探究面積與什么有關系。

師：（出示等底不等高的兩個平行四邊形，如圖1）比較這兩個平行四邊形，哪一個的面積大？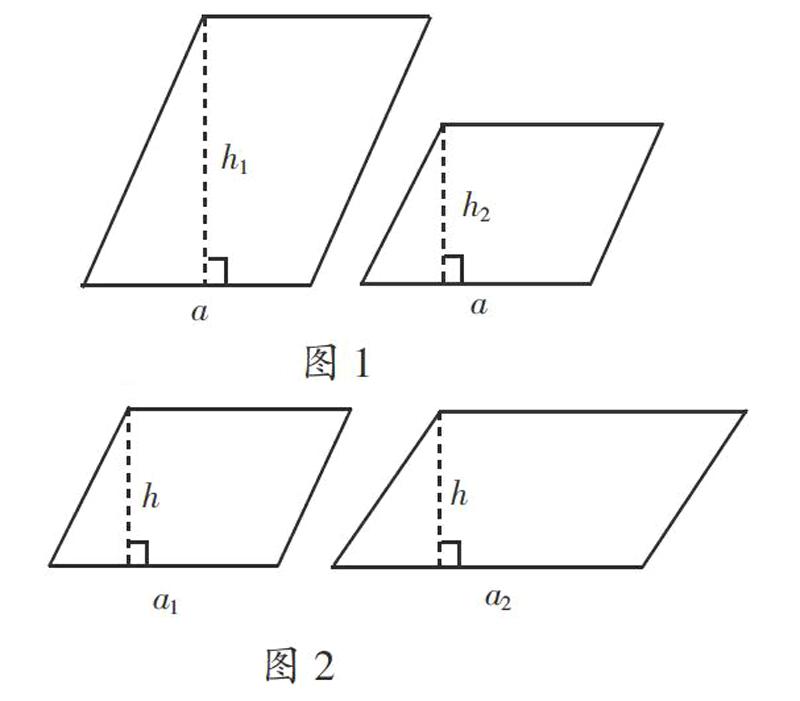

生1：高長的那個平行四邊形的面積大。

師：（出示等高不等底的兩個平行四邊形，如圖2）現在又是哪一個的面積大？

生2：底長的那個平行四邊形的面積大。

師：通過上面的比較，你們發現平行四邊形的面積與什么有關系？

生3：與平行四邊形的底和高有關系。

（2）探究轉化的方向。

師：平行四邊形的面積與它的底和高有什么關系？你打算怎樣研究呢？

生1：可以把這個平行四邊形轉化成長方形來研究。

師：為什么要轉化成長方形，而不轉化成三角形來研究呢？

生1：因為我們已經學過了長方形的面積計算，所以將平行四邊形轉化成長方形后就可以算出它的面積。如果轉化成三角形，我們還不會計算三角形的面積，就不能推導出平行四邊形的面積。

（3）探究轉化的方法。

師：怎樣把平行四邊形轉化成長方形或正方形呢？

（先引導學生獨立思考并操作，再讓同桌的學生交流討論，最后全班匯報）

生1：將平行四邊形轉化成長方形的方法——先畫出平行四邊形的高，再沿高將平行四邊形剪成兩部分，最后平移其中一部分拼成一個長方形。（如圖3）

（4）探究面積公式。

師：轉化后的長方形與原來的平行四邊形有什么關系？

（讓學生對照剪拼的圖形進行探究）

生1：轉化后的長方形的長與原來的平行四邊形的底相等，長方形的寬與原來的平行四邊形的高相等，轉化后的長方形的面積與原來的平行四邊形的面積相等。從而推導出平行四邊形的面積=底×高。

在這樣的探究活動中，學生不但對平行四邊形的面積計算公式有了深刻的認識和充分的理解，而且有效地培養了學生的觀察能力、操作能力、思維能力及推理能力。

2.在意見分歧處讓學生自主探究

由于不同的學生有不同的生活經驗、基礎知識和思維方式，所以即使是同一個班級的學生，對某個問題的認識也常常會存在分歧，這就需要教師加以引導、啟發和點撥，在學生獨立思考并形成初步認識的基礎上組織學生進行辯論。學生在辯論中互相啟發、取長補短，實現群體思維資源的共享，從而使學生深刻理解并牢固掌握數學知識。endprint

如，教師出示“租車出游”例題：“學校組織學生外出秋游，一共有420個學生參加。每輛大客車限坐50人，租金250元；每輛小客車限坐30人，租金160元。怎樣租車最劃算？”學生通過研究得出兩種租車方案：方案一是由于大客車比小客車的單人票價便宜，所以全租大客車420÷50≈9（輛）；方案二是租小客車沒有座位浪費，所以全租小客車420÷30=14（輛）。在不計算每一種方案各需要花多少錢的前提下，讓學生判斷哪種租車方案劃算。學生都認為自己的方案劃算，于是教師放手讓學生辯論，看能否想辦法說服對方。

生1：如果租大客車，平均每人要花250÷50=5（元）；如果租小客車，平均每人要花160÷30>5（元）。因為大客車的單人票價更便宜，所以應全租大客車劃算。

生2：不對！雖然大客車的單人票價更便宜，但是一共要租420÷50≈9（輛）大客車，就浪費了50×9-420=30（個）座位，因此并不劃算。

生3：我算過了，如果全租大客車，一共要花250×9=2250（元）；如果全租小客車，一共要花160×14=2240（元）。因此，全租小客車劃算。

生4：我認為全租小客車還不是最劃算的，因為租小客車雖然沒有浪費坐位，但是租小客車每人花的錢要比租大客車的貴。

生5：我覺得解決這個問題，既要考慮不浪費座位，又要考慮租一些座位相對便宜的大客車。

生6：我知道怎么思考了，就是大客車和小客車都租，并把坐兩種車的人數湊成420人，因為50×3+30×9=420（人），所以租3輛大客車和9輛小客車最劃算，一共要花250×3+160×9=2190（元）。

生7：這還不是最劃算的，大客車還可以再多租一些。因為50×6+30×4=420（人），所以租6輛大客車和4輛小客車最劃算，一共要花250×6+160×4=2140（元）。

師：通過探究，你有什么話想對全班同學說？

生8：解決這道題目時，想做到最劃算就要先從兩個方面考慮——一是盡量多租便宜的車，二是不要浪費座位。然后列出適合的租車方案，再算一算每種租車方案的租金是多少，最后按租金判斷怎樣租車最劃算。

事實勝于雄辯，學生在思考中辯論，在辯論中再思考，學生之間相互吸收他人有價值的思維成果，不斷完善和充實自己，最終明白了租車問題中的學問，掌握了租車的思維方法。在這個教學過程中，學生解決的不僅僅是一個租車問題，而是解決了類似于租車問題的思考方法，不但拓展了學生解決問題的思路，而且有效地訓練和發展了學生的思維能力。

總之，要實現新課程提出的數學教育目標，教師必須要轉變觀念，變數學教學為數學教育，同時，教師還必須改變傳統的教學方式，變講授式教學為探究式教育模式，課堂上多為學生提供自主探究的機會，讓學生在情境中發現問題、提出問題、探究問題，在解決問題的過程中理解和掌握數學知識，培養學生的創新意識和創造能力，從而不斷促進學生數學學習能力的提高。

（責編 李琪琦）endprint