老調新彈，平中出奇

楊永鐸

[摘? 要] 數學中有不少陳年舊題，其實這些舊題中蘊藏著可貴的教學資源，如果教師巧妙地加以利用，定會讓課堂因此而精彩！本文結合筆者的教學實踐，總結出了幾條讓陳年舊題富有新意的對策.

[關鍵詞] 數學課堂;問題設計;舊問題;新思路

課堂問題是依據教學目標、教學內容、教學重點及難點，把主要的學習內容預設成具體且有待解決的問題. 一個好的課堂問題，不僅能充分調動學生的學習積極性，讓他們掌握、鞏固數學知識，而且能及時地反饋教學信息，促進教學改革，做到有的放矢地因材施教，發展學生的數學思維品質.

其實很多傳統的數學問題在教師看來已是陳年舊題，年年出這些題，教師自己也會有倦怠之感，所以總想找一些新題，可變來變去，往往也只能改變一下數據. 那怎樣才能讓這些陳年舊題變出新意呢？筆者結合自身幾年的教學實踐，從中總結出了以下對策.

舊題新用，以不變應萬變

舊題，總是用在過去出現的地方，就會平淡無奇. 學習“二元一次方程”時，教師可在黑板上給出一個問題：一棵樹上有10只鳥，一位獵人向樹上放了一槍，這時樹上的小鳥和不在樹上的小鳥各有幾只？此題一出，五花八門的答案便蜂擁而至.

大家都明白，學生從小學到初中，這個問題已經接觸過不下三次，小學時出現也許是為了訓練創新思維，而此處出現又是出于什么目的呢？這道題的很多答案已經超出了數學思維的范疇，各種所謂的創新早已讓人生厭，如假如樹枝勾住了打死的鳥;假如這槍是無聲手槍;假如這些鳥是聾的……所有的這些假如似乎都是一種鉆牛角尖，但無論答案是多少，如果用方程思想去理解的話，等量關系為“樹上的小鳥只數+不在樹上的小鳥只數=10”. 進一步，可設樹上的小鳥有x只，不在樹上的小鳥有y只，于是可以得到方程x+y=10，從而導出二元一次方程的定義. 此時學生的很多想法與爭論已不被大家關注，學生關注的是用方程方法把所有答案都網羅其中. 可見，把舊題與新內容結合起來，在該使用處及時使用，有時竟能出現新的一片天地，讓舊題因新知而豐滿，讓新知因舊題而生動.

老題新解，以悟通超越聽懂

明代程大位所著的《算法統宗》里有一道名題《百僧百饃》：一百饅頭一百僧，大僧三個更無增，小僧三人分一個，大小和尚各幾丁. 題意是：有一百個和尚吃一百個饅頭，大和尚每人吃三個，小和尚每三人吃一個，問大小和尚各有幾人.

此題出現在了人教版小學四年級的思考題中，小學教參里一般采用假設法：假設100人都是大和尚，則可以吃饅頭3×100=300個，比實際多吃了300-100=200個，之所以多出來200個饅頭，是因為把其中的小和尚換成了大和尚，現在換回去，每次三個小和尚換成三個大和尚，饅頭就增加3×3-1=8個，所以這多出的200個饅頭需要換200÷8=25次，所以換成大和尚的小和尚的人數是25×3=75，大和尚的人數是100-75=25. 非常難懂吧？不要說小學生，就是初中數學教師都有墜入云海的感覺. 如果把這種解法講給初中生聽，估計95%的學生聽不懂. 既然聽不懂，那數學教師最好不講，教給他們方法即可. 好在到了初中，解決問題的方法多了，而且不少方法還體現了一定的數學思想.

初一時，利用方程思想可以這樣解答：設大和尚有x人，則小和尚有（100-x）人. 根據題意有3x+（100-x）÷3=100，解得x=25. 又100-25=75，所以大和尚有25人，小和尚有75人. 當然，也可以設小和尚有x人，然后運用一元一次方程來解，這種方法與設大和尚的人數為x的方法類似;還可以設小和尚有x人，大和尚有y人，通過列二元一次方程組來求解.

學生通過對這一名題多種求解方法的嘗試，能品嘗到成功的體驗，能把數學思想與經典舊題結合起來，能解除學生過去的理解之痛.

到了初二，筆者又給學生講起了這道題，不過這次是為了幫助學生建立問題解決的轉化思想——此時學生已有解決“雞兔同籠”問題的經驗. 具體思路如下：由于小和尚三人吃一個饅頭，每人只吃三分之一個饅頭，思考起來比較吃力，不妨將所有大饅頭都切割成三個小饅頭，于是問題就變成：三百饅頭一百僧，大僧九個更無增，小僧一人分一個，大小和尚各幾丁. 然后利用前面講過的方法去思考——比如“雞兔同籠”問題中的假設法，這種解法會省去分數參與思考的麻煩，使問題變得更為明朗.

初三復習時，筆者再次將這一問題搬入課堂，這次是為了復習函數.

問題1：請問100個和尚中除了大和尚都是小和尚，設大和尚有x人，那么小和尚的人數y與大和尚的人數x之間有什么函數關系？

（由于總數不變，大和尚增加就意味著小和尚減少，有學生就誤認為這是反比例函數. 不過也好，這正是展開討論，趁機復習函數基礎知識的良機. 當學生列出解析式以后，筆者又讓學生說說這是什么函數，為什么.）

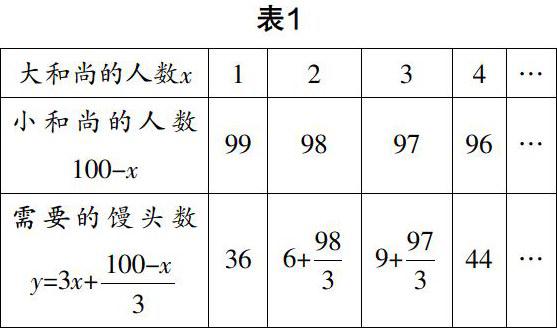
問題2：如果有100個和尚，按大和尚有x人，每人吃3個饅頭，小和尚每3人吃1個饅頭來算，這100個和尚需要吃的饅頭數y有幾種情形？我們可以通過列表來分析（如表1）. 你能在坐標系中找到這些點（x，y）嗎（利用畫圖軟件）？這些點在坐標系中的位置有一個什么特點？

問題2擺脫了原題的問題框架，再一次強化了函數是一個量隨著另一個量的變化而變化的，這一問題能讓學生再一次經歷先描點再連線的函數圖像形成過程，同時能再次鞏固一次函數圖像是一條直線的性質.

問題3：如果你想找到饅頭數正好是100的情況，有一種特殊的方法，請看問題2中的圖（圖略），你能找到這個我們需要的點（x，y）嗎？此時這個點的坐標與方程之間有什么關系？

同一個問題，從小學四年級到初三多次出現，每次出現的目的都不相同. 學生通過不同的數學知識與數學思想，可以把同一問題逐漸明朗化、簡便化，這能讓他們感覺數學確實是解決實際問題的強有力工具. 通過這樣多年的時間穿越，學生對數學學習的感情會與日俱增. 這種做法與有的教師所采用的題海戰術相比，有天壤之別！

舊題新編，以全面克服片面

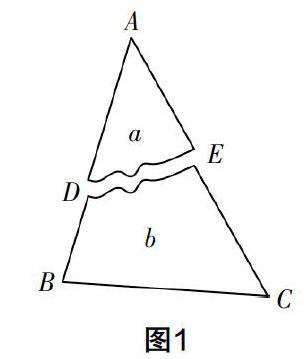
教學“全等三角形的判定”時，教師給出了一道選擇題：某塊三角形玻璃碎成如圖1所示的兩塊，如果照原樣到店里配一塊，只要帶哪塊去就行了？（?）

A. a? ? ? ? ? ? ? ? ? ? ?B. b

C. a和b? ? ? ? ? ? ? ? D. 哪塊都不行

對于此類三角形玻璃問題，很多教師都接觸過，而且學生能輕而易舉地得出答案，但有為數不少的學生認為選B是因為玻璃b的兩條斷邊可以補出來. 其實這背后蘊藏的數學原理就是三角形全等——玻璃b屬于“ASA”的情形，可見這一題的設計并沒有發揮出其應有的價值. 如果教師把題稍改一下：“某塊三角形玻璃碎成如圖1所示的兩塊，裂口符合下列特征：AD=2BD，AE=EC，如果照原樣到店里配一塊完整的玻璃，只要帶哪塊去就行了？”加了條件后，AB與AC的長度可以分別由AD與AE按關系延長適當長度而得到，這樣就又多了一種“SAS”的解決方法，答案就顯得比較開放了. 可見，活學活用在這兒得到了比較充分的體現.

再進一步，如果不想帶玻璃，有沒有辦法買到需要的玻璃呢？試想：我們都有手機，拍個照去行不行？如果不行，需要量幾條邊的長度才行？如果沒有手機，光用尺子量的方法，又需要量幾條邊呢？這樣一來，問題的開放性更得到了充分的體現，而且把全等三角形的所有情況都納入這一題中了，使訓練具備了足夠的厚度.

綜上所述，舊題中蘊藏著可貴的教學資源，陳年舊題一如陳年老酒，只要巧妙地改，準確地用，慢慢地品，就會令師生如沐春風，讓課堂精彩無限！