化錯：從診斷學生的真實錯誤開始

摘要：“化錯”就是變化錯誤，幫助學生走向正確的學習道路。精彩的“化錯”教學更能體現一位教師的教學智慧，體現教師面向全體的教育情懷。但現在一些看似“精彩”的化錯教學，不是面對學生真實的錯，而是來自書本的錯和教師臆想的錯，從而使化錯失卻了針對性。如何發現學生在學習中真實的錯？課前進行學情調查、課中創設融錯空間、課后建構合理的診斷系統，是一條行之有效的路徑。

關鍵詞：小學數學；化錯 ；真實錯誤；診斷

中圖分類號：G623.5 文獻標志碼：A 文章編號：1673-9094（2017）11B-0040-04

“化錯”一詞源自華應龍老師的“化錯教育”。“化”指變化，“化錯”就是變化錯誤，幫助學生走向正確的學習道路。一節真實的課堂，學生不可能不出現錯誤。如果說以前的課堂更多的是追求一種精致，一種滴水不漏般的正確，那么現在的課堂上老師們更樂意將錯誤轉變成課堂的亮點。因為精彩的“化錯”教學更能體現教師的教學智慧，體現教師面向全體的教育情懷。

當然，我們也看到，在一些日常課特別是公開課上，精彩的“化錯”教學卻忽略了真實的學習過程，而淪為一種重形式的作秀。

案例一：

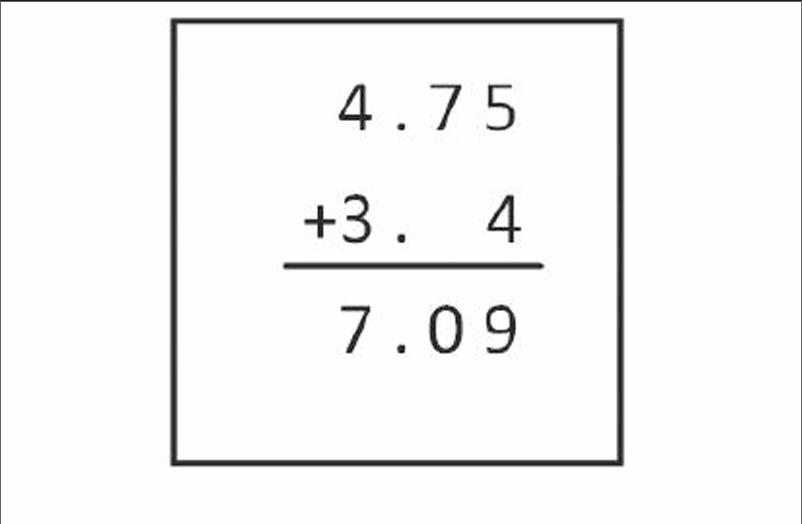
五年級上冊《小數加減法》例1，創設情境后，教師安排學生嘗試計算4.75+3.4，并在教材中出現了兩種算法：

上一節課上，教師進行了“嘗試計算—兩種算法判斷—比較說明算理”的教學過程。在交流環節，當學生討論了第一種正確的做法后，教師反復問：“還有沒有不一樣的做法？”沒有學生回答。一陣沉默后，教師拿出了書上的第二種錯誤的做法，說：“老師這里也有一種做法，大家一起來判斷一下對不對。”學生一致回答：“錯。”老師又問：“錯在哪里呢？”學生說：“小數點沒有對齊。”

一、化錯：應該面對學生真實的錯

我們來剖析一下上述案例，為什么教師會將不是學生“錯誤”的錯拿來大做文章呢？

1.教材本位：書上的都是對的

我們現行使用的教材是由許多專家、經驗豐富的教師和教學研究人員合作編寫出來的，他們不僅諳熟我國數學課程的歷史和現狀，把握了新課標的要義，而且對國際數學課程發展的潮流有著相當深的理解和把握。對教師來說，教材是主要的教學資源，是教與學的重要依據。[1]因此，我們在教學前首先要認真鉆研教材，吃透教材的編排意圖，但這并不意味著就應該唯教材論。古人早就說過：盡信書，則不如無書。教材上出示的方法是具有代表性、典型性的方法，但不同地區、不同學校學生的多樣性也使得教材不可能窮盡所有方法。教材本位主義者認為：教材就是標準，書上講的方法就一定要展示，書上的錯誤就是學生的代表性錯誤，即使學生沒有出現這類錯誤，也一定想辦法出示。正如“案例一”中的那樣，學生沒有這類錯誤，教師自己就拿出來，或課前約定讓學生故意犯這類錯誤，或假意說隔壁班有同學這樣做的。因為不是來自學生出現的真實的錯誤，糾錯便缺失了針對性，學生參與意識不強，刻意編制的錯誤反而影響了他們已有的正確認知。而且，因為教師只想強調書上這種典型錯誤，反而忽略了學生產生的真實錯誤。如上述案例中，筆者聽課時坐在旁邊的小男生是這樣做的：

當老師首先展示正確的做法后，這位同學意識到了自己的錯誤，所以老師反復問還有沒有不同的做法時，他不敢展示自己錯誤的做法了。如果教者能夠在鉆研教材的同時，理清本節內容在小學數學教學中所處的位置，就會發現：沒有發生書上的典型錯誤是很正常的。追溯學生對小數的認識過程就可以發現，他們在三年級下學期已初步認識小數，并學過用豎式計算一位小數的加減法。在當時的教學中，雖然沒有完整概括小數加減法的計算法則，但稍有數學知識的教師都會強調列豎式時“小數點對齊”，而不會說成“只要末尾對齊”。因為，老師們都知道，三年級只學一位小數的加減法，“小數點對齊”和“末尾對齊”雖是一回事，但為了與后續學習相銜接，都會強調“小數點對齊”。因此，到五年級再次學習“位數不同的小數加減法”時，學生也能正確地遷移“小數點對齊”的算法，只是對于“為什么小數點對齊”卻一知半解 [2] 。基于以上分析，學生對“小數點對齊”的算法并非一無所知，反而是早已熟悉，這也就是導致他們沒有出現書上典型錯誤的主要原因。

2.教師本位：“我”想的就是學生想的

對學生錯誤的精彩轉化，有時來自教師長期積累的教學智慧，但更多的來自教師課前充分的預設。尤其在嘗試教學、探究性學習時，常常需要根據以往的教學經驗猜測學生可能出現的種種生成情況，包括可能出現的各種錯誤。經驗豐富的教師一般猜得很準確，但既然只是一種課前預想，那么學生的課堂生成有可能在意想之中，也可能是意料之外。如“案例二”中，教師想通過展示錯誤的做法引起學生的注意：異分母分數加減法不可以將分子、分母分別相加，而應該尋找新的方法解決，并且學會從結果來估計結果的正確性。教師在巡視后發現沒有這種預設中的錯誤，只好自己出示這種錯誤請學生辨析。那么，學生為什么不會出現這類錯誤呢？在學習異分母分數加減法前，他們學過了同分母分數加減法，教學時，教師往往會問：“同分母分數加減法，為什么分母不變，只要將分子相加減呢？”學生就理解了其中的道理：分母相同，是分數單位相同，也就是每一份的大小相同，只要將分子所代表的份數直接相加。當學生遇到異分母分數加法時，首先會和同分母分數加法作比較，思考如何把分母也變成相同的，再用學過的知識來解決新問題。而教師出示的錯誤，只有對分數的意義和同分母分數加減法完全不懂的人才會這樣盲目相加。教師本位主義者在教學時常以教案為中心，以自己所想代替學生所想，認為憑經驗預想的就是學生會出現的情況，所以當學生的生成在意料之外時，仍然拘泥于教案設計，把教師臆想的錯誤當成學生的錯誤。

二、化錯：如何發現學生真實的錯

學生學習中的“錯”可以生成新的學習資源，應該已成為大家的共識。但這種“錯”應該是來自學生真實的“錯”，而不是書本上的錯，更不是老師臆想中的錯。只有面對學生真實的“錯”，進行適切的轉化和提升，才能有助于學生數學知識的掌握、數學能力的提升。endprint

如何發現學生真實的“錯”呢？

1.基于調查的學情分析，預設潛在錯誤

美國心理學家奧蘇伯爾在其著作《教育心理學》中寫道：“如果我不得不把全部的教育心理學還原為一句話，我將會說，影響學習的唯一的、最重要的因素，是學生已經知道了什么，我們應當根據學生原有的知識狀況去進行教學。”因此，我們在設計教學方案前，有必要通過調查，全面了解學生的所知、所惑、所錯，所需。其中很重要的一點，就是通過調查了解學生學習新知可能出現的典型性錯誤，使教者心中有數，應對有底。如“案例一”中，教師可以在課前選取各層面有代表性的學生若干，在沒有任何提示的情況下嘗試用豎式計算一道小數加減法，了解學生可能的解法，并通過對話的方式詢問學生這樣計算的想法。如果這些代表學生中沒有出現書上典型的錯誤，教師就要思考“為什么”了。這樣提前思考，就可能避免課堂上生硬地展示“錯誤”。同時，通過這樣的課前調查，還可以發現學生的其他錯誤算法和想法。

課前調查除了分層抽樣，還可以整體抽樣，采用的方式一般是問卷或訪談。如一位老師在上“角的初步認識”時設計了如下問卷題：（1）你能在生活中找到角嗎？（2）角是怎樣的？請你畫下來。調查后發現對于問題（1）， 96.3%的同學能找到生活中的角，但50%左右的學生找的不是數學意義上的“角”，而是房間的角落、幾何體的頂點等等，說明學生還不能區別生活中的“角”和數學上的“角”。根據學生的這一錯誤認識，教學時就要突出將生活中物體面上的角抽象的過程。抽象之后，還要引導學生正確地指一指，比較這些抽象出的圖形的共同特征，從而使學生形成對數學上“角”的正確認識，以區別生活中的“角”。經過調研之后的教學設計，能針對學生的真實潛在問題展開教學，使“化錯”更有實效。

2.創設容錯的學習空間，發現生成錯誤

差錯在課堂中無時不在，但部分教師害怕出差錯，一味去堵，去回避，學生真正的生成性錯誤就無法展現。在有容錯空間的課堂上，孩子們不怕出錯，他們享受錯誤，懂得“錯誤是創造的開始”，所以當他們出錯了，也敢于展示自己的錯誤，說出自己錯誤背后的真實想法，更敢于自我糾錯。因此，創設容錯的學習空間，教師應有容錯的雅量和情懷，認識到“自古成功在嘗試”，讓孩子們試錯，其實就是在嘗試，在求真，坦然面對學生的錯誤，才有可能機智地進行點化。

首先，教師要有發現錯中蘊藏著亮點的眼光。例如有位老師在上二年級《角的認識》一課時，出示兩個角讓學生嘗試判斷哪個角大，哪個角小。老師問：“你們可以用什么工具來比較這兩個畫在黑板上角的大小呢？”一位同學高舉著小手搶著說：用尺量。老師很驚奇，讓這位同學上臺演示。這位同學將長尺對準角兩邊畫的端點處，量了兩端點之間的距離。雖然他的辦法是錯的，但老師還是微笑著對他和同學們說：“我們量長度是用尺子量，他想到量角的大小也可以用尺子，其實是想用尺來量出角的兩邊叉開的大小。角兩邊叉開的大小決定了角的大小，我們手邊的哪個工具更容易量出這兩個角的邊叉開的大小呢？”學生自然就想到了活動角。在這里，雖然學生的量法是錯誤的，但老師獨具慧眼，敏銳地捕捉到錯誤中的“正確”因子，引領學生繼續走向學習的關鍵之處。

其次，教師要給予學生改錯的機會。例如在教學“萬以內數的讀法”一課，當學生根據計數器寫出3052這個數時，小朱同學讀成了“三千五十二”，立刻被同學們的反對之聲淹沒。他也意識到可能是自己讀錯了，漲紅著臉坐了下去。我不置可否，繼續請另一位小陳同學讀。我轉向小朱，問：“聽出你倆讀法上的不同之處了嗎？”小朱說，小陳讀出了零，他沒有讀出中間的零。我表揚他善于傾聽后繼續問：“讀三位數時，中間的零要讀嗎？”他肯定地點點頭。“對了，這里的四位數中間有0，也要讀。”我接過話，并請他再讀一遍，他聲音響亮地讀對了。我轉向全班同學說：“看，學習就是不斷糾正錯誤的過程，今天小朱同學又學到新知識了，那就是讀四位數時中間的0……”同學們齊聲說：“也要讀。”這時，再看小朱同學，他再也沒有了剛才的窘迫。正是因為教者有容錯的雅量和情懷，知道每個學生有不同的學習起點，學生的錯誤也許五花八門，但老師面對學生的態度卻是一樣的和藹、一樣的溫暖、一樣的鼓勵。正是這份情感的投入，才能使學生敞開心扉，展示自己真實的錯誤，不以錯為恥，在錯誤中不斷探索，不斷前進。

3.構建合理的診斷體系，掌控既成錯誤

通過課堂練習，教師更能夠發現學生真實的錯誤，但并不是所有的真實錯誤都能在做練習時準確反映出來的。如教學平行四邊形面積的計算后，老師會出示一些明確了底和高的平行四邊形，請學生計算面積。學生可能都做得對，但有一部分并沒有完全理解為什么這樣算，只是照搬公式，模仿而已。再如，一些老師喜歡在課上聽學生齊答，看似異口同聲、完全正確，其實一部分學生卻在濫竽充數。還有，一些練習采用指名口答的方式，卻常常成了一部分思維迅速學生的表演等等。如此的課堂診斷，并不能讓老師真正了解學生的真實錯誤，因此，化錯、糾錯的針對性也就無從談起。

筆者認為構建合理的診斷體系很重要，這種體系主要包括診斷內容和診斷方式兩大方面。

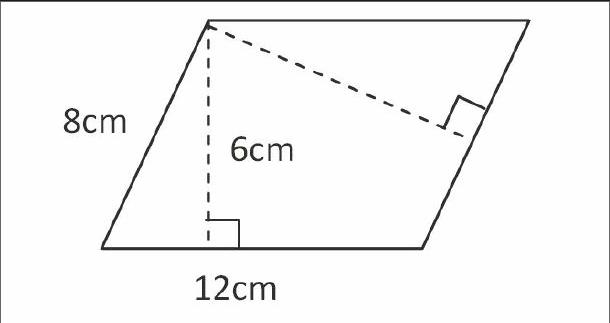
一是診斷內容要全面。既要考查學生對本課知識和技能的掌握情況，又要考查學生在學習過程中獲得的能力、方法，甚至能診斷出學生的學習態度和習慣。例如，出示：

提問學生：“怎樣計算平行四邊形的面積？為什么？”面對此題，如果學生出現8×12的錯誤，說明他還沒有理解平行四邊形面積的推導道理；如果出現8×6的錯誤，說明他不知道平行四邊形面積計算中，底和高應該是一組對應的數量。而如果學生說不出“為什么這樣計算”，說明他只是機械地模仿。多了解一些信息，對學生學習情況的診斷就更全面了。

二是診斷方式要多樣。課堂上我們通常會采用獨立練習、口答、齊答等方式進行診斷，這些各有利弊。教學中應靈活運用多樣診斷方式，既有指名口答，也有獨立練習，要增加學生獨立思考的時間，使不同的學生能夠較充分地展示自己的思考過程。要面向全體學生，有針對性地關注不同層次的學生。要多傾聽學生陳述想法，當堂訪談或課后訪談，以便了解錯誤背后真正的原因。

學生學習中產生的不可避免的錯誤，是一種新的學習資源。作為教師，應該正確面對學生真實的錯誤，包容理解學生真實的錯誤，智慧化解學生真實的錯誤，真正達到化錯育人的學習效果。

參考文獻：

[1]吳文娟.給創造性使用教材提個醒.小學教學參考[J]，2008（7）.

[2]吳文娟，俞昭英.“按圖索驥”還是“順勢而為”.中小學數學（小學版）[J]， 2013（8）.

責任編輯：宣麗華

Abstract： Mistake-changing means changing the types of mistakes to help student take the right way of learning. Excellent mistake-changing teaching can better display teachers teaching wisdom and their educational feelings. Yet， seemingly excellent mistake-changing instruction is not oriented towards students real mistakes but mistakes from textbooks and teachers imagination， which results in absence of targeted mistakes. An effective way of finding students mistakes is to pre-class diagnosis of learning， while-class designing room for mistakes， and post-class construction of diagnosing systems.

Key words： primary school mathematics； mistake-changing； real mistake； diagnosisendprint