變中思悟 探中明理

朱國軍 戴厚祥

【關鍵詞】分數;教學設計;辯證思想

【中圖分類號】G623.5? 【文獻標志碼】A? 【文章編號】1005-6009（2018）81-0061-03

小學數學的“分數”知識板塊蘊含著豐富的數學思想，有助于培養學生的辯證思維。在教學蘇教版五下《分數的基本性質》一課時，教師可以通過精心的教學設計，讓學生經歷分數基本性質的建構過程，歸納概括出分數的基本性質，運用分數的基本性質解決有關的數學問題。在此過程中培養學生觀察、分析、比較、歸納、概括及動手實踐的能力，發展學生的思維，讓學生初步體會“變”與“不變”的辯證思想。本節課的教學設計以學生的探索活動為核心，寓數學思想方法于教與學的過程之中，以“變”與“不變”為主線，以“猜想—驗證—觀察—結論”的研究過程為暗線，讓學生透過現象理解“商不變規律”“分數的基本性質”“比的基本性質”，體會其形不同而質同，感悟“變與不變”的辯證思想。

一、創設情境，引入分數

師（導入）：在“幸福嘉年華”寒假生活成果博覽展銷會上，點贊卡的數量是衡量學生表現的標準。在活動中，我統計了每組學生的參與人數和獲贊人數，如表1。

師：從表格中的數量信息看，哪個小組表現得好？

生：從各組獲贊比例看，各個小組表現都不錯。

生：我猜測，、、這三個分數可能相等。可以證明驗證一下？（教師板書：猜想）

【設計意圖】對信息的準確解讀與理解，是生成新問題的必要基礎。上課伊始，通過情境創設，以學生親身經歷的“幸福嘉年華”活動中的點贊卡引入，激發了學生探究新知的欲望，引發學生關注點贊人數與參與人數兩個數量，讓學生主動發現和應用分數。

二、自主探究，構建新知

1.猜測驗證，形象感知。

師：、、相等嗎？請你用畫一畫、折一折、算一算或文字方法，嘗試說明。

學生匯報：

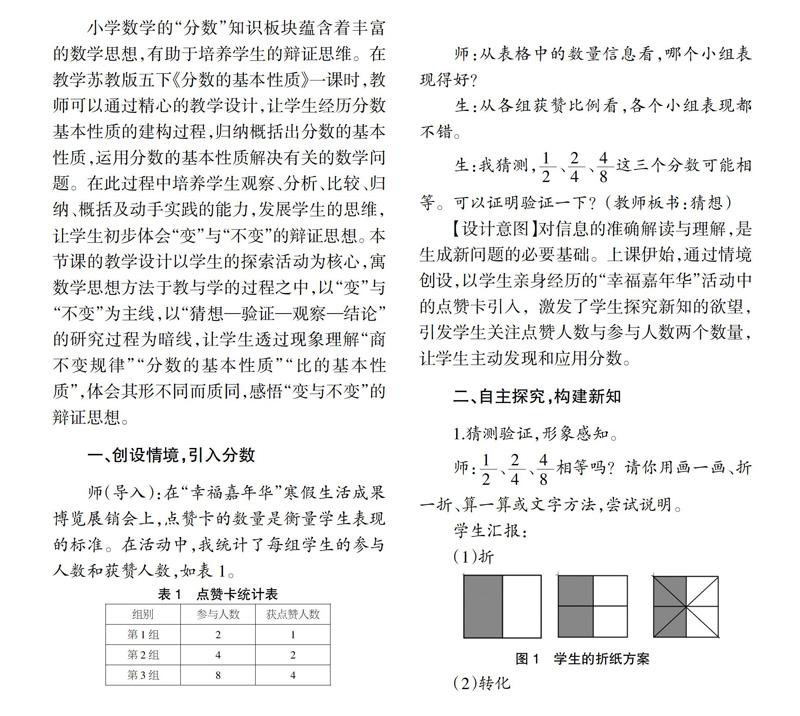
（1）折

（2）轉化

=1÷2=0.5

=2÷4=0.5

=4÷8=0.5

（3）擺

把8根小棒平均分成兩份，取其中的一份是4根，把8根小棒平均分成四份，取其中的兩份是4根，把8根小棒平均分成八份，取其中的四份也是4根。

（4）畫

師（小結）：通過不同的驗證方法我們發現：==，通過這個等式可以推出結論：分子變化，分母變化，分數的大小可以不變。（板書：驗證==）

【設計意圖】引導學生用畫一畫、折一折、擺一擺、說一說等方法初步感受分數的“變與不變”，從而對其中的變化規律產生感性的、淺顯的認識，滲透“數形結合”和“變中有不變”的數學思想方法。

2.想象列舉，深入體驗。

師：通過研究我們發現，分子分母不同，分數卻相等。你還能從生活中找到像這樣相等的分數嗎？

生1：分西瓜。同樣的西瓜平均分成4份取1份，和平均分成12份取3份是同樣多的，他們的和是相等的。（如圖3）

生2：班級的座位分組。36人平均分成3組，其中的一組是12人;平均分成9組其中的3組也是12人;平均分成36份其中的12份也是12人，也就是==。

師（小結）：通過這兩個例子，我們再次驗證：分子分母變化，分數的大小可能不變。（板書：==）

【設計意圖】通過任意舉例再次驗證，讓學生的認知從單一具體現象發展為普遍規律，深刻感受分數的“變”與“不變”，為下一教學環節中由“變”到“不變”的轉換奠定基礎。

3.觀察等式，探究規律。

師：比一比，看誰能在30秒內找出最多對相等的分數？

生1：從左向右，的分子和分母同時乘2得到了，的分子分母同時乘2得到，分數的分子分母同時乘2，分數的大小不變。

生2：從右向左，的分子和分母同時除以2得到了，的分子分母同時除以2得到了，分數的分子分母同時除以2，分數的大小不變。

生3：其他組分數道理同上。

板書：分數的分子分母都乘或除以相同的數，分數的大小不變。

【設計意圖】把分數教學的重點聚焦在學生的認知難點“分數的分子、分母怎么變，分數的大小才會不變”這個問題上，設計三次不同層次的探究活動：先創設情境引出一組相等分數讓學生驗證，再讓學生從生活中找相等的分數并驗證，最后讓學生憑直覺快速寫出相等的分數。分層次的教學設計，讓學生由淺入深地理解分數的變化規律。

4.爭論辨析，建構意義。

教師出示課件：==？

生（交流）：分子分母不能除以0，因為除數不能是0，乘0的話，分母就是0了，而分母不能為0，所以0除外。

師（小結）：分數的分子和分母同時乘或除以一個相同的數（0除外），分數的大小不變，這就是分數的基本性質。（板書：0除外：分數的基本性質）

課件演示：中國古代數學家劉徽在數學名著《九章算術》中對分數基本性質的研究。

【設計意圖】在學生知曉“分數的分子分母同時乘或除以一個相同的數，分數的大小不變”這一規律后，出示特殊情況，引導學生主動質疑相同數0是否除外，使學生在質疑、釋疑的過程中對規律有了進一步的理解，培養了他們的問題意識和嚴謹的數學學習態度。

三、拓展延伸，內化應用

出示習題：

1.寫數：你能在數軸上寫出和大小相等的分數嗎？

2.改數：你能將和改寫成分母相同的分數嗎？

3.選數：給定10個數，選出與某數相等的分數。

4.填數：=，當a等于1、2、3、4……時，b分別等于幾？a=1時，b=（ ）;a=2時，b=（ ）;a=3時，b=（ ）……

師：a與b之間的關系是什么？為什么存在這樣的關系？你怎么知道的？

【設計意圖】練習題的教學目的不能只停留在技能的掌握上，還應該關注學生的感悟、聯想和提升。“寫數”：通過在數軸上寫相等的分數，感受“值同形不同的分數在數軸上的位置一樣”的簡約和極限思想;“改數”引導學生思考將異分母分數轉化成同分母分數的規律，為以后學習約分、通分埋下伏筆，更便于分數大小比較、分數的加減運算;“填數”引導學生揭示=（a、b是不為0的自然數）中a與b的倍數關系，既鞏固了新知，又滲透了函數思想，有利于促進學生對數學的不斷思索。

四、總結內容，提煉方法

師：畢達哥拉斯曾經說過：“在數學的天地里，重要的不是我們知道什么，而是怎么知道什么。”說說看，今天你知道了什么，又是怎么知道的呢？

學生交流后總結：

1.我們知道了分數的基本性質;

2.我們通過折一折、畫一畫、想一想發現了分數的基本性質;

3.我還知道了分數的基本性質和商不變的規律具有同樣的性質……

師（總結）：我們在四年級認識了商不變的規律，今天我們又研究了分數的基本性質，到了六年級我們還會認識比的基本性質。在這樣的學習中，變化的是學習內容，不變的是數學本質規律，許多數學知識都有著變與不變的表象，而我們都是在變與不變中尋求數學規律。

【設計意圖】引導學生回顧所學知識和基本技能，反思學習過程，不僅交流知識技能方面的收獲，還著重讓學生分享學習方法、情感態度的體會，有助于學生內化、優化認知結構，感悟探究方法和數學思想，體驗主動探究獲取知識的愉悅，增強學習的動力和信心。

（作者單位：南京市南師附中江寧分校小學部;南京市江寧區教學研究室）