關注學習過程 促進思維發展

朱瑩瑩

[摘 要]】數學是“思維的體操”，無論課程改革倡導怎樣的教學方式和學習方式，數學教師都要關注學生的學習過程，為促進學生的思維發展而教。“雞兔同籠”作為新增的一個教學內容，教師可以它為載體，引導學生經歷知識形成的過程，讓學生在觀察、分析、抽象、概括的過程中積累數學活動經驗，促進學生思維的發展。

[關鍵詞]小學數學；學生思維；雞兔同籠

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2018）08-0024-02

“雞兔同籠”是我國古代著名趣題之一。以前，雞兔同籠問題只是作為小學奧數的常見題型。新課改后，不少版本的教材都新增了一個教學內容——“雞兔同籠”。人教版教材在六年級上冊《數學廣角》中詳細介紹了“雞兔同籠”問題的出處、幾種典型解法及實際應用，突出“解決問題策略的多樣化”。在北師大版教材中，“雞兔同籠”是作為研究問題的載體，意在讓學生經歷列表、嘗試和不斷調整的過程，體會解決問題的一般策略——列表。教材不僅呈現了“雞兔同籠”的情境和出處，還給出了三個表格，第一張表格是逐一列表法，第二張表格是跳躍列表法，第三張表格是取中列表法。下面就說說如何借助“雞兔同籠”這一載體，促進學生思維的發展。

一、任務導向，啟迪思維

通過課前調查發現，有少數學生在課外就已經接觸過“雞兔同籠”問題，能用假設法解決問題，但大部分學生都沒接觸過。這樣一來，如果讓全體學生都用列表法解題，已經學過的學生就會說：“我會用假設法解決問題，多快！何必用列表法。”是呀，為什么一定要用列表法呢？雖然這節課的一個教學目標是讓學生學會用“嘗試與猜測”解決問題，但是強迫學生用列表法解題，學生只會是為了列表而列表，會失去解題的動力。從大部分學生的學習起點考慮，教學目標“結合解決‘雞兔同籠的問題，借助列表法體驗嘗試與猜測的解題策略”沒有錯，但面對學習起點不一樣的學生，如何預設課堂，才能讓每個學生都能主動參與學習，思考問題呢？

分析假設法和列表法，我們不難發現，列表法是先假設雞或兔的腿數，再一個一個地進行嘗試和推算；假設法是先假設全是一種動物，再根據腿數的差距，求出只數。細細想來，假設法也是“先假設——調整——結論”，和列表法是在“做”一樣的事，從思維層次上講：假設法是列表法的一種表現形式，假設法可以看成是對列表法的進一步抽象和提升，而列表法在本質上就是假設法，列表過程的每一步都是假設。

于是，我先讓會用假設法解決問題的學生思考問題：“能不能把用假設法解題的過程記錄在表格里呢？”學生對這個新任務很感興趣，在表格里嘗試記錄假設法解題的思考過程，不敢懈怠（如表1）。接著，讓學生介紹自己的方法，解釋為什么這么快就能找到正確答案。“80-54=26（條），多了26條腿說明兔子多了13只，也就是雞要增加13只”。學生在介紹方法的過程中就能感悟到：假設法和列表法這兩種方法是有聯系的，在列表法中也能找到假設法的影子。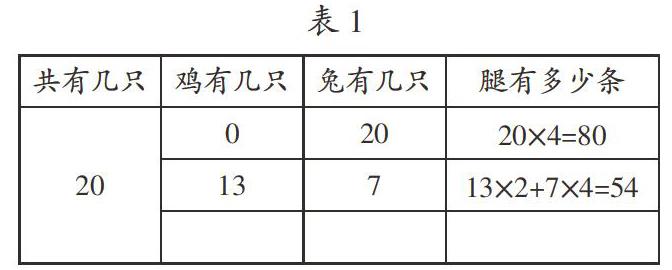

這樣的處理方式，既可以調動學生學習的積極性，使他們能夠主動地參與課堂學習，也點破了列表法和假設法之間的關系，可謂一舉兩得。

二、聚焦策略，提升思維

著名的數學教育家波利亞認為：“學習任何知識的最佳途徑，都是由自己去發現、探究，因為這種理解最深刻，也最容易掌握其中的內在規律、性質和聯系。”因此，教師要有效引導學生經歷知識形成的過程，讓學生在觀察、辨析、判斷、分析、抽象、概括等具體的數學活動中積累基本的數學活動經驗，提升數學思考的能力。

在引導學生借助表格進行猜測與嘗試解決“雞兔同籠”問題時，除了給出教材上介紹的三種方法“逐一列表法、跳躍列表法、取中列表法”，還可介紹三步列表法（如表2）：先假設雞有1只，再假設雞有2只，從中發現規律“每增加一只雞，減少一只兔，腿數會著減少2條。而76比54多了22條腿，所以要增加11只雞”。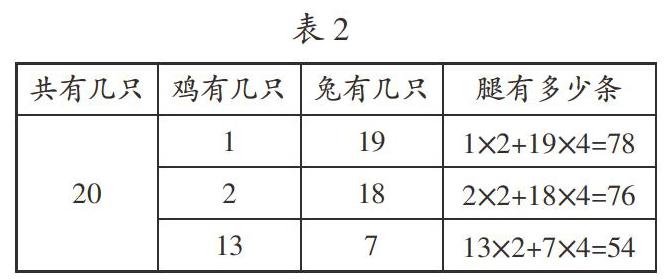

分析這幾種列表方式，發現它們的思維含金量是不一樣的。逐一列表法是學生一個一個去嘗試，學生有沒有根據前一次猜測的腿數對雞和兔的只數進行調整呢？我采訪過幾位學生，發現他們不是在調整，只是在一個一個地嘗試，進行地毯式的搜索，尋找答案；對于跳躍列表法，學生會根據腿數的多少進行調整，相差大，調整的幅度就大些，相差小，調整的幅度就小些，其思維含金量不言而喻——比逐一列表法要高；而取中列表法是學生對題中數據進行分析，再對答案進行估計：可能雞兔的只數相差不大，所以從中間開始猜測，再進行調整；最后一種是三步列表法，它要求學生利用“每增加一只雞，減少一只兔，腿數會著減少2只”這個規律，一步調整到位。

在分析學生可能出現的幾種思考方法后，我就可以做到有的放矢，由淺入深地組織學生學習。在組織交流逐一列表法時，我引導學生思考：“你是怎么猜測的？”重點觀察雞的只數、兔的只數及相應的腿數的變化規律。在組織交流跳躍列表法時，讓學生通過思考“腿數是多了還是少了”“說明了什么”“怎么調整”“為什么調整幅度這么大” “調整幅度怎么變小了”這幾個問題，進一步學習“調整”的策略。在組織交流“取中列表法”的過程中，學生就能感悟到：各種方法不是孤立的，要綜合運用，才能更快地解決問題。

三、辨析錯誤，矯正思維

一節課只有40分鐘，對于學生的一些錯誤，教師可以“放大”處理：拋出錯誤，讓學生在討論和爭辯中矯正思維，加深理解。在用列表法解決“雞兔同籠”問題時，如何根據已有猜測進行調整是教學難點，為了幫助學生把這個內容“踩實”，教師就要及時捕捉學生的錯誤，把其作為教學資源，引導學生在辨析錯誤的過程中鞏固正確認知。

有位學生給出了如表3所示的方法：在進行第二次猜測“雞有5只，兔有15只”時，他算出腿有70條，這70條說明腿多了。因此，在進行下一輪猜測時，就應該減少兔的只數，增加雞的只數，但這位學生還要增加兔的只數，顯然，他的調整是不恰當的。

我對這位學生的錯誤進行了放大處理。“70說明了什么？接著你又假設雞有4只，兔有16只，為什么這么調整？你是怎么想的？”這樣的問題，能讓學生深刻認識到：腿多了，說明兔多了，應該要增加雞的只數，減少兔的只數。

做教師要細心，做數學教師更要細心，要關注到學生解題背后的思考過程“這樣的思考過程對不對，這樣的思考過程是否簡潔”，只有深入分析學生的思考過程，才能糾正學生的錯誤，才能發展學生的思維。

四、建構模型，拓展思維

一節好的數學課應該讓學生懂得一個知識點，獲得一種思想，積累一類問題的學習經驗，形成簡單的數學模型，同時要讓學生在應用數學模型過程中，思維品質得到發展，思維能力得到拓展。在學生掌握了列表法之后，教師應從問題出發，提煉出“雞兔同籠”問題的基本模型，再帶領學生將這一簡單的數學模型應用到各種問題情境中，完成數學模型的建構與應用。

師：“雞兔同籠”問題是一個經典的數學問題。在日本也有此類問題的研究，日本人稱它為“龜鶴問題”。

師（出示龜鶴問題的圖片）：日本人說的“龜鶴”和我們說的“雞兔”有聯系嗎？

生1：有聯系，龜相當于兔，都是四條腿，鶴相當于雞，都是兩條腿。

師：像四條腿和兩條腿的，假如不叫它“雞兔同籠”，也不叫“龜鶴問題”，是否還可以取個其他名字？

生2：人狗問題。

生3：鴨貓問題。

……

師：看來，“雞兔同籠”可以換成烏龜和仙鶴，人和狗等問題，但歸根結底，它們也是“雞兔同籠”問題。其實“雞兔同籠”問題只是這一類問題的模型。在生活中也有許多類似于“雞兔同籠”的問題。

（1）三輪車和自行車共11輛，總共有25個輪子。三輪車和自行車各有多少輛？

（2）樂樂的儲蓄罐里有1角和5角的硬幣共27枚，總值5.1元，1角和5角的硬幣各有多少枚？

師：這些問題和“雞兔同籠”問題有關聯嗎？

生4：第（1）題里的自行車相當于2條腿的雞，三輪車相當3條腿的兔。

生5：第（2）題里的1角相當于雞，而5角就相當于兔，27枚相當于頭數，5.1元相當于腿數。

師：看來，在生活中有很多類似的問題都可以看成是“雞兔同籠”問題。

在這樣一個建構與應用中，學生明白了“雞兔同籠”問題只是一個簡單的“數學模型”，雖然問題的情境在變化，但問題的本質是沒有變，學生在解決這些問題的過程中逐漸形成“雞兔同籠”問題的解題思路和策略。

通過教學“雞兔同籠”這個內容，我深刻地認識到：教師要為學生的思維發展而教！數學教學是數學思維活動的教學，作為一名數學教師，要把握課堂的每一個細節，尋找行為背后的原因，思考結果背后的過程，為提升學生的思維能力而努力。當然，提高學生的思維能力是一個長期的過程，“冰凍三尺，非一日之寒”，如果能帶著“發展學生思維”的理念展開教學，相信我們的數學課堂一定會實現更大的效能！

（責編 金 鈴）