精心設計教學環節 循序滲透數學思想
馬天青
【摘 要】本文例舉數學課堂教學中滲透數學思想的基本方法與策略,提出要創設情境、滲透數學思想;設計問題、浸潤數學思想;小組合作、交流數學思想;教師引導、點撥數學思想;題組練習、運用數學思想;課堂小結、強化數學思想;單元復習、串聯數學思想;學業測評、提升數學思想;課外活動、延伸數學思想,以培養學生的數學思想方法,提高數學教學質量。
【關鍵詞】課堂教學 數學思想 創設情境 設計問題
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2018)03B-0112-03
數學思想是數學學科的精髓,它揭示數學的本質和發展規律,是解決數學問題的根本策略。《義務教育數學課程標準》明確指出:“數學思想蘊涵在數學知識的形成、發展和應用過程中,是數學知識和方法在更高層次上的抽象與概括,如抽象、分類、歸納、演繹、模型等。學生在積極參與教學活動的過程中,通過獨立思考、合作交流,逐步感悟數學思想。”這就要求教師全面挖掘、深刻分析、及時提煉數學思想,并在教學各個環節中循序滲透。
要在課前宏觀設計滲透數學思想的策略。數學思想隱含在數學知識中,與具體的數學知識結合成為有機整體,無法像數學知識那樣編為章節來教學。因此教師要總體把握每本教材、每個章節、每一節課中隱含的數學思想,宏觀設計滲透數學思想的框架,微觀擬定滲透數學思想的方案。在教案中必須寫出怎樣讓學生經歷知識的形成、發展、應用的過程,怎樣喚起學生深層次的數學思考,怎樣激發學生的學習興趣,怎樣切實可行地滲透數學思想等。老師成竹在胸,學生才會學有所獲。
要懂得課堂是滲透數學思想的主陣地。教師要精心設計教學環節,循序滲透數學思想,盡力打造高效課堂和智慧課堂。
一、創設情境,滲透數學思想
良好的開端是成功的一半,興趣是最好的老師。因此老師應該根據教學內容,創設恰當而豐富的教學情景,滲透數學思想,使學生興致勃勃地走進課堂。如人教版八下《17.1 勾股定理》的導入,我們組創設如下情境(見圖 1):
這是一個經典的滲透數學思想的情境,通過動人的故事、美麗的圖案和精彩的設計導入課題,巧妙滲透了觀察、抽象、猜想、數形結合、轉化、演繹等數學思想。數學教材中同類情境很多,都可以利用,充分發揮其作用。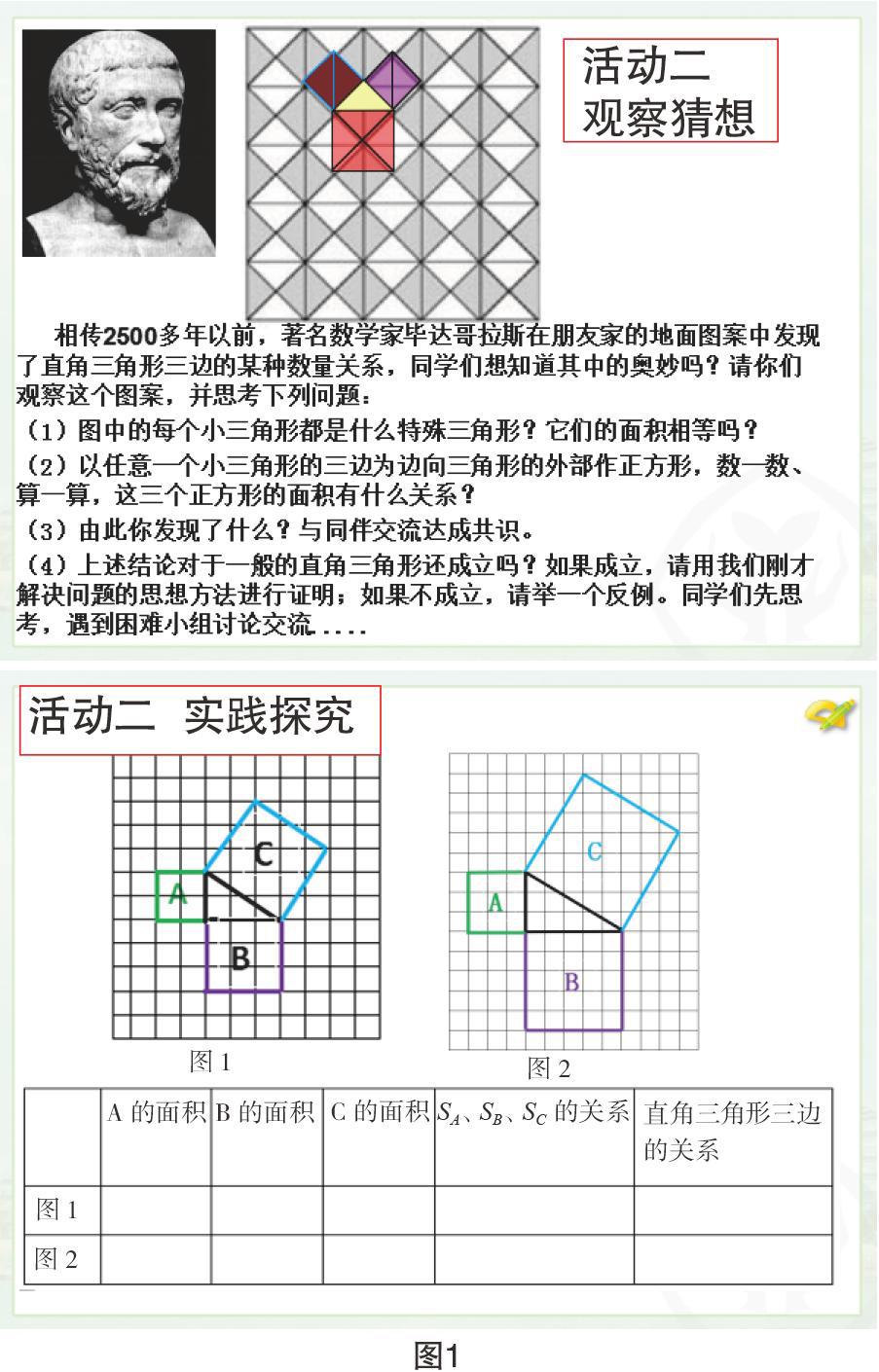
二、設計問題,浸潤數學思想
數學是大腦的體操,問題是數學的心臟。老師要善于在知識的關鍵點、障礙點、數學思想滲透點精心設計問題,并給學生足夠的時間思考,引導學生由淺入深地學習、思考、感悟數學思想。 如人教版七上《第 2 章 數學活動 3 》,筆者設計如下:
請同學們觀察手中的月歷(每個小組的月歷不同),并思考下列問題:
(1)橫排上的數字的排列規律。
(2)縱列上的數字的排列規律。
(3)對角線從上方到下方的數字排列規律。
(4)用矩形框住的四個數字的規律,你能用字母驗證這個規律嗎?
(5)將(4)中的某行數向右(左)移動一個數字的位置后,(4)中的規律成立嗎?為什么?
(6)用矩形框住月歷中的九個數字。
①這九個數字和與方框正中心的數有什么關系?
②將矩形移動幾個位置試試其中的關系還成立嗎?
③你能證明這個結論嗎?
(7)上述結論對于任何一個月的月歷都成立嗎?為什么?
三、小組合作,交流數學思想
在學生充分思考的基礎上,用小組競賽的方式鼓勵學生合作交流,大膽展示。尊重學生的個體差異和多樣化學習的需要,促使全班學生積極主動地、富有個性地學習。如,人教版九上《 24.1.1 圓》,筆者要求學生先預習、思考,再討論下列問題。
學生在思考、交流、展示的過程中掌握本節課必要的基礎知識與技能,感悟歸納、數形結合、類比、從特殊到一般、從一般到特殊的數學思想。
四、教師引導,點撥數學思想
對學生獨立思考、小組交流后存在的問題,老師要正確引導,巧妙點撥,熱情鼓勵。眾所周知,中考壓軸題知識點多、綜合性強、數學思想活,要引導學生攻克這一難關,教師必須認真研究全國各地近幾年的壓軸題,先按題型分類,同一題型從易到難排序;再對學生進行專項訓練、批閱、講評、糾錯、鞏固。如探究拋物線中特殊三角形的存在性就有:(1)直角頂點位置分類;(2)等腰三角形的兩腰分類;(3)全等(相似)三角形的對應元素的分類,等等。壓軸題的訓練與講解是點撥數學思想的好方法之一。
五、題組練習,運用數學思想
在挖掘本質的數學思想的基礎上,把課內外作業設計成梯度漸進的題組,有效訓練。講評時,教師不能只給答案,而要啟發學生:你是怎么想的?你為什么會這么想?同學們還有沒有別的解法?哪種方法更簡單?等等。如,學完九下《第 28 章 銳角三角函數》之后,筆者設計的題組如下(一組圖形,多種結論):
〖活動一〗畫圖說話
請同學們先在草稿本上畫一個 RtΔABC,∠C=90°,按下面要求寫結論。
(1)邊與邊的關系:
(2)角與角的關系:
(3)邊與角的關系:
(4)其他結論:
〖活動二〗添線識圖
請同學們畫出 RtΔABC 斜邊 AB 上的高 CD,并按要求寫結論。
(1)所有的直角:
(2)所有相等的銳角:
(3)所有的平方和等式:
(4)所有相似的三角形:
(5)所有的比例式:
(6)所有的等積式(包括射影定理):
〖活動三〗智力大比拼
(1)如果畫出 RtΔABC 外接圓 O,你又能寫出哪些新結論?
(2)如果把 RtΔABC 繞斜邊 AB 所在的直線旋轉一周,形成什么樣的幾何體?你能求出它的表面積嗎?相信你是最棒的。
(3)你還有什么新的發現?讓大家共享你的智慧。
六、課堂小結,強化數學思想
課堂小結引導學生反思和評價自己的學習情況,老師予以鼓勵,讓學生感受成功的喜悅。同時老師還要強化本節課的數學思想,并為下一次課設下懸念,激勵學生課外繼續探討。如,人教版七上《 3.1.1 一元一次方程》(第 1 課時)的小結,我們組設計如下:
又如,人教版八下《17.1 勾股定理》(第 1 課時)的小結,我們組這樣設計:
七、單元復習,串聯數學思想
在復習梳理知識點的同時,還要對數學思想進行串聯,使學生進一步領悟數學思想的價值,實現質的“飛躍”。如人教版八上第 13 章第 3 單元《等腰三角形》復習,我們組設計為:
先回顧等腰三角形的定義、性質和判定,然后設計練習,對數學思想的應用進行串聯和總結。
1.第一類題目:分類討論
(1)等腰三角形的兩條邊的長分別是 5 和 8,則它的周長為 ;若兩邊長分別為 3 和 8 ,則它的周長為 。
(2)已知等腰三角形一個角為 50°,則底角的度數為 ;若這個角為 100°,則底角的度數為 。
(3)等腰 △ABC 一腰上的高與另一腰的夾角為 30°,則頂角的度數為( )
A.60° B.120° C.60°或 150° D.60°或 120°
教師引導學生小結:
在解與等腰三角形相關的題目時,經常會運用分類思想進行討論。
等腰三角形的邊不確定→分類(滿足三邊關系)。
等腰三角形的角不確定→分類(滿足三角形的內角和定理)。
2.第二類題目:方程思想
(1)如下左圖,在 △ABC 中,AB=AC,AD=BD=BC,求∠A 的度數。
(2)如下右圖,∠DEF=36°,AB=BC=CD=DE=EF,求∠A 的度數。
(教師引導學生小結:這兩個題如果把∠A 的度數設為 x,列方程解答可以化繁為簡,體現方程思想在幾何計算題中的應用)
3.第三類題目:轉化思想
一 變式二
變式三 變式四
已知,如上左圖,AB=AC,BD 平分∠ABC,CD 平分∠ACB。問:圖中有幾個等腰三角形?
變式一:若將題中 △ABC 改為一般的三角形,其他條件不變。問:線段 EF 與 BE、CF 有何數量關系?
變式二:若過 D 作 EF∥BC 交 AB 于 E,交 AC 于 F,則圖中增加了幾個等腰三角形?
變式三:將 CD 變成 △ABC 的外角 ∠ACG 的平分線,其他條件不變。EF 與 BE、CF 之間有什么數量關系?
變式四:BD、CD 為 △ABC 兩外角 ∠CBM、∠BCN 的平分線,其他條件不變。EF 與 BE、CF 之間有什么數量關系?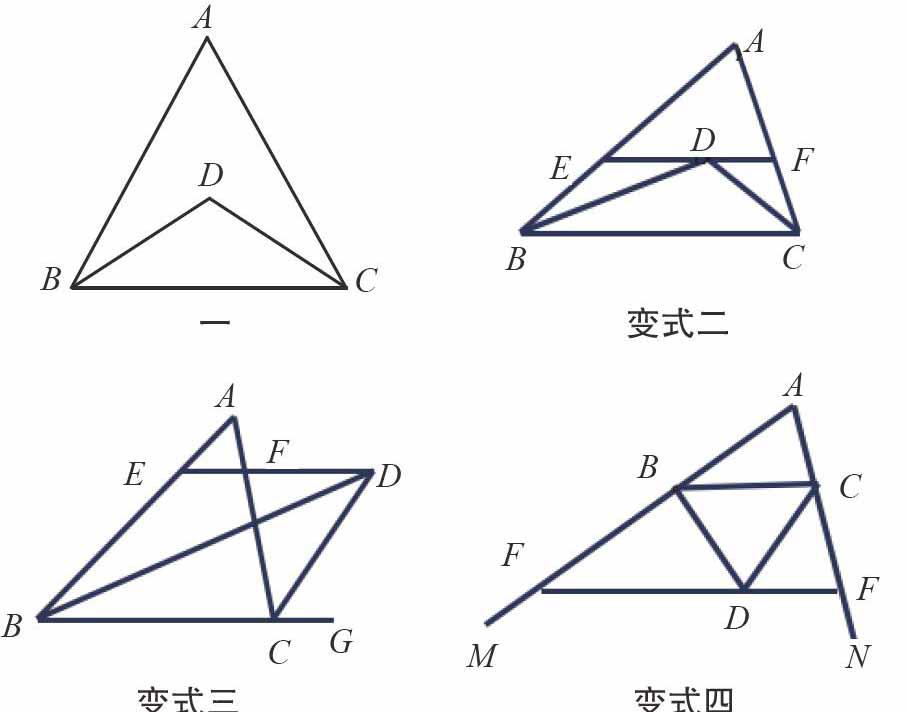
教師引導學生小結:
角與角的轉化→相等角之間的代換。
邊與角的轉化→在同一個三角形中等邊對等角,在同一個三角形中等角對等邊。
邊與邊的轉化→相等線段之間進行代換。
八、學業測評,提升數學思想
教師命題時,要重視數學思想的測評點。提倡教師引導學生自主命題,按“個人選題—小組篩選整合—老師挑選試卷測評—師生共同分析利弊—命題者修改完善”的程序循環進行,如此這般,學生對數學思想的理解自然而然得到提升。
九、課外活動,延伸數學思想
課外活動是課堂教學的補充,教師應該組織學生參加一題多解、專題講座、智力競賽、編手抄報、制作模型、統計調查等活動,讓學生在活動中延伸數學思想。
數學是思維的種子,是培養學生“會思想”的載體,教師要善于引導學生用數學思想和方法建構知識體系,使數學思想內化為學生的數學素養。
【基金項目】教育部中國智慧教育督導“十三五”科研規劃重點課題“教育模式創新的研究與實踐”之子課題“初中數學課堂教學中滲透數學思想的策略與方法”(EDUZHI 30041-KYKT1468)。
(責編 盧建龍)

