小學數學教學中轉化思想的運用
曹曉偉
[摘 要]在小學數學教學中轉化思想具有非常重要的指導意義,是學生解答數學問 題的有效方法。因此,在小學數學教學中,教師應全面了解轉化思想的內涵與重要 性,并恰當地將其滲透到日常的課堂活動中,引導學生將抽象復雜的數學問題進行 轉化。本文以提高小學數學教學質量為目的,通過對轉化思想的分析,探究其在小 學數學教學中的運用。
[關鍵詞]小學數學; 轉化思想; 運用策略
轉化是數學教學中最常用最基本的思想方法之一,轉化就是對于某些直接求 解比較困難的問題,通過觀察、分析、類比、 聯想等思維過程,選擇運用恰當 的數學方法進行轉化變換,將原問題轉化為一個已掌握的比較容易的問題,通過 對轉化出來的問題的求解,達到解決原問題的目的,轉化是一種十分有效的思想 方法,是數學思想的核心和精髓部分,是數學思想的靈魂所在。因此,教師應把 這種思想體現在教學的每一個環節中,讓學生更輕松更高效的學習。
一、運用類比,實現轉化
當一個比較陌生或復雜的問題與一個比較熟悉或簡單的問題之間具有某種 相似性的時候,可以把解決前者所用的方法加以推廣應用到后者,這種思想方法 叫做類比。因此,在學習數學新知識時,適時運用類比方法進行轉化,可使陌生 的問題轉化為熟悉的問題,有利于學生更好地接受新知識,鞏固舊知識。 例如:在教學“圓的面積公式”時,可讓學生先把一個圓若干等分,然后把 它拼成一個近似的長方形,思考:長方形的長和圓的周長有什么關系,寬和圓的 半徑有什么關系,學生通過觀察比較分析得出:長方形的面積就是圓的面積,長 方形的長就是圓的周長的一半,長方形的寬就是圓的半徑,從而得出了圓的面積 公式,這樣通過類比的方法將新知識轉化為已經學過的知識,學生輕而易舉的掌握了圓的面積公式的推導過程,并牢記了圓的面積公式,可見運用類比方 法實現轉化是數學學習的一種有效途徑。
二、數形結合,實現轉化
數形結合的思想是充分利用“形”,把一定的數量關系形象地展示出來。即 通過作一些如線段圖、面積圖、集合圖等來幫助學生正確理解數量關系,使問題 的內容具體化、形象化,從而把復雜問題轉化成簡單的問題。
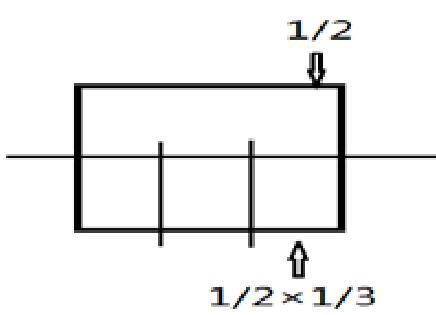
例如:在教學“分數乘法時”時,算:1/2×1/3= 1/6 ,如果想讓學生充分理解算法, 可以采用畫圖法(如下圖所示),我們可以通過這樣的數形結合的轉換得到結果。 可見,數形結合是實現新舊知識轉化的重要方式,通過畫圖形來進行轉化,可以 加深學生對知識的理解,培養學習數學的興趣。
三、條件替換,實現轉化
條件替換是數學學習的重要方法。替換的實質是改變題目的形式但卻不改變 題目的本質。當我們遇到題意比較難懂的習題時,可以把題中的某一個條件或問 題替換成與其內容等價的另一種表達形式,這樣解題思路就會變得明朗起來,有 山重水復疑無路,柳暗花明又一村的感覺。 例如有這樣一題:1 只鵝=2 只雞,1 只羊=4 只鵝,1 只羊+1 只雞=18 千克。 求一只雞、一只鵝、一只羊各多少千克?解題思路是用替換轉化法:把算式 1 只羊+1 只雞=18 千克中的 1 只羊替換成 4 只鵝,4 只鵝再替換 8 只雞,這樣就看 出 9 只雞=18 千克,從而得出 1 只雞=2 千克,1 只鵝=4 千克,1 只羊=16 千克。 在整個解題過程中,學生通過兩次替換的方法,將未知的問題轉化為已知條件, 從而求出題中雞、鵝、羊的質量。可見,當遇到一些問題不能直接解決時,我們 可以用替換的策略進行解題思路的轉化。
四、統一條件,實現轉化
統一條件就是通過協調問題中沒有統一的部分,來找出條件之間的本質聯 系,便于解題。如在解答較復雜的分數應用題時關鍵是把握單位“1”,單位“1” 是可以轉化的。根據分率的意義,有時只要換一個角度去看,將已知分率加以適 當調整,分率所從屬的單位“1”就可以完成轉化,實現了統一單位“1”的目的, 從而使條件得到統一,使題目的解答變得非常簡便。
五、運用假設法,實現轉化
在小學數學中,學生對思考性較強的問題常常感到難以解決。因此,教師在 教學過程中要注意教給學生解決問題的方法,以提高他們的思維能力。而假設方 法往往在解決問題的過程中起關鍵性的作用。假設法就是把抽象性的問題轉化為 比較具體的問題,使其中的數量關系更加明確,解題方法學生比較容易接受。 例如:在解決“一個數減少 20%后又增 加 20%,結果是原數的百分之幾?” 這道習題時,學生一開始顯得束手無策,若引導學生運用假設法進行轉化,問題 就迎刃而解了。這里可將這個問題具體化,如設這個數是 100,100×(1-20%) ×(1+20%)=96,結果是原數的 96%。可見,假設法是一種常用的數學轉化策 略,在解題過程中引導學生合理、靈活地運用它,可使復雜問題簡單化、具體化。
以上是我總結的幾種教學上常用的“轉化”的思維方法,不同的問題采用不同 的轉化方法,可以化難為易,使學生加深新舊知識之間的聯系,容易接受及內化, 效果顯著。
六、結語
教師在教學活動中要通過從轉化的角度去把握教材,只有對教材內容的相互 聯系分析得比較透徹,才能更好地把握教材的整體性、結構性。這樣在備課和教 學中才能居高臨下,有的放矢地進行教學。學生在感知、體驗轉化方法的過程中, 對數學知識之間的聯系也能認識得更深刻。同時也有利于學生對數學知識結構的 構建和形成。數學教學中轉化的思維方法的形成不是一朝一夕的事,必須循序漸 進的反復訓練,因此教師應在不同內容的教學中不斷地進行學習、進行嘗試、進 行總結,從而提高自身的教育教學能力。

