在數學課堂教學中融入數學文化淺探
龍振業
【摘要】本文結合教學案例論述教師在數學課堂教學中融入數學文化的策略與意義:吸引學生的注意力,幫助學生理解抽象的概念與定理等;運用數學文化將各個知識點串聯成系統的知識體系,減輕學生的學習負擔;探究數學文化中蘊含的數學思想,提升學生數學素養。
【關鍵詞】數學文化 知識體系 數學思想
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2018)01A-0133-02
一、滲透數學文化,理解數學知識
數學是一門與概念、定理、公式相關的學科,教師在數學教學中滲透數學文化、設置與教學內容相關的且蘊含在現實生活中的數學文化、引導學生思考其中所隱含的數學知識和規律,對學生的數學學習具有巨大的幫助。
(一)理解概念
數學源自生活,數學的概念也是對生活的抽象延伸。教師可以在概念教學中融入數學文化,將數學與生活聯系在一起、將枯燥的概念教學趣味化,讓學生感受到數學與生活息息相關,學會運用數學文化理解概念。
例如,在學習蘇教版數學七年級上冊《整數和負數》時,“負數”概念對學生來說相對抽象但并不陌生,同時學生對溫度計已有一定的認知。教師在教學時可以將溫度計和海拔高度作為教學起點,讓學生感受正、負數的實際意義,理解負數概念,建立正、負數的數感。教師也可以在教學中滲透數學文化史:中國是最早提出負數的國家,《九章算術》是最早、最完整介紹負數的古算書,人們在求解方程時經常會遇到小數減大數的情形,為便于求解,便創造了負數;在古代為區分正負數,數學家創造了一種方法:用不同顏色的算籌來表示正、負數;中國古代不僅提出了負數的概念,還提出了整套的正、負數的運算法則,這些法則沿用至今。教師在教學中融入數學文化,讓學生了解概念產生的背景和意義,利用概念與生活的相通性可以幫助學生更直觀地理解概念。
(二)理解定理
初中學生的數學認知處于發展階段,定理教學要避免追求進度而忽視讓學生體驗探究過程。為了幫助學生理解定理,教師可在教學中引入數學文化,通過多樣的活動使學生對定理逐漸形成自我感悟,從而理解定理,同時讓學生的思維經歷完整的探究過程,學生在獲得知識的同時,得到思維、情感的多重發展。
例如,教師在教學蘇教版數學八年級上冊《勾股定理》時,可以從畢達哥拉斯到朋友家做客的故事入手:畢達哥拉斯是古希臘最為著名的數學家之一,相傳2500年前,他到朋友家做客,發現朋友家用地板磚鋪成的地面反映出了直角三角形的三邊關系。畢達哥拉斯發現直角三角形的三邊關系的故事為《勾股定理》的教學提供了問題引入,學生通過思考故事中隱含的規律,從而進行猜想假設,再加上教師的演示將定理變得具體形象,學生能夠更容易地總結出直角三角形的三邊關系,即勾股定理。探究勾股定理相關的數學文化史的過程蘊含了豐富的數學思想方法,這對學生理解定理極為有利。
將數學文化滲透到數學教學中,將教材內容與數學文化巧妙結合起來,從數學文化中延伸出數學概念和規律,可以幫助學生理解相關內容。數學文化中蘊含的故事具有較強的趣味性,還可以激發學生的學習興趣。
二、編排數學文化,構建知識體系
隨著學習的深入,初中數學的知識點增多,如果教師按照傳統的教學方式將知識點分開進行獨立教學,勢必會增加學生的學習負擔,同時也難以保障學習質量。教師在教學中可以以數學文化為主線,將零碎的數學知識點通過主線串連起來,幫助學生構建知識體系,這對學生開展系統學習、整體把握知識極為有利。
例如,當學生依次學習了自然數、整數、有理數、無理數等知識點后,教師可以講述這些知識點在數學史上出現的背景,從而將這些內容串聯起來:在人類最初的生產生活中,為了表示所獲得物品的數量,創造出了自然數的概念;隨著對物品的分配使用,人們需要對其進行分割,就出現了分數的概念;再后來,為表示具有兩個相反意義的數量,人們引入了正負數的概念;為了使度量的量是連續的,人們創造出了無理數……這樣以數學文化史為線索的敘述方式,自然而然地將各個知識點串聯起來,形成完整的、系統的知識體系。
數學的發展史就是一段數學文化史,這也是數學知識的發展特征,這一鮮明特征能夠滿足我們將初中數學知識點串連起來的需求,教師通過陳述數學文化史的方式將知識點進行系統整合,調動學生的學習興趣,讓學生在聆聽文化史時對知識形成深度認識、構建知識體系,這樣的教學方式可以達到事半功倍的效果。
三、提煉數學文化,凝聚數學思想
對數學文化的認知不能只停留在知識提取的初始階段,教師要引導學生對數學文化產生認同感,從中凝練出數學思想,使學生真正有所收獲,提升數學文化素養。數學文化中蘊含有數形結合思想、化歸統一思想以及分類討論思想等,教師要適時地對這些數學思想進行解釋、總結,發展學生的數學思想,讓學生理解每一個故事背后都蘊含著規律的推演求證,從而獲得數學學習的樂趣。
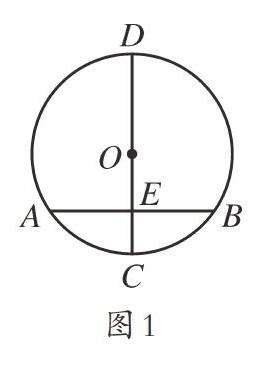
例如數學巨著《九章算術》中有一個關于“圓材埋壁”的問題:今有圓材,埋在壁中,不知大小,以鋸鋸之,深一寸,鋸道長一尺,問徑幾何。“翻譯”為現在的數學題,大意為:如圖1,CD為⊙O的直徑,弦AB⊥CD,垂足為E,已知CE=1,AB=10,求圖中CD的長度。
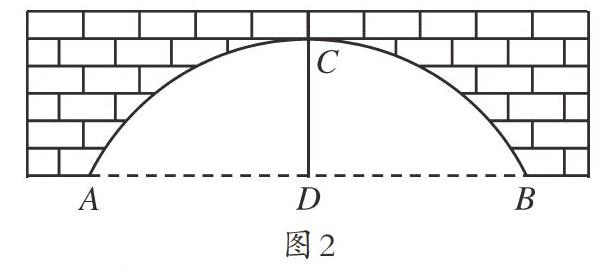
面對這樣的練習題,教師可以根據題意啟發學生運用垂徑定理和勾股定理來求解,更重要的是引導學生去探究故事中蘊含的數學思想,感受其中有關數學建模的價值。基于建模思想,教師可以對此題進行拓展延伸:如圖2所示的圓弧拱橋,跨度為60米,拱橋高18米,水文測算,當洪峰通過跨度小于30米時,需要采取緊急措施,問:拱頂離水面4米高時,是否需要采取緊急措施?在數學文化背景下,引導學生感知建模思想和數形結合的思想,可以有效地幫助學生解決問題。
上述例子中,教師通過練習引導學生提煉出建模思想,建模思想是對事物或現象所包含的數量關系以及位置關系的高度概括和形象描述的思想方法。數學文化中所蘊含的思想方法對學生數學思維提升具有指導意義,教師合理地運用數學文化隱含的思想方法,可以使學生形成運用數學思想的意識,促進學生高效解題。
總之,數學文化對初中數學的學習具有十分重要的意義,教師在教學中滲透數學文化,可以幫助學生理解數學知識;在知識點的編排中融入數學文化史,可以有效構建知識體系;通過提煉數學文化,可以歸納出數學思想。數學文化融入數學教學,不僅有助于學生理解知識,還可以開闊學生視野,提升學生的數學素養。
(責編 劉小瑗)

