高中數學推理與證明中的“偽證”思想

鄧正南

摘要：本文以“偽證”思想為切入點，就其概念含義做分析探討，并就其在高中數學推理與證明教育中的作用方式與教學實例做細致的闡述研究，期望為高中學生數學推理意識與證明能力的培養提舟提供有益的參考。

關鍵詞：高中數學 推理 證明 “偽證”思想

證明與推理是數學學習中最為基礎與重要的思維步驟，也是高中學生數學學習中重要的思考方式，作為高中數學教學中至關重要的內容之一，對學生推理與證明意識的培養一直是教師的重點教育研究對象?；诖斯P者認為將“偽證”思想應用進高中數學推理與證明教學進程中，將有助于提升課堂教育質量，并推動學生推理意識與證明能力的發展。因此筆者以“偽證”思想為研究出發點，就其理論相關含義知識做闡述分析，并對其在高中數學推理與證明中具體教學應用方式做詳細的探討研究。

一、“偽證”思想概述

“偽證”思想即偽證主義科學觀，其理論來源于英國學者波普爾的著作《猜想與反駁》，該觀點是基于對邏輯實證主義的反駁，由波普爾提出的對偶然真理界定的偽證主義。其理論思想的證明方式采用試錯法，即不斷對科學問題提出各類假說與猜測，之后思考與找尋符合其假說猜測的事例，然后依照已有事例對原本的假說猜測予以修正，并不斷循環重復這一證明過程，最終將原本提出的猜想假說予以否決，以驗證與完善科學理論觀點。

二、高中數學推理與證明中利用“偽證”思想進行教學的研究

為具體研究“偽證”思想在高中數學推理與證明中的教學應用，筆者以概率這一高中數學中的重要知識概念為切人點，就“偽證”思想在概率知識教學中的策略與方法做研究分析。

學生在初中階段已對概率知識有了初步的了解與認知，但因其本身知識概念的抽象性，在高中數學教學中依然是學生較難以領會與掌握的難點內容之一。同時學生在學習過程中的各個階段環節都容易出現各類理解偏差與錯誤，進而生成錯誤的知識概念。而相應的概念認識一旦形成，要進行消除與糾正就會十分困難。正因為概率這一知識內容的特性，將“偽證”思想應用進其教學活動中，有利于促進學生對概率知識的理解認知深度，并提升其數學推理與證明能力。因此筆者以概率知識的課堂教學相關實例，探究具體的“偽證”思想應用方法。

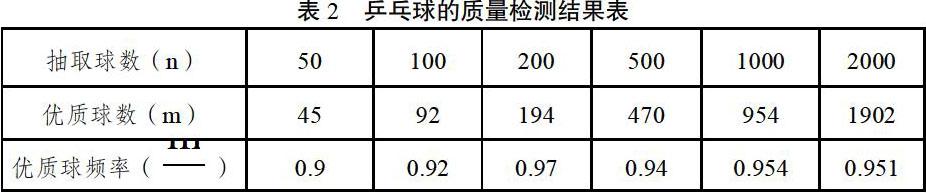
例如在教授概率內容時，教師可先為學生提供相應的隨機事件數據表格，來讓學生思考并分組探討如何基于隨機事件的頻率，推定其具體的概率數值。隨機事件頻率表如表1、2所示。

在學生合作討論之后選取各組代表做意見表達，學生能得出表1中所有向上頻率的平均值為0.5046，其與生活中的實踐經驗是相同的，表2的數據學生雖然缺乏相應的檢驗經驗，依然能取其平均值作為概率。此時教師可為學生提出新的思考方向：雖然表1所得的結果的確如此，但其是否真的能作為一個普遍性結論，應用到各類隨機事件的推理過程嗎？以引導學生向對概率平均值計算的“偽證”方向予以思考。在學生相互探討后再次請各組代表發言，有做積極思考的小組就能發現表2所有概率的平均值是0.9392，但其頻率數值明顯帶有向0.95變動的趨勢，因為伴隨實驗次數的增大，頻率的平均值應該更接近于概率才對。因此對表2的概率值計算應取其最大次數下的頻率數值做平均計算，將大實驗次數下的平均值作為隨機事件的概率值。

對這種觀點教師可再引導學生向完全證明其猜想的科學性出發，對取較大試驗次數下平均值的推測做偽證推理，以啟發學生向“足夠大”這一概念定義產生疑問與思考，并進一步推論所示所選取的試驗次數不同，那所得出的頻率平均值也會不同，因此對概率值的測算不能僅適用“較大”的試驗次數這一模糊概念，因為近似值往往不是唯一的，模糊范圍下產生的概率數值也會不精確。之后可總結出在海量試驗下，隨機事件A的產生會呈現相應的規律性。在試驗次數次數n→+∞時，發生概率m/n總是趨于接近的常數就是其概率，相應表達式可概括為對數列（m/n）來說，P （A） =lim m/n。

n→∞

但此觀點依然不夠深入與全面，在此基礎上教師可為學生溫習極限的概念，引導學生對該表達式做進一步的思考，最終由部分學優生發現其問題所在：在數列極限概念中，對任意的ε >0，則總是存在一個正整數N，且當n>N時，|a_n-A|<ε，此時常數A是數列{a_n）的極限，因此對于數列（m/n），其概率值雖然總是在某一個常數周圍變動，但并不總能確保其概率值總是趨近于這個常數，還是會有反復現象的出現，因而不能將發生頻率接近的常數作為表2的概率值。

三、結束語

從以上概率知識的教學實例可發現，基于偽證思想應用進高中數學教育中，能有效促進學生對知識概念的反復理解與探究，在不斷的“偽證”進程中充分理解與把握所學知識的內涵與深意，使其有效掌握到高中數學中較為復雜與抽象的理論知識。

參考文獻

[1]包曉兵.“證偽”思想在高中數學教學中的作用[J].理科考試研究，2015，23： 30.

[2]劉長柏.數學思想在《推理與證明》中的運用[J].中學生數理化（高二），2016.02：12-13.