“三招”助力數學總復習教學

韋茂林

[摘 要]以往的數學復習課一般都是由教師引導學生回顧總結舊知，然后通過“題海戰術”進行鞏固和深化。隨著課程改革的深入實施，復習課教學，教師應引導學生構建精密的知識網絡：縮小看，纖毫畢現，細致入微；放大看，全貌全局，一覽無余。

[關鍵詞]小學數學；總復習；查漏補缺；交流優化；意義遷移

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2018）33-0029-01

復習課上，如果教師只是抽取知識點，讓學生被動識記的話，那這樣的識記是模糊的，甚至可能是錯漏百出的。學生不需要這樣生硬的“鋼結構”，而要具有生長力和智能型的“集成電路”。

一、查漏補缺，問題引導，搭建框架

復習不一定要放在學習所有的新知之后，而應趁熱打鐵，立即進行回憶、梳理，因為及時地查漏補缺不僅能為后面學生的分享交流提供依據，而且可以提高復習課的教學效率。

例如，復習“數的認識”之前，教師先讓學生回顧所有學過的數集：（1）數的種類很多，有無數個；（2）數有正負數、奇偶數、合數與質數、分數、整數、小數之分；（3）正數前面可省去“+”號，負數一定要帶“-”號；（4）質數除了1和它本身外沒有其他的因數，合數反之；（5）偶數都可以被2整除，奇數則不行；（6）分數既可以表示具體數量，又可以表示比例；（7）小數和分數可以互化。這是學生自己的復習總結，都是提綱條文，從中可以發現學生腦海中的知識點是分散的，每個新知的出現沒有建立在舊知的基礎上，所以各知識點的層次、從屬關系混亂。于是，教師以問題為導向，進行搭建框架的教學設計。

師：在復習“數的認識”之前，我們先梳理一下以下幾個問題：我們學過的數有哪些？它們之間的關系是什么？如何分類？想辦法把這些內容繪制成圖譜。

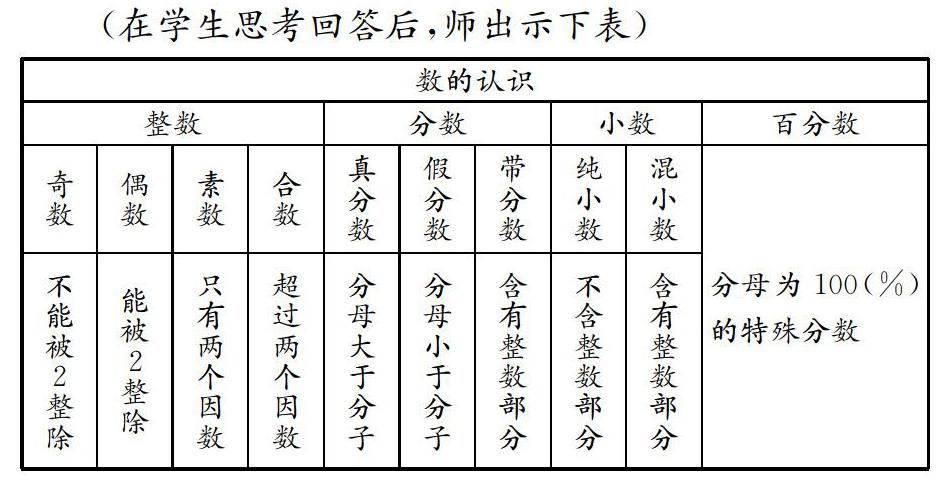
（在學生思考回答后，師出示下表）

……

上表展現了知識間的內在聯系，使學生真正理解和掌握各個知識點，為后期的交流探討打下基礎。

二、交流優化，深度梳理，內化吸收

復習課上，學生的交流分為兩個層次：第一層次，教師引領學生構圖，感受構建知識框架的優越性；第二層次，提煉方法，讓學生體會到繪制知識圖譜需要掌握全部的知識點。

例如，復習“數的認識”這一單元時，教師以數軸為主線貫穿教學始終：“請在數軸上表示出3、0.30、-3、6這幾個數。”學生要在數軸上表示出這幾個不同形態的數，首先要確定“1”的位置，也就是規劃出單位“1”的長度。如對0.30的定位需要借助分數的意義，即將一個基本長度單位劃分為10份，取其中的3份；對于3與-3的定位，則需要借助數軸的方向性與正負號的指代意義。同時，教師還可以指導學生總結經驗，收集經典例題，使學生在命題、做題、評題的過程中學會從命題者的視角去理解和掌握所學知識。

三、意義遷移，整合統一，凸顯思想

復習課上，教師在引導學生構建知識框架時，既要達到全面、深入、詳細的要求，又要巧妙地整合提煉，做到厚積薄發。如對“能簡便計算要用簡便方法計算”這類題的復習，教師可先引導學生整理出所有的運算律，再尋找其中的相通之處，最后通過整合，使學生高效地掌握所學知識。

關于分配律，既可以是乘法對加數進行分配，又可以是乘法對被減數和減數進行分配，表達式為（a+b）×c=a×c+b×c、（a-b）×c=a×c-b×c，理解為“合并后再擴大相同倍數，可以先擴大相同倍數再合并”。細想減法的性質和除法的性質，表達式為a-b-c=a-（b+c）、a÷b÷c=a÷（b×c），可以類似地解釋為“分批分次減去（除去）兩個數，可以集中一次性去除”，也可以看成為減法和除法的特殊結合律。

交換律同樣可以遷移到減法、除法中，表達式為a-b-c=a-c-b、a÷b÷c=a÷c÷b。教師可讓學生先發現連減、連除算式中交換減數和除數的位置后得數不變，再應用逆運算概念，轉變為負數、倒數的概念。交換減數和除數的位置，實際上就是加法交換律和乘法交換律的翻版，即a-b-c=a-c-b與a+（-b）+（-c）等價，而a+（-b）+（-c）=a+（-c）+（-b）。同理可知，a÷b÷c=a×1b×1c=a×1c×1b=a÷c÷b，這里可以看成為減法和除法的特殊交換律。

經過運算意義的貫通整合，各種紛雜的運算律就可以統一起來：在只含同一級的混合運算中，均存在交換結合定律；在含有兩級的混合運算中都存在分配現象，即二級運算分配給一級運算。

總之，在將舊知梳理、融會貫通時，更需提煉出更為宏觀的概念——數學思想、數學學習的策略方法，使學生能從更高的層面上掌握所學知識。

（責編 杜 華）