根據學生的想法推進教學

【摘要】本文結合蘇教版數學六年級上冊《解決問題的策略——假設》教學過程，論述教師站在學生的角度設計教學、推進教學的途徑，認為教師應以學生為本，注重新舊知識之間的聯系。

【關鍵詞】小學數學 以生為本 假設 方程

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2019）11A-0139-02

假設策略是解決問題時常用的策略，學習此策略不但有利于學生數學活動經驗的積累，同時對提高學生提出問題、解決問題的能力都有著重要的意義。運用假設策略解決問題是蘇教版數學六年級上冊第四單元的內容，是問題解決過程中常用的策略，對學生分析實際問題的數量關系，積累解決問題的經驗，感悟一些基本的數學思想方法，提高分析和解決問題的能力等，都有著重要的意義。

假設策略的學習是在畫圖、列表、列舉、轉化等策略的基礎上進行的，雖然學生在生活中或以前的學習中接觸過假設策略，如計算除數是兩位數的除法，把除數當作整十數試商等，但是他們缺乏有序、有效的思考，沒有形成策略意識。經歷運用假設策略解決實際問題的過程，從而“悟”出假設策略，形成策略意識恰恰是解決問題的關鍵。

一、教學前測

引導學生自然地悟出假設策略，體會假設策略的優勢是有些挑戰的。于是筆者在教學設計之前進行了教學前測：“小明把720毫升果汁倒入6個小杯和1大杯，正好都倒滿。已知大杯的容量是小杯的3倍，小杯和大杯的容量各是多少毫升？”多數學生選擇列方程解答，少數學生將6個小杯假設成2個大杯，或將1個大杯假設成3個小杯，還有個別學生無法解答。教師在設計教學時應站在學生的立場，提出以下幾個問題：為什么要選擇假設的策略解決問題？可不可以運用列方程的方法解決？兩種方法之間有什么聯系與區別？帶著這些問題，筆者設計教學時進行了一些思考。

二、案例描述

片段一：對比復習，為認識假設策略鋪墊

教師通過課件出示準備題：

（1）小明把720毫升的果汁倒入6個小杯中，正好都倒滿，每個小杯的容量是多少毫升？

（2）小明把720毫升的果汁倒入3個大杯中，正好都倒滿，每個大杯的容量是多少毫升？

教師在學生回答的基礎上總結：剛剛這兩題都是比較簡單的實際問題。

片段二：自主探究，體會假設策略的優勢

（教師出示例題：小明把720毫升的果汁倒入6個小杯和1個大杯，正好都倒滿，小杯容量是大杯容量的[13]，小杯和大杯的容量各是多少毫升？）

師：誰來說說這里有哪些已知條件？你打算怎樣解決？

生1：我打算用方程解決，設小杯的容量為未知數x，那大杯的容量就是3x，列出的方程是6x+3x=720。

生2：也可以畫圖試一試。

……

師（過渡）：是的，這里數量關系較為復雜，選擇你喜歡的方法試著解答，再和小組成員說一說。

（學生板書，小組匯報）

生1：我是列方程解決的，設小杯的容量為x，方程就是6x+3x=720，解出小杯的容量是80毫升，大杯的容量是240毫升。

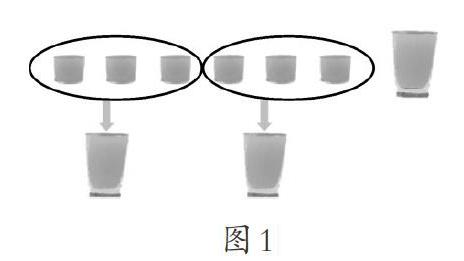
生2：我是畫圖來解決的（如圖1），將6個小杯換成2個大杯，那么720毫升果汁正好倒滿3個大杯，每個大杯的容量就是720÷3=240（毫升），每個小杯的容量就是240÷3=80（毫升）。

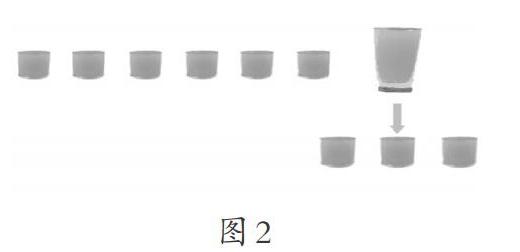
生3：我也是畫圖來解決的（如圖2），將1個大杯換成3個小杯，那么720毫升果汁正好倒滿9個小杯，每個小杯的容量就是720÷9=80（毫升），每個大杯的容量就是80×3=240（毫升）。

師（課件出示兩幅圖并提問）：請同學們比較全部倒入大杯和全部倒入小杯這兩種方法，它們有什么相同點、有什么不同點？

師（總結）：相同點有果汁總量不變，都是720毫升，都是將有兩個未知量的問題假設成只有一個未知量的問題;不同點是一種方法是將大杯假設成小杯，一種方法是將小杯假設成大杯。

（教師板書：兩個未知量假設成一個未知量

大→小

小→大）

師（引導學生檢驗）：這樣列式解答的結果一定正確嗎？還需要怎么辦？我們既要看小杯的容量是不是大杯的[13]，又要看6個小杯和1個大杯的容量和是不是等于720毫升。

師：剛剛同學們有的是列方程解決問題，有的是運用假設的策略列式解決問題，你喜歡哪種方法呢？為什么？

生1：我喜歡將2種杯子假設成1種杯子，這樣簡單，列方程比較麻煩。

生2：我喜歡方程，數量關系更直接。

……

師（總結）：同學們都很有想法，看來列方程或者通過假設來解決這個問題各有各的優點。

片段三：感悟比較，發現假設策略的局限性

師（課件出示）：小明把720毫升的果汁倒入6個小杯和1個大杯，正好都倒滿，小杯容量是大杯容量的[23]，小杯和大杯的容量各是多少毫升？

生1：可以設大杯的容量為x，小杯容量就是[23]x，方程就是x+6×[23]x=720，解出小杯的容量是96毫升，大杯的容量是144毫升。

生2：我覺得這樣的小杯也可以假設成大杯，但是有點困難。

師：有同學知道嗎？

生3：小杯容量是大杯容量的[23]，也就是1個大杯可以看作3份，一個小杯就可以看作其中的2份，6個小杯就有12份，12÷3=4（個），那么720毫升果汁正好倒滿5個大杯，每個大杯的容量就是720÷5=144（毫升），每個小杯的容量就是144×[23]=96（毫升）。

生4：也就是1個大杯被平均分成3份，其中的2份看作1個小杯的容量，一份看作小杯容量的一半，那么720毫升果汁正好倒滿7.5個小杯，每個小杯的容量就是720÷7.5=96（毫升），每個大杯的容量就是96×1.5=144（毫升）。

師：這時候對于列方程和假設策略，你有什么想說的？

生1：假設策略理解起來很復雜，方程很好理解，比較簡單，我喜歡列方程解題。

生2：當小杯容量是大杯容量的幾分之一時，假設策略更方便。方程沒有什么局限性，就是過程麻煩點。

三、案例反思

（一）關注新舊知識間的聯系

在導入環節，教師通過復習含有一種未知量的兩個簡單問題：（1）小明把720毫升的果汁倒入6個小杯中，正好都倒滿，每個小杯的容量是多少毫升？（2）小明把720毫升的果汁倒入3個大杯中，正好都倒滿，每個大杯的容量是多少毫升？溝通新舊知識之間的聯系，既為學習含兩種未知量的問題鋪墊，又激發學生的學習興趣，使其產生新的學習需求。

（二）關注學生視角

教材中解決這一問題時更建議根據題意假設把720毫升果汁全部倒入大杯或者全部倒入小杯，使原來含有兩個未知量的問題轉化為只含有一個未知量的問題，從而使較復雜的問題變得簡單。盡管教材也提出學生可以嘗試運用不同方法解決問題，但是方法之間的聯系常常被忽視。筆者在幾次學前調查中發現多數學生喜歡運用方程解決這類問題，所以學生常常有困惑：假設的優勢是什么？為什么老師沒有推薦用方程解題？筆者通過對比“小杯容量是大杯的[13]”和“小杯容量是大杯的[23]”兩個已知條件，引導學生感受到列方程解決問題適用范圍更廣，對數據沒有過多要求，而運用假設的策略解決問題過程簡單，但存在一定的局限性，對數據的要求較高，有時通過假設的策略轉化起來極具挑戰。這是我們站在學生的視角發現的學生的困惑。運用這種教學活動非常有意義，學生可以按照自己的想法去嘗試、去行動、去比較，所以他們在解決問題時會更加積極主動。

在自主探究過程中，我們發現：當一個未知量是另一個未知量的幾分之一時，數量關系直觀易于理解，學生會自覺想到一個未知量就是另一個未知量的幾倍，接著將兩個未知量假設成一個未知量。感受假設策略的簡潔、方便，經歷策略形成中“悟”的過程，而不是片面追求問題的解決。當一個未知量是另一個未知量的幾分之幾時，數量關系的理解極具挑戰，這時候列方程解答具有明顯的優勢，也是學生易于掌握的方法。教師根據學生的想法，引導學生按照他們自己的想法去探究，從而形成觀點與思想，這對于學生來說是最有價值的。

因為尊重學生的視角，才能讓學生體會到假設策略的優勢與局限性，因為站在學生的立場，才有可能看到學生思維的火花，因為把課堂還給學生，才使學生感受到方程的魅力。因此，教師應以學生為本，根據學生的想法推進教學，進而提升課堂教學效果。

作者簡介：高蘭（1990— ），女，江蘇淮安人，中小學二級教師，大學本科學歷，研究方向：小學教育。

（責編 劉小瑗）