力學課程一題多解對學生創(chuàng)新思維能力的培養(yǎng)探索

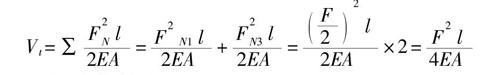
【摘 要】力學課程是工科院系的一門專業(yè)必修課程，它的理論體系、思維方法都很嚴密，系統(tǒng)性強，學生的用不同的定理、定律、方法，使學生學會不同角度的研究方法，得出不同層面的信息，以啟發(fā)、培養(yǎng)學生的創(chuàng)新意識。實踐證明，適時的運用這種方法，有效增強了學生思維的靈活性和開拓性。

【關鍵詞】力學課程;創(chuàng)新思維;能力培養(yǎng)

中圖分類號： G642;TB301-4 文獻標識碼： A 文章編號： 2095-2457（2019）35-0117-002

DOI：10.19694/j.cnki.issn2095-2457.2019.35.053

0 引言

力學課程作為大學工科院校的專業(yè)必修課程，旨在培養(yǎng)大學生的工程理念，解決工程中的實際問題和提高工程師的綜合素質(zhì)。當前教育界也在呼吁要培養(yǎng)學生的創(chuàng)新意識和實踐能力，面對越來越減少的課時和“卓越工程師培養(yǎng)計劃”的需求[1]，迫切需要教師快速適應教育形式的發(fā)展，從有傳授知識技能的培養(yǎng)轉(zhuǎn)向重視學生工程素質(zhì)創(chuàng)新能力的主動學習方式轉(zhuǎn)變。在實際教學的過程中，表現(xiàn)出的具體問題是，學生不主動思考，僅限于接受知識，看例題解答習題，知識應用很機械，稍改變邊界條件就出問題，不會綜合運用所學力學知識去分析問題、解決問題。如何提高學生的學習興趣和激情，引導和培養(yǎng)學生的創(chuàng)新意識和工程素質(zhì)等已引起了力學教育工作者的思考[2]。力學教學中的一題多解是指根據(jù)已知條件從不同的角度和知識系統(tǒng)去探求解題的不同思路[3]。一題多解能揭示基本概念所延伸的基本技巧，使知識形成完整的體系，不僅能幫助學生掌握從表面看似不相關的定理、核心知識點及解題步驟，加深對知識點的理解和掌握，而且能培養(yǎng)學生發(fā)散思維，有效提高學生思維的活躍性、靈敏性，激發(fā)學生的學習興趣和創(chuàng)新意識[5]。筆者以教材中的一道習題的求解問題為例，歸納總結(jié)不同求解方法的原理、核心知識點和解題步驟，深刻理解各種理論方法的內(nèi)容、應用條件、應用場合和特點，從而深化、活化各基本概念和基本規(guī)律的認識，提高學生分析問題和解決問題的能力。

1 問題和解法

1.1 問題示例

如圖1所示，梁BD為剛體，桿1、桿2與桿3的材料與橫截面面積相同，在梁BD的中心C，承受鉛垂載荷F作用，計算C點的水平與鉛垂位移。已知載荷F=20KN，各桿的橫截面面積A=100m2，彈性模量E=200GPa，梁長l=1000mm。

在授課過程中，學生的難點體現(xiàn)在對于這種桿系，不理解桿的伸長量與位移之間的關系，不會畫桿系的位移。

1.2 利用威利奧特圖解法

將圖1所示的結(jié)構(gòu)的三根桿截斷，軸力分別為FN1，F(xiàn)N2，F(xiàn)N3，如圖2。利用平衡條件

∑Fx=0，F(xiàn)N2cos45°=0

∑MB=0，F(xiàn)N3l-■F=0

∑Fy=0，F(xiàn)N1+F3+FN2sin45°-F=0

可得各桿的軸力

FN1=10KN;FN2=0;FN3=10KN

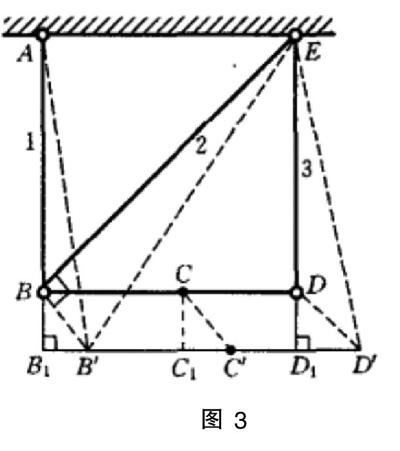
因桿2不受力，所以在外力F作用下，桿2不變形，只是隨桿1、3的變形而繞鉸接點E做剛體轉(zhuǎn)動，使點B移動到點B'，如圖3，桿1和桿3的軸力相等，所以它們的伸長也相同。由胡克定律有：

ΔL1=ΔL3=■=5×10-4m

變形后，剛性梁的新位置B'D'也就確定了，從而力F的作用點C的新位置C'也可確定，嚴格地說，點應該是以點E為圓心，以桿2即EB為半徑劃圓弧，與以點A為圓心，以桿1變形后的長度及AB1為半徑劃圓弧的交點，但由于是小變形，應用威利奧特圖解法，點可由過點B作EB的垂線，與過點B1作AB1的垂線，兩垂線的交點便確定了點B'，如圖3。由圖中的集合關系可知，點B的鉛垂位移BB1等于其水平位移B1B'，等于桿1的拉伸變形Δl1，由于剛性梁BD因桿1和桿3的變形只作剛體平移，所以力F的作用點C的鉛垂位移和水平位移與點B相同，即

ΔCx=Δl1=0.5mm（→）

ΔCy=Δl1=0.5mm（↓）

1.3 利用功能轉(zhuǎn)換原理

設在外力F作用下，力F的作用點的鉛垂位移為ΔCy，則外力作功為

W=■FΔCy

在求出三根桿的內(nèi)力后，如圖3所示結(jié)構(gòu)的應變能為

Vt=∑■=■+■=■×2=■

根據(jù)功能轉(zhuǎn)換原理，有

W=Vt，■FΔCy=■

所以力F的作用點C的鉛垂位移為

ΔCy=■=■=5×10-4m

力F的作用點C的水平位移與鉛垂位移相等，其分析與解法相同。

2 課堂效果評價

課堂教授兩種方法以后，提示大家這類題目還有更多的解題思路，例如卡式第二定理法，基于虛位移原理的能量法來計算桿系結(jié)構(gòu)位移計算;例如單位力法，作為能量法的另一種表達方式，單位力法主要用于求解線彈性位移;例如在能量法的教學過程中，利用單位力法推導出摩爾積分法，本題作為小變形的線彈性桿系結(jié)構(gòu)，能否應用等等。

學生的反饋很好，很多同學重新返回到知識點章節(jié)，主動學習，尋找解決辦法。問題解決了，知識點掌握了，知識點間的聯(lián)系也深刻理解了。更重要的是他們開始主動學習思考了。

3 結(jié)語

本文以工程力學教材習題中的一道習題為例，給大家講述了一題多解的教學方法，歸納總結(jié)了威力奧特圖解法，功能轉(zhuǎn)換原理，并引導學生嘗試了卡式定理、單位力法等多種求解方法的原理，涉及了力學課程中多個知識點，小變形放大圖、以切代弧、內(nèi)力計算、胡克定律、應變能和能量原理等。通過一題多解，學生能主動去學習，思考應用已學的力學知識解決同一個問題，把各章節(jié)學到的零散的、互不相關的知識點，通過思考、應用，把握各方面知識的聯(lián)系，形成一個完整的知識結(jié)構(gòu)。一題多解能夠打破學生平時解題形成的一種先入為主的思維定式，培養(yǎng)學生的創(chuàng)新思維能力。

【參考文獻】

[1]林健.卓越工程師創(chuàng)新能力的培養(yǎng)[J].高等工程教育研究，2012（5）：1-17.

[2]余志紅.教學與科研結(jié)合的力學課程的設計探索[J].科技視界，2019（6）：32-34.

[3]張淑芬，梁斌，楊民獻.力學課程教學應突出學生素質(zhì)培養(yǎng)[J].洛陽理工學院學報（自然科學版），2008（1）：91-93.

[4]蔡傳國.本科力學實驗中的創(chuàng)新思維培養(yǎng)方法探索[J].力學與實踐，2013（6）：95-96.

[5]孫訓芳，方孝淑，關來泰.材料力學（I）[M].第5版.北京：高等教育出版社，2009.10.

[6]曲艷東，賈艷東，孔祥清，等.材料力學一題多解談創(chuàng)新[J].遼寧工業(yè)大學學報（社會科學版）.

[7]單輝祖，謝傳峰.工程力學（靜力學與材料力學）[M].北京：高等教育出版社，2004.1.