淺談初中數學教學中如何滲透化歸思想
摘?要:在新課程改革的影響下,傳統教學模式和教學方法的改革和創(chuàng)新也在逐漸深化,以培養(yǎng)學生核心素養(yǎng)為中心的基本教學原則逐漸被廣大教師所認可并實施,強化課堂教學效果是提升學生綜合素質和能力的關鍵途徑。初中數學是國民教育體系中的重要基礎學科,不僅能夠有效激發(fā)學生的創(chuàng)新思維,還可以為后續(xù)的學習和成長奠定堅實的基礎。為了提升初中數學教學的效果,可以從化歸思想的角度對課堂教學進行滲透,充分利用化歸思想的內涵培養(yǎng)學生的數學核心素養(yǎng),以此提升學生的綜合素質。
關鍵詞:化歸思想;初中數學;滲透;策略
從初中教育教學體系設置的角度來看,數學無疑是所有學科中的最為重要的構成部分之一,通過數學知識和能力的學習和訓練,有助于培養(yǎng)學生的邏輯思維能力和創(chuàng)新能力,因此,初中教育應該強化數學教學的效果。由于初中數學的知識和理論比較多,融匯數學思想的教學內容也比較豐富。加強數學課堂教學,實際上不僅可以培養(yǎng)學生有效運用數學知識和能力解決實際問題,還可以促進學生的個人成長和發(fā)展,不論從學校教育成效的角度考慮,還是學生個體成長成才的角度考慮,都應該強化初中數學課堂教學。化歸思想是所有數學思想中比較特殊的內容,同時也是引領學生掌握數學邏輯思維的重要內容,教師通過將化歸思想融入課堂教學內容,引導學生利用化歸思想解決學習和生活中的實際問題。因此,初中數學教師應該認識到化歸思想對數學課堂教學的積極作用,強化教學設計和教學研究,將化歸思想有效應用和滲透到課堂教學環(huán)節(jié),以此提升初中數學課堂教學的效果。
一、 化歸思想概述
初中數學思想本身內涵豐富,常見的包括方程思想、數形結合思想、化歸思想等。數學思想是數學學科的精髓部分,掌握數學思想實際上是從方法論的角度把握數學學習的本質,因此,從初中階段開始向學生傳遞數學思想是有必要的。通過數學思想的講授,可以大力提升學生的數學方面的綜合素質和核心素養(yǎng)。在上述常見的數學思想中,化歸思想可能是實際教學中應用最為廣泛的一種。初中數學教師如果能夠科學、合理地將化歸思想滲透到課堂教學環(huán)節(jié),那么勢必會大幅度提升課堂學習效率,起到事半功倍的效果。
所謂化歸思想,實際上是指將復雜的數學問題轉化為簡易的數學問題的過程,這種化難為易的思維本身就是一種思想和方法上的雙重效應的體現。將化歸思想融入初中數學課堂教學環(huán)節(jié),可以將很多本身較為復雜的數學問題進行簡化。一方面可以訓練學生的邏輯思維能力,培養(yǎng)良好的思維習慣,另一方面還可以引導學生探究數學真理,激發(fā)其創(chuàng)新意識。因此,將化歸思想滲透到初中數學課堂教學是應該大力提倡的。
二、 初中數學課堂教學中滲透化歸思想的策略
(一) 化歸思想在代數教學和學習中的應用策略
在初中數學課堂教學中滲透化歸思想,最為典型的應用便是在代數教學和學習過程中。應用化歸思想,可以讓學生將代數問題的內涵進行簡化,進而提升解題的效率,經過長期的訓練和灌輸,學生的學習效率和質量都會得到大幅度提升,最終促進其數學核心素養(yǎng)和綜合能力的提升。初中數學代數部分的教學內容與小學數學的基本運算內容關聯度較大,對代數的教學實際上就是建立在小學數學知識的基礎之上,經過一定的延伸和演化成為代數知識和內容。
在教學中,教師可以借助化歸思想將初中代數教學內容轉化為小學數學的基本運算形式。這樣的處理,一方面可以讓學生將不熟悉的代數學習內容轉化為熟悉的小學數學知識,另一方面還可以讓學生在參與數學學習的過程中不斷豐富自己的學習方法,提升學習效率。將復雜的代數內容以化歸思想的模式進行簡化,能夠更好地調動學生的學習積極性和主動性。
例如:學生在學習分式方程的時候,教師可以對學生的學習過程進行引導,將化歸思想的內涵融入分式方程學習過程中,通過轉化,能夠將分式方程轉化為整式方程式,而整式方程式的解題方法則相對較為簡便,可以快速被學生所理解和掌握。經過這樣的處理,學生在學習相關代數知識的時候就能夠更加得心應手,不僅鞏固了數學學習內容,同時也鍛煉了邏輯思維能力。
(二) 化歸思想在平面幾何教學和學習中的應用策略
初中數學的教學內容中,平面幾何的內容也是其中的重要組成部分,化歸思想在平面幾何教學上的應用同樣效果顯著。從平面幾何的內涵角度來看,其內在的邏輯思維結構的形成對于提升學習效果至關重要,而化歸思想能夠幫助學生從根本上提升自身的理解能力,從而抓住平面幾何解題技巧和方法,最終達到高效完成學習任務的目的。
例如:學生在接觸多邊形的圖形知識時,教師可以將多邊形經過變換轉化為學生所熟悉的三角形的圖形進行解題(如下面的中考題型)。
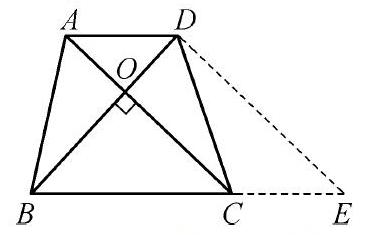
如圖在梯形ABCD中,AD∥BC,AB=CD,對角線AC、BD相交于O點,且AC和BD相互垂直,AD=3,BC=5,求AC的長。
在該題型中,便可采用化歸思想來進行轉化,經D點作DE∥AC的輔助線,交BC延長線于E點,在此過程中利用該梯形對角線相互垂直的特點,可知DE⊥BD,且DE=BD,順利將梯形轉化為等腰直角三角形和平行四邊形,從而使問題得到解決。
又比如立體圖形的側面積的計算時,往往我們用展開法進行轉化。其實這種展開法就是化歸思想的實際應用,化立體為平面,化陌生為熟悉,轉化為平面圖形解決問題,學生很容易理解,從而降低了學習難度。在上述的轉化過程中,化歸思想的應用能夠起到化繁為簡、化難為易的作用,學生也能夠逐漸在教師的引導下學會運用相應的技巧和方法,進而提升解題效率和質量。一旦學生掌握了化歸思想的精髓,他們就能夠在平時遇到其他數學問題時,應用化歸思想解決一些未知的問題,達到自主學習的目的。
(三) 化歸思想在解析幾何教學和學習中的應用策略
解析幾何也是初中數學教學內容中的疑難內容,初中數學教師也可以應用化歸思想將看似繁復的問題進行處理,通過一定的技巧和方法對相關內容進行簡化,進而降低相應問題的解答難度,激發(fā)學生的學習興趣和熱情。
以“函數及圖像”中的直線交點問題為例,化歸思想的應用可以達到化腐朽為神奇的效果。例如以平面直角坐標系為基礎,求坐標系中的不平行的兩條直線的交點,如果利用圖像法求交點將會非常煩瑣,若利用化歸思想進行處理,也就是數學問題中常見的解方程組內容。假設兩條直線為L1和L2,對應的方程分別為:A1x+B1y=C1?①,A2x+B2y=C2?②。由①和②就可以組成一個方程組,通過解方程組得出x和y的具體值,通過坐標系中交點的表述,可以確定兩條直線對應的交點坐標為A(x,y),顯而易見A點同時在兩條直線上。最終得出結論:A(x,y)既在直線L1上又在直線L2上,同時A(x,y)也滿足兩條直線交點的條件。以這樣的方式可以將解析幾何中的相關問題進行簡化,進而提升學生的解題效率。
三、 注重日常教學,滲透和落實化歸思想
化歸思想對于學生解決較為復雜的數學問題有著舉足輕重的作用,但是每一種思想的形成絕非一朝一夕的事情。這就要求教師在日常教學中重視和落實化歸思想的滲透。
(一) 培養(yǎng)化歸意識,享受由化歸思想解題帶來的歡樂
作為一個有機的整體,數學各個組成部分互相聯系,相互滲透,相互融合,形成了一張縱橫交錯的知識網絡。所以,我們在解決數學問題時,必須引導學生找準知識之間的聯系,嘗試能否用化歸思想來解決問題。在解題的過程中有目的、有計劃的培養(yǎng)學生的轉化思想。在實踐中,一是引導學生分析題目告知的已知條件,明白求解的目的;二是要幫助學生學會根據已知條件和解題目標,聯系學過的有關數學知識,例如涉及的定義、公式、定理、推論等,建立已知問題和未知問題的橋梁,做到化陌生為熟悉,找到解題的思路和方法,享受由化歸思想解題帶來的歡樂。
(二) 注重基礎知識,是落實化歸思想教學的先決條件
扎實的數學基礎知識,完備的數學知識結構,是落實化歸思想教學的關鍵。因此,在教學中我們要想方設法夯實學生的數學基礎知識,完善學生的知識結構,只有這樣才可能真正落實化歸思想教學。首先,要重視數學基本模型的教學。從某種意義上來說,數學教學就是數學模型的教學。而教材涉及的定義、公式、定理、推論等是基礎的數學模型,離開這些基礎知識談化歸思想教學無異于緣木求魚。所以說,定義、公式、定理、推論等的教學尤為重要,教學時要深挖基本概念的內涵和外延,注意公式、定理、推論等適用范圍。其次,注意引導學生構建知識網絡,完善知識結構。知識結構的缺失,是學生解題時的最大障礙。要建立完善的知識結構網絡,在平時的教學中要幫助學生搞好單元總結,比如,利用思維導圖使已學過的知識系統化、板塊化。這樣一來,知識之間的聯系一目了然,有利于學生在此基礎上將各部分內容融會貫通。再次,注意總結解題思路和方法。優(yōu)秀的學生其實是多掌握了解題思路和方法的人。培養(yǎng)學生形成良好的總結思路和方法的有效途徑就是反復揣摩經典習題,對思路和方法深入領會,為以后解決其他問題提供一些方向性的指導。
(三) 依托教材,掌握化歸的一般方法
教材中蘊含著很多的化歸思想方法,在教學中要注意提煉和總結這類方法,讓學生切實感受到這類方法的存在及優(yōu)點。在定義概念的形成過程中,在定理、公式的應用過程中滲透深化化歸思想,在解決問題的過程中領悟化歸思想的精髓,做到新舊知識之間的轉化,一般和特殊之間的轉換。熟練掌握分解法、配方法、待定系數法、換元法、坐標法等常見的化歸方法。
綜上所述,化歸思想的應用對于初中數學課堂教學的作用非常顯著,廣大教師應該將化歸思想的內涵滲透到課堂教學過程,鼓勵和引導學生以化歸思想為導向,將復雜的數學難題進行簡化,一方面可以鍛煉學生的邏輯思維能力,提升數學核心素養(yǎng),另一方面也可以從化歸思想的應用中得到啟發(fā),促進其創(chuàng)新能力的培養(yǎng),進而提升其綜合素質和能力。
作者簡介:
周厚芳,甘肅省蘭州市,甘肅省永登縣第七中學。

