試論小學數學教學中數形結合思想的滲透

曾和平

【摘要】數學是表示空間形式和數量關系的學科。它的研究對象就是數與形。而數是形的抽象概括，形是數的直觀展現。因而我們小學數學教師應靈活地運用數形結合的思想解題，提升小學學生的教學水平。

【關鍵詞】小學數學;數形結合;教學策略

抽象性是小學數學的學科特點。我們小學數學教師可以運用數形結合的思想講授教學知識，從而讓學生非常直觀地掌握教學內容的同時，感受數學教學的趣味性，增強學生學習數學的信心。此外，我們也要讓學生認識到數形結合的局限性，使其能夠靈活運用數學結合的思想，提升學生的解題質量。

一、以數解形——復雜問題簡單化

小學數學教師在教學的過程中可以運用以數解形的思路解決數學問題，引導學生思考圖像性質與數字之間的關系，并列出相應的等式，從而將復雜問題簡單化，促進學生思維的完善。與此同時，教師要鼓勵學生積極地發言，并對學生的思路予以贊揚，激發更多的學生參與到教學活動中來，提升整體的小學數學教學水平。

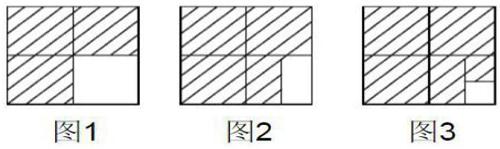
比如，在講授《異分母分加減法》這節內容時，我鼓勵學生積極地發言，闡述其思路，最后，為學生講述以數解形的教學方法，從而既拓展了學生解決問題的思路，也讓數形結合的思想融入教學中，提升數形結合的教學質量。具體操作如下：首先創設問題。我板書了如下三個計算題。（1）1/2+1/4=？（2）1/2+1/4+1/8=？（3）1/2+1/4+1/8+1/16=？其次，我詢問學生：“你們可以計算出這三個問題的答案嗎？我給你們10分鐘時間！”學生迅速投入到計算中。再次，詢問做題結果。在學生做題結未后，我詢問學生：“誰可以分享自己的計算的結果？并說出自己發現了那些規律！”小陳說：“后一個計算題比前一個依次多1/8和1/16，我運用通分的方式進行計算的，它的答案為3/4、7/8和15/16！”我微笑說：“你的答案非常正確！”從此，出示圖形，引導學生運用數形思想解決問題。我運用多媒體出示了如下的三個圖形，對學生說：“你們能在下面的圖形中找到和上面三個式子的關系嗎？我給你們三分鐘的時間回答！”

小寓積極地舉手回答：“圖1就是第一個算式，而圖2就是第二個計算題，圖3則為第三個算式！”我微笑說：“很好！你們可以運用圖表計算陰影部分的面積么？可以充分觀察，并發揮自己的想象力！”小洛說：“我可以算出來，比如第一個圖1一共有3個1/4;圖2有7個1/8;圖3有15個1/16”我微笑說：“你很好地應用了圖形，你們可以去掉空白處的面積，就可以得到整個圖形的陰影面積，你們想一想有沒有新的思路？”小艷興奮地站起身說：“圖1的面積為1-1/4;圖2的面積為1-1/8;圖3的面積為1-1/16，而這三個答案和我們計算的答案相同！”我點點頭說：“你的回答非常正確！”我尊重學生的想法，鼓勵其積極發言，既鍛煉了他們的數學計算能力，又適時地插入數形結合思想，使學生可以前后對比加深對于數形結合的理解，從而增強了數形結合的教學效果。

二、以形助數——考由象問題形象化

以形助數是借助形的直觀性展示其與數之間的關系。教師可以根據數量的結構特征，將其轉化為幾何問題，從而建立幾何與數之間的對應關系，讓學生充分地運用題目中給出的條件，激發學生解題靈感。在小學數學中分數應用是教學中的難點和重點，因而學生的學習比較困難，我們可以借助數形結合的思想開展教學，從而幫助學生培養數學結合的思維，激發其學習數學的興趣，提升整體的小學數學教學質量。此外，我們應尊重學生特有的思維，鼓勵其勇于創新，培養學生學習數學的信心。

比如，在講授“分數應用題”這節內容時，我運用以形助數的思維開展教學，并鼓勵學生進行大膽發言，激發學生的學生學習數學的積極性。具體操作如下：首先，創設問題。我板書了如下的問題：一箱蘋果，第一次拿走1/2，第二次拿走剩下的1/2，還剩下4個，問題為這箱蘋果一共多少個？其次，適時引導。我對學生說：“你們可以運用自己學過的知識解決這個問題！”再次，詢問結果。在學生討論結束后，我詢問學生：“誰可以分享自己討論的結果？”小碧主動舉起手說：“我用設未知數的方法進行計算的，即將一箱蘋果的數量設為X，第一次拿走的是（1/2）X，第二次拿走的為（1/4）X，則剩余的為（1/4）X，則最后答案為16個蘋果！”我微笑說：“你的答案很好！”從次，教授以形助數的解題方法。我對學生說：“我們可以運用數形結合的方式，充分將題目給出的條件，轉化到圖形上，激發我們的思路！我們可以將雞蛋的數量設為單位‘1！”我展示了如下的圖片：

我對學生說：“你們通過看圖能得出什么結論？”小悅說：“圖中將題中給出的條件充分運用到了圖形中，非常直觀地看出剩余雞蛋的數量為16個！”我點點頭說：“我們可以將數學題中給出的條件以畫圖的形式展現出來，從而理清自己的思路，激發自己解題的靈感，數形結合思想是我們最常用的解題思路！”我運用數形結合的思路，使學生可以和原有的解題思路進行對比，幫助學生樹立數形結合的思想。

三、結合實際教學——認識數形思想的局限性

小學數學教師可以引導學生將問題中的數量關系轉化為對應的圖形關系，從而使得抽象的問題，直觀化地展現出來，并分析所給條件在圖形中的相互關系，從而得出正確的解題思路。值得注意的是小學數學教師要靈活地運用數形結合思想進行教學，既要看到這種教學思想的優越性，又要能夠了解它的局限性，從而幫助學生熟練掌握各個解題思想的應用條件，提升學生的解題速度和質量。

比如，在講授應用題時，我會根據具體情況引導學生運用數形結合的思想解題，從而讓給學生認識到數形思想解題的局限性，對這種數學解題思路有了更加全面的認知。具體操作如下：首先，創設問題。我運用多媒體展示了如下的問題：小鴨和小狗同在一個籠子里，一共有20個頭，54條腿，問題為小鴨和小狗各有多少只？其次，鼓勵學生思考。我對學生說：“你們可以運用自己的思維思考，能否得出正確答案！”再次，詢問學生的解題答案。我看到大部分的學生解題結束后，便詢問學生：“誰可以分享自己的探究結果？”小秀說：“我設小鴨的數量為X，則小狗的數量為（20-X），得出等量關系式為2X+（20-X）X4=54，得出有小狗7只，小鴨13只！”我點點頭說道：“你的方法很好！我們可以運用畫圖的方式進行分析，你們可以運用畫圖的方式將題中的條件充分運用！你們要仔細分析小鴨和小狗的腳的數量的不同！”最后，詢問結果。在學生探究完畢后，我適時地詢問學生：“誰可以分享自己的探究成果？”小華舉手說：“因為小狗比小鴨腿的數量多，因而多出去的腿的數量為小狗的2倍，即多出去的腿的數量是14，則小狗的數量為7，小鴨的數量為13！”我拍拍他的肩膀說：“很好，我們可以對比前后兩種方法，我們可以很直觀地看到，數形結合有其一定的優勢，也能夠非常清晰地展現教學內容，但是如果題目中的數量增大，而數形結合的思想就存在一定的局限性，而列方程進行解題的方式會更加適用！因而我們要注意使用數形結合的具體條件，具體分析各個解題方法的應用條件，從而最佳的解題方案，提升解題速度和正確率！”我運用數形結合的思路，并鼓勵學生進行發言，使學生認識到數形結合解題思路的局限性，從而使其對于數形結合思想有了更加深刻地認識，提升整體數學教學的質量。

總結

數形結合思想在解答和講授教學內容方面有很大的優勢，但是我們小學數學教師也應看到其解題中的局限性，并教授學生正確掌握數學結合思想應用的條件，提高小學數學的教學質量。

【參考文獻】

[1]畢娉婷.數學教學中數形結合思想的應用分析[J].教育現代化，2017（15）

[2]孫玉橋.小學數學教學中數形結合思想的滲透研究[J].中國校外教育，2017（20）

[3]連作鵬.小學數學教學中數形結合思想教學模式初探[J].中學課程輔導（教師教育），2016（06）