因“生”制“練”用“活”教材

范琰

摘 ?要：新教材關注學生獲得知識的過程，注重探究能力和學習習慣的培養。筆者從教學實踐中學生練習的難度來反觀新教材，發現有些例題、習題的配置欠合理。教師在利用教材時，要有科學的教材解讀觀。深入研究編者意圖的同時也要根據學情，因“生”制“練”，對例題與習題進行合理的布局、刪減、增加、轉換。使知識點的落實更富有張力，使之適合學生知識的掌握、框架的建構和能力的提升。

關鍵詞：小學數學;例題;整體把握

教材是編者設置承載知識的一個載體。教師在運用教材時，要有科學的教材解讀觀。深入研究編者的意圖同時也要根據學情，以生為本，因“生”制“練”。利用好例題與習題進行合理的刪減、轉換、增加。使知識點的落實富有張力，使之適合學生知識的掌握、綜合解題能力的提升，從而提高教學質量。本文以五年級《植樹問題》單元為例，談談在課堂教學中，例題與習題配置層次性、互逆性、溝通性、開放性等方面的適度把握。

一、由此及彼，拓寬思維，學法遷移由單一走向多元

課本例題所承載的是單一的知識點，有效的習題設計能讓這個知識點向著各個方向輻射。很多學生由于思路閉塞無法真正拓寬思路，這正是因為他們聯想的羽翼不夠豐滿。他們總是孤立地看待問題，而沒有由此及彼地尋找問題間的本質聯系。這種“思接千載”“視通萬里”的聯想能力也需要在課堂上加以鍛煉。從而使我們的學法遷移由單一走向多元。例如：

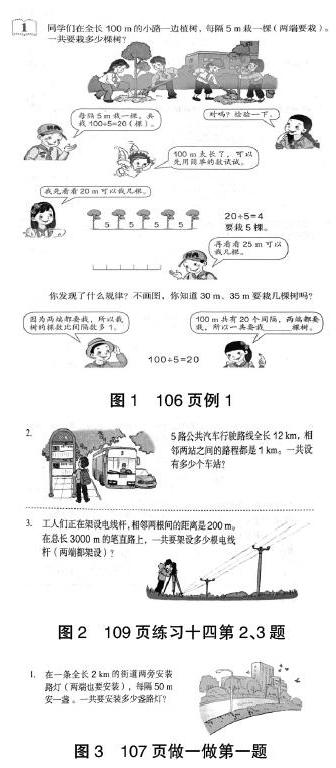
在講解完例題1后，整合了圖2練習十四第2、3題和圖3做一做的第一題。教師把三個題組一起，讓學生先讀題，留足時間讓他們思考。

師：這三道題有什么共同之處嗎？它們和例題有什么聯系嗎？

在讀完題停留30秒后，留給孩子思考的空間。有孩子舉手說：“我覺得這三道題屬于植樹問題兩端都栽的情況。”

師：“你能說說想法嗎？那相當于求什么呢？”

生：“相當于植樹問題里的樹。如第2題中，可以把12千米看作植樹的總長，相鄰路程1千米看作植樹的間隔距離，求多少個車站就看作求植樹的棵數。”

當學生如此清晰地表達習題與例題的相似點時，題組的練習目的也就達到了。學生能由此及彼，由例題的學習想到習題的拓展，清晰地建立起關系，做到真正的溝通聯系、舉一反三。

二、化靜為動，拾級而上，解題能力由模仿走向創造

教材中的例題與習題是靜態呈現的。它只是為知識的傳遞提供了可能。但是我們的課堂教學是活的，是富有生命力的。如何運用化靜為動，為我們的教學提供更多靈動的素材，這就需要我們的教師有一顆深究的心和科學的教材觀。教材的呈現方式是靜態的，有些看似簡單的教學內容，往往蘊藏著豐富的數學內涵，這時就需要教師針對內容的特點和學生的實際情況去深挖和拓展。例如：

2. 小紅要給一塊長48厘米、寬36米的長方形的四周繡花。她每隔6厘米繡一朵花，四個角上個繡上一朵花，那么她一共要繡多少朵花？

3. 圓形的跑道插著100面小旗，兩面小旗的間隔是4米，如果現在想插80面，間隔應為多少米？

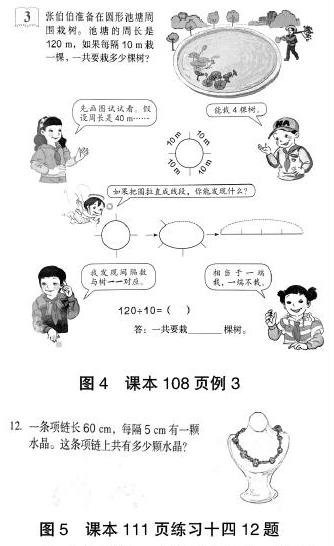
在例題3的學習之后，筆者安排了3道層次豐富的習題。第一題是課本111頁12題，這題只是知識的遷移，由種樹問題演變成求項鏈上的水晶，同類型便于學生溝通。對學生來說是例題的變式，難度不大。第二題讓學生獨立完成，對于中下以上的學生，感覺有點困難，而好的學生的適時點撥，就能讓他們恍然大悟。重在溝通長方形、正方形等也是屬于封閉圖形，和圓形異形卻同理。第三道練習突破求植樹問題中的棵樹模型，是對這種數學模型的綜合運用，已知小旗的面數和間隔距離，根據面數與間隔數相同，可以求出跑道的總長，再根據改后只插80面，可以求出改后的間隔長度。

學生接觸新知識，對知識的掌握是一個循序漸進、螺旋上升的過程。它靠慢慢地累積、不斷地對比、仔細地甄別來完成對新知識的建構。有層次的練習題正是學生完成這種構建的載體，它能不斷在學生的“最近發展區”的基礎上對知識進行逐步的提煉、建模、深化。

三、由順而逆，適時轉換，思維能力由機械走向靈活

傳統教育以正向思維為主，導致學生解題中思路僵化，模式化明顯，不能靈活地應用知識。在實際教學中，通過對學生進行邏輯性較強的逆向思維的引導，讓學生從不同的角度思考問題，擺脫思維定式，加深對知識的理解。所以適時將練習進行逆向轉換，由正及反，正反并舉，引導學生思維的逆向思考，使學生的思路更加靈活、深刻。例如：

2. 從教學樓到食堂有一條筆直的通道，通道的一邊種了44顆樟樹，相鄰兩顆樟樹的距離是5米，從教學樓到食堂有多遠？

在教學了例題2后，筆者安排了2道練習題。第一題來自109頁練習十四第6題，第二題來自課堂作業77頁第5題，整合了兩道互逆的練習題。

在第一題的安排上，抓住知識的連接點，利用例題與習題的關系，順勢而導。學生根據經驗自主加工構建。而第二道練習，抓住知識的生長點，通過已經種了的44棵樟樹，可以求什么？又根據教學樓和食堂相當于植樹問題中的兩端都不種，可以反過來求出間隔數就是55個。這樣把學生思維由正面帶向反面，理清學生的思路，理順對關系的思考與理解。教師應充分培養學生的雙向思維能力，學會從不同角度看問題，提高學生思維的品質。

四、由點到面，補齊知識，認知結構由平面走向立體

數學教材是數學知識體系的階段反映。各例題之間的相互融合成就了一種數學思想。課本的例題往往只是一個知識點呈現，而習題的安排有可能就是知識點的補充或是對應的知識點。那么零散的知識點如何成為一條條知識鏈，一條條知識鏈又如何形成一個個知識面呢？這就需要我們教師站在一個制高點上去審視和把握教材，學會正確處理習題的關系，必要時對有些習題進行顛三倒四，適時整合;把典型習題處理得厚重一些，厚此薄彼;甚至可以像教學例題那樣詳盡，以此來補齊學生的知識斷面。例如：

1. 同學們軍訓，站成方隊的最外層每邊站了16個，最外層一共有多少名學生？

2. 同學們站成方隊進行軍訓，知道最外層一共站了68人，那么最外層每邊站了多少人？

課本111頁練習二十四第14題并不是一道例題，而是一道普通的習題。但它是一個重要的知識點，是一種典型問題。我們教師在處理它時不能一筆帶過，而是濃墨重彩。我們不僅要花足夠多的時間幫助學生理清數量關系，還要融會貫通它的變式題，把一個個潛在的知識激發出來，以此補齊知識斷面，向學生傳遞一個完整的數學模型，幫學生建立一個融會貫通的網狀知識結構。

五、由表及里，溝通聯系，知識結構由孤立走向系統

在點狀的例題知識學習之后，教師可以把每個知識點進行巧妙融合，放置到更廣闊的背景下“聯結”。這不僅能有效盤活知識間的聯系，而且有助于學生多角度地理解知識，綜合地分析和應用知識，悟到數學知識內部間的融合關系，使知識結構由孤立、無序走向系統、完整。例如：

A、為迎接“六一”兒童節，學校準備在8米長的主席臺上放盆花（兩頭都不放），每相鄰的兩盆盆花之間的距離是50厘米，那么學校需要準備多少盆盆花？

B、丁丁在練習滑輪繞樁時，一共放了20個樁，每兩個樁之間的距離是80厘米，那么首尾兩個樁之間的距離是多少米？

C、公園正門正對的一條筆直的公路長120米，現要在公路兩邊種梧桐樹，每兩棵樹相距6米。園林工人共需要準備多少棵樹？

在教學完三個例題的練習課中，筆者安排了讓學生解答ABC三道練習題。先讓學生進行獨立解答，再同桌進行交流，在反饋完3道題目之后，課件顯示出植樹問題的三個例題。讓他們找找看三道題目與三個例題的聯系。給他們足夠多的時間思考。

生：我覺得A和例題2可以歸為一類，B和例題1是一類，而C又和例題3歸為一類。

師：說說你的看法，為什么屬于一類？

生：A題和例題2都是屬于兩端都不種的植樹問題，B題和例題1是屬于兩端都種的植樹問題，而C題和例題3屬于只種一端的植樹問題。

師：這兩組題目有什么區別嗎？

生：有區別的，例如B題和例題1雖然都屬于兩端都種的植樹問題，但是例題1是已知總距離和間隔距離求棵樹，而B題就相當于植樹問題里的已知棵數和間隔距離求總距離。

整節練習課目標的制定與教學過程的展開緊密相連，環環相扣。教學過程的展開就為目標的達成服務，圍繞著學生對知識的整理和構建模型的完成。由習題引回例題，比較題組與3個例題的聯系和區別。以學生的觀察能力、探究能力和學生的合作能力為主要目標，為學生對單元知識點的建構搭建了一個合理的支架;溝通知識之間的本質聯系，使學生構建起完整的單元知識的立體框架。

教材是學生學習數學的第一手資料，是傳遞知識點的載體。正確的教材觀絕不僅僅止于如何“用教材教”，同時應該倡導動態、立體、豐滿、靈動充滿文化張力的科學的教材解讀觀。我們一直相信，教材是靜態的，但是編者、教師、學生是有著火熱生命的。每一張靜默的圖片背后可能蘊含著豐富的數學思想，每一個簡單的算式深處可能飽含著火熱的數學思考。教材并不是枯燥乏味的，而是生動活潑的;不是“線性靜止”的，而是“立體靈動”的。