初中數學一次函數教學策略探微
饒德志

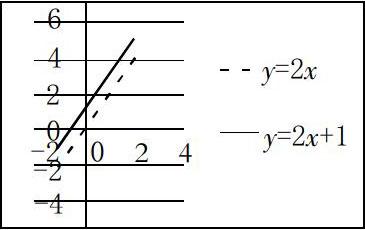
摘 要:一次函數教學是初中數學教學的重點內容之一。從學生認識函數概念,積累基礎知識,理解把握函數思想,到解決具體問題,需要一個系統性、高效性的教學方案和教學過程。文章通過解析課堂導入、教學重點、本質思想,具體闡述初中數學一次函數教學的教學策略。
關鍵詞:初中數學;一次函數;教學策略;課堂導入;教學重點;本質思想
中圖分類號:G633.6文獻標志碼:A文章編號:1008-3561(2019)30-0058-02
一次函數是初中二年級數學教學的重點知識內容,它在一元一次方程(初中一年級上)、一元一次不等式(初中一年級下)、平面直角坐標系(初中二年級上)的基礎之上,第一次向學生提出了函數的概念,并且第一次向學生展示了函數與圖形、函數與方程、函數與不等式之間的關系。這是學生函數概念的入門,也是數形結合思想、劃歸思想的重難點。如何有效開展一次函數教學,也是整個初中數學教學的重點和難點。初中一次函數教學實際上是致力于幫助學生形成函數概念、樹立建模意識、體味數學思想的過程。想要做好一次函數的教學工作,教師可以從以下幾個方面著手嘗試。
一、課堂導入:函數概念與建模意識
在一次函數之前,學生已經分別學習了一元一次方程、一元一次不等式、平面直角坐標系,對變量之間的關系和坐標系都有了一定的了解。而函數實際上就是通過解析式、圖像、表格等方式表示變量之間的關系的數學工具。從這個角度來看,引入實際問題來幫助學生了解函數概念是可行的。
對于上表,教師可以通過“給定兩分鐘時間,小明用不同的速度走了不同的距離,這兩者之間有什么關系”這類問題引發學生思考。在學生的常識里,同樣的時間內,速度越快,行進的距離越遠。學生意識到這一點后,很容易就能理解速度與距離之間有一定的關系。這時,教師可以不用著急給出“y=2x”的表達式,而只是引導學生發現速度與距離成兩倍關系,再通過下面的例子幫助學生樹立函數概念與建模意識。例題:班長去采購筆記本,每本3元錢,班級共50人,采購完成后還需付給商店15元的搬運費。每人的筆記本數和最終需要付的費用之間有什么關系?教師可通過這個問題,引導學生列出下表。
最終請學生回答“總費用和每人筆記本數之間的關系能否用一個表達式表達出來”,再引導學生寫出表達式“y=150x+15”。這樣,學生可以身臨其境地感知和理解變量之間的相互關系,并用表達式或表格的形式表達出來,對函數的理解也就自然而然地完成了。
二、教學重點:基礎知識與基本技能
一次函數的基礎知識主要包括:①函數的概念(變量與常量;函數定義;定義域及其確定方法)。②函數的性質(y與x成正比例,比值為k;b為截距;正比例函數;兩個函數在坐標系中的位置關系)。③圖像性質(作法;圖像特征)等。學生應掌握的基本技能包括:能夠找出常量和變量,建立、表示并討論函數模型,解決實際問題;數形結合分析函數關系;運用劃歸思想分析一次函數、一元一次方程及一元一次不等式之間的關系。本章的教學重點就在于幫助學生在建立函數概念與建模意識的前提下,準確掌握上述知識,并學以致用,解決實際問題。
教師應先引導學生熟悉并熟記一元一次方程的基礎知識。尤其需要注意的是,不能采用填鴨式教學方法,生硬地把知識灌輸給學生。教師可利用下表表示“兩個函數之間的位置關系”這個知識點。
然后,教師可引導學生結合具體圖像去探求兩個函數之間的關系。以k、b均相同,兩函數圖像平行為例,可以給出y=2x、y=2x+1的函數圖像,通過圖像上的直觀表現來加深學生對知識點的理解。
對于學生基本技能的養成,則需要通過列舉典型例題,幫助其形成一般解題思路和解題方法,并嘗試舉一反三。例題:函數上兩點與函數表達式的互相求解問題。一般的題型如下:已知一次函數y=kx+b的圖像經過(1,3),(-1,-1)點,則函數表達式為____。這類題目只需將點坐標代入y=kx+b,然后求解一個二元一次方程組即可。
幫助學生理解上述題目的解題思路后,教師可以列舉這類題目的變形,如:“已知函數y=x-3與y=2x+2的交點為(-5,-8),則方程組x-y-3=02x-y+2=0的解是____”,引導學生加深對這類題目的認識。
三、本質思想:數形結合與轉化劃歸
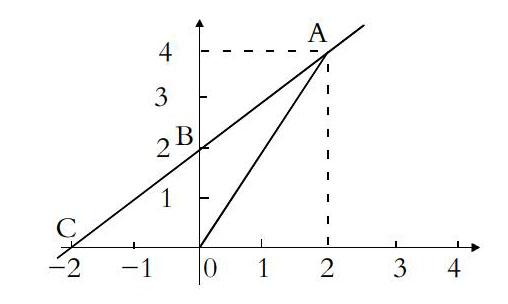
下面以一個例題來說明一次函數問題中包含的數形結合與轉化劃歸思想。如圖,一次函數y=kx+b的圖像經過A、B兩點,與x軸交于點C,求:(1)該一次函數的解析式。(2)△AOC的面積。
第一問本質依然是給定兩點求函數解析式,需要將其轉化劃歸為二元一次方程組,將k、b作為未知數進行求解。只需將A(2,4),B(0,2),C(-2,0)中任兩點坐標代入y=kx+b,即可求出k、b的值。第二問通過數形結合思想解答,則更加簡單:△AOC的一邊為OC,其長為點C橫坐標的絕對值,OC上的高則為點A的縱坐標值,則可求得其面積。
從中可以看出,一次函數問題,幾乎充滿了數形結合思想與轉化與化歸思想。實際上,對于函數本身的研究,以及對于函數相關問題的研究,其主要思想工具便是數形結合思想和轉化劃歸思想。在教授一次函數這一章時,教師應當時常向學生強調這一本質思想,引導其抓住問題的本質與關鍵,再進行思考與解題,這對學生的解題能力和思考習慣的培養,都是大有裨益的。
總之,一次函數是初中數學中最為重要的章節,作為學生面向函數知識與函數思想的敲門磚,其意義重大。在一次函數教學中,教師要做到的,是幫助學生樹立建模意識,打牢基礎知識,并在此基礎上熟練掌握數形結合與轉化劃歸思想。學生只有掌握了上述內容,才能真正做到對一次函數心中有數,筆下有靈,真正掌握函數的精要與關鍵。
參考文獻:
[1]甘宗全.如何教好初中數學一次函數[J].中學教學參考,2018(02).
[2]孫凱.基于深度學習的數學探究——以“一次函數的圖象(2)”教學為例[J].中學數學月刊,2018(10).
[3]孫凱,劉德水.初中數學小專題課的教學策略分析——以“一次函數圖像下的三角形面積問題”教學為例[J].數學教學,2018(10).
[4]鄧子薇.初中數學教學中“教思考”的教學設計案例研究[D].貴州師范大學,2018.
[5]劉冬艷.用數學建模構架課堂教學——“用一次函數解決問題”的課例分析與思考[J].初中數學教與學,2017(24).
[6]王玲燕.數形比對:函數性質探索的一條有效路徑——以人教版八年級下冊“一次函數的圖像及性質”的教學為例[J].中學數學,2017(22).
[7]楊文春.初中數學一次函數教學設計分析[J].數學學習與研究,2017(21).

