高斯消元法的教學創新與實踐

何章鳴 馬正芳

摘要：在高斯消元法教學中有一個怪現象：很多學員“講解快懂，做題快懵”。作者查閱國內外經典教材中高斯消元法講義后，發現導致上述現象的關鍵原因是：傳統解法“消元一回代一寫解”的步驟指代不清。在信息時代背景下，文章提出了“提取一變換一還原一移項一補齊”五步變換法，該方法更具體、更規范。結合數學軟件MATLAB將該方法付諸教學實踐，結果表明新方法過程具體、操作性強，可有效提高學員的學習效率。

關鍵詞：課程設置;教學創新;線性代數;高斯消元法;數學軟件

中圖分類號：G642.3 文獻標識碼：A 收稿日期：2019-06-04 文章編號：1674-120X（2019） 29-0104-02

一、引言

線性代數以向量、線性空間、線性變換和線性方程組等為對象，研究秩的等價不變性、特征值的相似不變性和慣性數的合同不變性，被廣泛地應用于自然科學和社會科學中。在線性代數教材[1][2]的內容組織架構中，線性方程組是各章節的樞紐工具。因而，線性代數關注點可歸結為兩個方面：第一，回答線性方程解的唯一性、存在性和結構性問題;第二，相似性和二次型可以看成方程組的應用。高斯消元法（Gaussian Elimination）印證了線性方程組和線性代數的實用性。[3]查閱國外經典教材[4]和國內教材可發現高斯消元法解線性方程組的主要工作是對增廣矩陣（Augmented Matrix）進行初等行變換，常把高斯消元法分解為三個步驟：步驟一，消元（Variable Elimination）：把增廣矩陣化為行階梯形，如果最后一個階梯的非零元素出現在最后，則方程組無解，否則方程有解;步驟二，回代（BackSubstitution）：在有解的情況下把行階梯形化為最簡行階梯形;步驟三，寫解（Write Solution）：把最簡行階梯形還原為同解方程組，求出所有解。

上面的解題步驟存在三個問題：問題一：步驟一忽略了消元前的增廣矩陣的提取過程，容易導致學員解題開端困難;問題二：步驟一和步驟二界線模糊，未考慮到常用數學軟件MATLAB并沒有行階梯形對應的命令。因為行階梯形 “不唯一”，容易導致學員解題不規范、易出錯;問題三：步驟三中“求出所有解”指代不清，隱藏大量細節步驟，容易導致學員解題丟三落四、得分率低。下面將進一步分析傳統高斯消元法的問題，最后給出對應的解決方案。

二、問題分析與解決方案

（一）問題分析

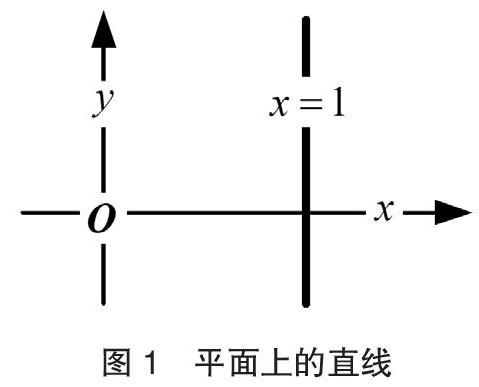
問題一：傳統方法忽略了增廣矩陣提取過程。例如，如圖1所示，二維平面上的一條直線的方程為。1。該方程非常簡單，而它的增廣矩陣并不是顯而易見的。教學實踐中發現，大量學員提取出錯誤的增廣矩陣，例如提取的增廣矩陣為[A，b]=[1，1]。經分析，原因可歸納為兩個方面：第一，自以為直線方程x=1是一維空間，其實該直線不經過零點，并不能構成線性空間，其實，該直線只是二維平面{[x，y]|x， y是實數}的一個子集，可表示為{[1，y]|y是實數};第二，方程x=1省略了0和1，實際上這是不規范的寫作習慣，容易導致提取出錯誤的增廣矩陣。實際上，x=1的完整式為1*x+0*y=1。對應的，增廣矩陣為[A，b]=[1，0， 1]。

問題二：傳統高斯消元法中，變換過程被分解為“消元”和“回代”兩部分。但是由于行階梯形不唯一，導致“消元”過程指代不清，不同學員獲得的行階梯形就不同，因而很難跟蹤和判斷答案是否正確。把“消元”和“回代”合二為一是必要的，即用“變換”直接獲得最簡行階梯形，原因有兩個：第一，最簡行階梯形是唯一的，學員能夠清晰地跟蹤和判斷答案是否正確，“一桿到底”更符合多數人的解題心理。行階梯形只是一個中間過程，不需要跟蹤其正確性。正因如此MATLAB和MATHMATICA沒有求解階梯形的命令。第二，合二為一后，規則簡單，容易上手，更符合信息時代背景。實際上MATLAB存在最簡行階梯形的命令，即RREF，為Reduce Row Echelon Form的縮寫。傳統的“消元”和“回代”的劃分方法符合計算機資源匱乏的手算時代。盡管行階梯形不唯一，但是若能提前判斷方程沒有解，則沒有必要將增廣矩陣化簡為最簡行階梯形，這樣就可以節約少量計算機資源。在信息時代背景下，教學計算機的計算性能冗余，筆者認為“規則簡單，機器判別”比“節約少量日算資源”更加可取。

問題三：傳統方法的“寫解”非常籠統，過程任務指代不清，學員無法理解其中的內涵，在解題時不知如何下手。實際上，“寫解”需要規范地分解為三個步驟：第一，把最簡行階梯形還原為線性方程組，“還原”是“提取”的逆過程，提取和還原構成了線性方程組求解的一個閉環;第二，移項：非階梯元所對應的變量就是自由變量，將自由變量移到方程組的右邊，即用自由變量表示非自由變量;第三，補齊：把自由變量代表的恒等式補齊。“補齊”是“省略”的逆過程，此時非齊次方程組的特解和導出組的基礎解系已經出現。

（二）解決方案

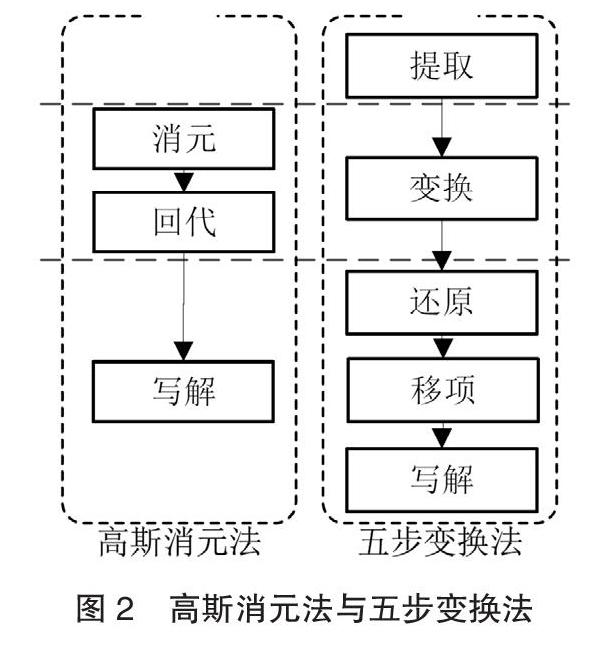
基于上述分析，提出過程規范的、操作性更強的、更適合教員教學和學員解題的線性方程組解法，所示，該方法包含“提取一變換一還原一移項一補齊”五個步驟，因此又稱該方法為“五步變換法”。

圖2刻畫了傳統高斯消元法與五步變換法的對應關系，區別有三個方面：第一，增加了“提取”過程。第二，將“消元”和“回代”合并為“變換”。第三，將“寫解”劃分為 “還原”“移項”“補齊”。

接下來，用“五步變換法”求解二維平面上的直線方程x=1。步驟一，提取：從x=1提取出增廣矩陣，得[A，b]=[1，0，1];步驟二，變換：將增廣矩陣變換為最簡行階梯形，[A，b]=[1， 0， 1]本身是最簡行階梯形”y自由變量，x為非自由變量，rank[A，b]=rankA=1，故方程有解;步驟三，還原：將最簡行階梯形還原為階梯方程組，得1*x+0*y=1;步驟四，移項：將自由變量移到方程右邊，得1*x=1+0*y;步驟五，補齊：將自由變量恒等式補齊，得到線性方程組的規范答案1*x=1+0*y， y=0+1*y，即[x，y]=[1，0]+y[0，1]。