幼師數學教學中培養學生空間思維能力的研究
于萍
摘要:空間思維能力是一種普遍的思維能力,空間思維由三大要素組成:空間概念、呈現工具、推理過程。發展學生的空間思維能力,可以從理解空間意義,利用空間的各種性質形成問題,尋找答案,并呈現解決方案入手。幼師的立體幾何教學,能培養學生的空間思維能力并為他們未來的幼兒園教學打好基礎。當前,部分幼師學生的空間思維能力較低。通過引導學生觀察、討論、講解、畫圖、制作幾何教具、強化習題訓練等形式,能全方位提升學生的空間思維能力。
關鍵詞:幼師生;數學教學;空間思維能力
空間思維也稱“多元思維”“全方位思維”“整體思維”,是指跳出點、線、面的限制,能從上、下、左、右,四面八方去思考問題的思維方式,也就是要“立起來思考”。空間思維能力不但對一個人的日常生活非常重要,也與其日后科學、技術、工程和數學領域的學習緊密聯系。
幼兒教育是國民教育的基礎,幼兒科學素養的形成與發展需要與之相匹配的教育。幼兒教師的空間思維能力直接影響到幼兒的空間思維能力的高低。數學教材中立體幾何教學是培養學生空間思維能力的最有效途徑。
教學中,我們要通過引導學生親身經歷、實際操作、語言表述、簡單推理論證等方法來達到提升空間思維能力的目的。為此,我對學前教育專業“空間幾何圖形”教學內容進入了深度挖掘,結合幼師學生的特點,采取多種教學方式,注重激發學生的學習興趣,讓學生參與到課堂教學的各個環節;注重引導學生通過探究活動,得出問題的答案。通過觀察、討論、講解、畫圖、制作幾何教具等多種形式,全方位提升學生的空間思維能力。
一、強化概念教學,借助直觀教具建立空間概念
基本概念是學生建立空間思維的基礎,在教學中要加強基本概念的教學。教師要幫助學生理解空間概念的定義、定理、性質和一些推理的結論。幼師學生雖然學習過平面幾何,具備了一定的圖形知識,但其思維從二維平面圖形向三維立體圖形的轉化仍有困難。要想使學生的空間思維方式順利地完成由平面到立體的轉化,教學中教師要依據學生的認知規律,由具體到抽象地設計教學過程。可以發給學生直觀的教具,引導學生去觀察、觸摸、測量幾何體。同時,引導學生通過直觀教具的幫助,分清實物中線與線之間的關系、線與面的關系、面與面之間的關系。也可以引導學生自制學具,如準備一些牙簽、橡皮泥和硬紙板等,把牙簽當作直線,把硬紙板當作平面,用橡皮泥固定住牙簽,做出研究問題中需要的各種幾何體。在探究的過程中,能增強學生的信心、激發學習數學的興趣、逐步建立空間概念,提升空間思維能力。
二、加強與實際生活的聯系,感知空間觀念
空間想象能力的基礎是空間觀念,而空間觀念的來源是我們對現實世界的直接感知與認識。空間幾何體是日常生活中很多物體的幾何模型,教學中與日常生活相聯系會增加幾何體的直觀性,降低抽象性。
教師可以充分利用教室這個立體空間,引導學生分析教室內的燈、墻面、黑板面之間的位置關系。還可以設置與生活相關的問題讓學生探究,給予學生動手操作實踐的機會。如在學習“長方體的對角線”時,我設置了如下問題:操場上有一堆磚,現在只有一把直尺,你能把其中一塊磚的對角線的長度量出來嗎?完成這道題,需要學生會找出長方體的對角線是哪條線段。在無法直接測量的情況下,要發揮空間想象力,借助“操場上有一堆磚”來達到解題的目的。(解這道題只需要把兩塊磚并排放在地面上,然后拿走其中的一塊,刻畫其在地面上留下痕跡,然后用直尺量就可以了)
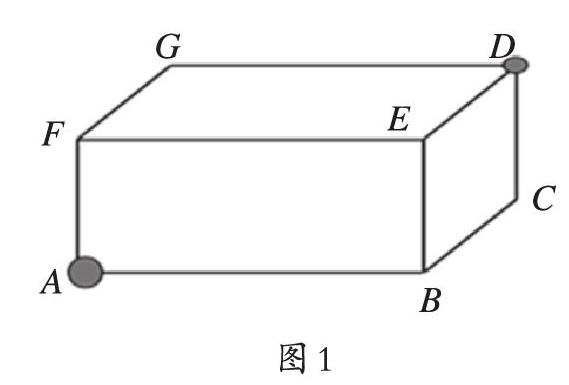
在學習幾何體平面展開圖時,可以設置問題: 一個長方形的木塊(如圖1), 已知AB=6cm,BC=5cm,BE=4cm。一只蜘蛛在長方體的頂點A處,一只蚊子在另一個頂點D處,問蜘蛛沿怎樣的路線爬行,才能最快抓住蚊子?
解這道題,需要學生把幾何體的平面展開圖畫出來,根據兩點之間距離最短畫線,計算連結A、D兩點的最短線段的長度。
三、熟記畫圖規則,增強畫圖、識圖的意識
畫圖和識圖是學好立體幾何的基礎,也是教學的重點和難點。教師要重點研究在學習立體幾何過程中學生的圖形感知、識別障礙,幫助他們克服困難。
在幾何體部分的教學中,需要學生掌握兩種圖形的畫法,一是幾何體的直觀圖,二是幾何體的表面展開圖。通過畫直觀圖,可以把生活中的幾何體在紙上直觀地呈現出來。畫直觀圖的目的是通過畫圖的訓練,使學生達到在觀看幾何體的直觀圖時,能把幾何體“立起來”,能看清幾何體的點、線、面的各種關系。這也是培養學生空間思維能力的重要環節。 教學中,教師要幫助學生掌握畫圖規則,弄清畫法原理,加大訓練力度,增強作圖意識。
通過畫幾何體的表面展開圖的學習,學生可以掌握如何把一個幾何體的各個面依次、連續地展開,并畫在同一個平面內的方法。在學習過程中,學生對幾何體的各個面之間的位置關系會有更深刻的認識,這有助于提升他們的空間想象力。同時,學生掌握了這種畫圖的方法,就可以根據需要,畫出幾何體的平面展開圖,然后經折疊、粘貼,制成立體幾何教具、學具。
四、設計趣味習題,提升空間思維能力
幼兒園中的數學活動帶有趣味性,幼師學生也特別喜歡趣味性高的習題。每當做趣味數學題時,很多學生往往會忘掉對數學的恐懼心理,并積極地投入到探究之中。
在提高學生空間思維能力的數學活動中,經常會出現“折疊”“旋轉形狀”“切割”等主題。這些活動的設計和教學,需要較高的空間思維能力。很多學生的空間思維能力經過一段的學習,雖然得到了一定的提升,但是仍缺乏解決問題的變通和靈活性。為使他們在提升空間思維能力的同時,體會幼兒園數學科學活動的特點,在教學中我選取了最具有代表性、最簡單的幾何體——正方體來設計了四個問題。
通過一系列由淺入深的正方體趣味習題,使學生在平面圖形與立體圖形的轉換訓練中,快速提升了空間思維能力。
問題一:你能畫出幾個正方體的平面展開圖?
學生畫圖,教師匯總,一共得出11種不同的畫法。教師引導學生歸納這11種展開圖的特點,總結規律,幫助記憶。目的是為后面探究正方體與其表面展開圖的對應關系打下基礎,提升學生畫正方體表面展開圖的能力。
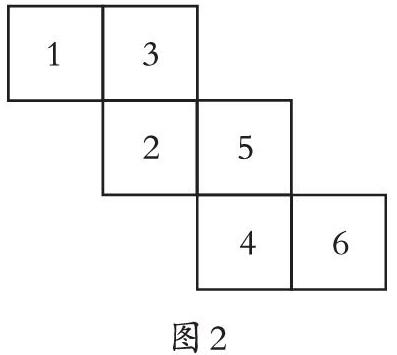
問題二:圖2中給出了正方體的平面展開圖,你能找出這個正方體中分別與數字“ 1 ”“2”“3”相對的面是哪些面嗎?
學生通過探究,找出了與數字 “ 1 ”“2”“3”相對的面分別是數字“5”“6”“4”,然后教師要總結找相對面的規律和方法。通過這道題的訓練,提升了學生把正方體的表面展開圖抽象轉化成正方體的能力。
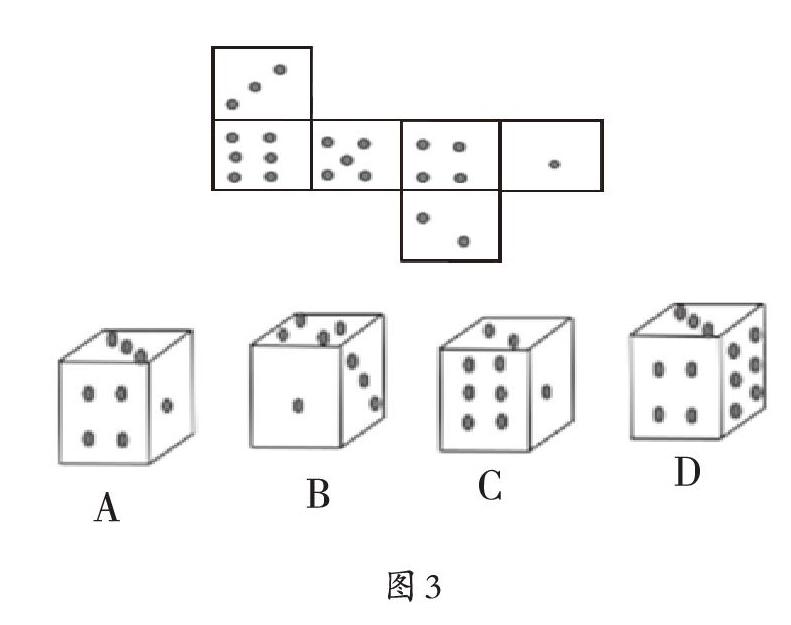
問題三:觀察給定的正方體展開圖,在下面四個選項中選出哪個幾何體不能被它折出?(如圖3)
這道題是在前兩道題的基礎上完成,需要較高的抽象思維能力。學生只有在頭腦中經歷一次把平面圖形“立起來”的過程,利用找立方體相對面的方法、抽象思考每個面上“圓點”的擺放位置,才能給出問題的答案。在此過程中,學生空間想象力又得到一次提升。
問題四:把一個棱長為3厘米的正方體表面涂滿紅色,然后切成邊長為1厘米的小正方體。請問:
(1)至少需要切幾刀?
(2)最多能得到多少個邊長為1cm的正方體?
(3)有多少個正方體三個面涂有紅色?
(4)有多少個正方體二個面涂有紅色?
(5)有多少個正方體一個面涂有紅色?
(6)有多少個正方體六個面都沒涂色?
這是一道立體圖形空間切割題,需要更高的空間想象和抽象思維能力。可以鼓勵學生合作探究,給出問題的答案。
通過這一系列習題的訓練,學生不但掌握了立體幾何的基本知識,還提升了邏輯思維能力、空間想象能力、畫圖能力、計算能力、分析問題和解決問題的能力,為幼兒園數學科學活動的創編打下了良好的基礎。
五、制作幾何玩、教具,適應幼教需要
“玩、教具設計與制作”是幼師學生必修的教育技能之一。幼兒園幾何體的教學中需要大量的幾何體教具和學具。在幼師立體幾何教學中,教師應鼓勵學生利用所學的幾何體平面展開圖知識制作學具、教具。學生掌握了這一技能,才能適應幼兒園教學的需要。
在學生制作教具之前,教師應教給學生掌握多種幾何體表面展開圖的畫法,如柱體、錐體、臺體以及五種正多面體的畫法。實踐中,可以讓學生自由選取所要制作的種類。教師可以給學生展示上一屆學生的優秀作品,使他們開闊眼界,打開思路,制作出更好的玩、教具。作品可以是一個幾何體,也可以是一些不同的幾何體組成的場景。為進一步提升學生的參與興趣,我們還舉行了全校的制作幾何體教具大賽,學生參與的積極性很高。
參考文獻:
[1]王祥.我們要學習“有用”的數學——淺談立體幾何主題活動教學對幼師生的影響[J]. 數學學習與研究,2014(3).
[2]吳偉.高等幼兒師范學校立體幾何教學的探索 [J].學園,2015(32).
(責任編輯:楊強)

