立足生活常識 導向核心素養

楊亞軍

【摘 要】 近兩年，高考試題已清晰地從圍繞知識、能力的命題向素養立意下的圍繞育人目標的命題進行轉變。如何在課堂教學及日常訓練中落實，這是一個全新的課題。本文立足生活常識，從設計編制培養和發展學生核心素養的“問題”這個角度做了一點探索與實踐。

【關鍵詞】 核心素養? 數學抽象? 幾何模型

新課程標準從政策層面、高考從評價選拔層面都要求教育要指向學生的核心素養，要注意發展學生的高階思維能力。這就要求我們要盡快從過去的一味訓練學生“解題”，轉向啟發、指導學生學會“解決問題”。要做好這個轉變，對我們教師而言，很重要的一點就是要學會立足生活、立足學生實際，給學生設計或編制有價值的“問題”。

“山路彎彎”，不論是“千峰疊翠萬重煙，清風索繞十二盤”的青海十二盤坡，還是318線上的怒江七十二道拐，這些盤山公路之所以有這么多彎、這么多拐，這其中是有科學道理的。下面，我就立足這一生活中的現象和常識，在學生學習了空間角的計算之后，給學生提出這樣一個對學生而言既熟悉又陌生的“問題”——同學們試著應用我們所擁有的知識與方法，重點從數學的角度，給出“在陡峭的山坡上修公路，為何都修成了盤山公路”的道理之所在（記為“探索性問題”）。

學生幾乎都能說出修成盤山公路，路就不太陡，車就容易上去。還有學生可能會從機動車爬坡的安全性與能力，甚至有學生可能從道路交通設計等方面，搜索到修路時對路面所在斜坡坡度（或坡比）最大值的政策規定（如不同車速的公路，車速由高到低其道路的最大坡度從3%到10%，積雪寒冷地區的最大坡度推薦值不大于6%）。

在此基礎上，引導學生挖掘此問題的本質原因：為什么修成盤山路后路面的坡度就能變小？在實際施工中，如何根據坡度的限定值，規劃路線呢？（初步“具體化了的問題”）。教師適時、恰當地引導、啟發學生，設法把這個問題理想化、數學化、模型化。路要修在山坡上，山坡很陡峭。從數學的角度，這里涉及到數學中的什么角呢？——二面角——水平面與山坡的坡面所成的二面角。若咱們再把山路截取一個片段，山路在我們的眼中就不是彎的，而是直的了。自然地，學生會想到，把山路的坡角看成直線與水平面所成的線面角。至此，這個“具體化了的問題”通過理想化，與學生熟悉的立體幾何中的二面角、線面角建立了聯系。這時，剛才的“問題”可以進一步數學化，成為一道“具體的數學題”——已知二面角的大小，在其中一個半平面內確定一條與二面角的棱相交的直線，使得該直線與另一個半平面所成的角為給定的值。

至此，實現了把“實際問題”數學化，這一過程中有分析判斷，有數學抽象。

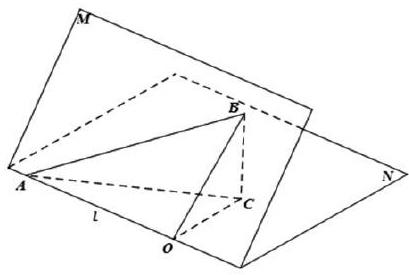
接下來，對大多數學生而言，應該是輕車熟路了。在立體幾何中，我們有研究解決這種二面角與線面角的幾何模型。如圖，在二面角M-l-N中，用半平面M代表山坡的一段坡面，用半平面N代表水平面，AB代表山路的一個片段。在圖中作BC⊥平面N于點C，作CO⊥l于點O，連結BO，則BO⊥l. 從而∠BOC是二面角M-l-N的平面角，∠BOC的大小就表示該段山坡的陡峭程度.而∠BAC是直線AB與平面N所成的線面角，其大小就表示這段山路的坡角大小。

顯然∠BAC<∠BOC（∵BA>BO），這就是為什么要修盤山路的數學解釋。

事實上，這里用到了立體幾何中一個很重要的模型：四個面都是直角三角形的四面體（三棱錐）。這個模型可以幫助解釋“直線與它在平面內的射影所成的角是該直線與平面內所有直線所成的角中最小的”（∵cos∠BAO=cos∠BAC·cos∠OAC，這就是特殊三面角公式，它給出了線面角定義的合理性和科學性：為什么把一條直線與它在平面內的射影所成的角定義為該直線與該平面所成的角——該角的最小性、唯一性）。這一過程中有模型，有推理，也有計算。

教師亦可在這兒提一下一般三面角公式，提醒有興趣的同學下去研究或查閱有關資料，了解其具體表達式及含義。

上面的模型（圖中的四面體BAOC）也是研究正棱錐的“標本”，它包含了正棱錐幾乎所有的基本量及其關系。視點B為正棱錐的頂點，則點C為正棱錐底面正多邊形的中心，從而BA為正棱錐的側棱，BO為正棱錐的斜高，AO為正棱錐底面正多邊形一條邊長的一半。

通過這樣的“問題解決”，學生不僅能深刻理解線面角與二面角的概念及其計算，還能應用所學數學知識，研究解釋生活中現象。在此過程中，學生對數學的應用價值也有了更深入地認識，同時也較好地發展了學生的數學核心素養（數學抽象、數學推理、數學建模、數學計算等）。自然地，這也是訓練、發展學生分析、評價、創造這些高階思維的一個很好的素材。

參考文獻

[1] 普通高中數學課程標準（2017年版）.中華人民共和國教育部制定.人民教育出版社，2018.1：4-8.

[2] 葛軍.新編高中數學奧賽指導.南京師范大學出版社，2010.6：245-246.