數(shù)形結(jié)合思想中“以形助數(shù)”在小學(xué)數(shù)學(xué)教學(xué)中的運(yùn)用探究
梁錦標(biāo)


摘要:在小學(xué)數(shù)學(xué)教學(xué)中,運(yùn)用數(shù)形結(jié)合思想進(jìn)行教學(xué),有助于小學(xué)生更好地學(xué)習(xí),促進(jìn)學(xué)生的有意義識(shí)記,順利解決數(shù)學(xué)問題。“以形助數(shù)”作為數(shù)形結(jié)合思想的一種,在小學(xué)數(shù)學(xué)教材中的運(yùn)用并不鮮見,無論是數(shù)與代數(shù)、圖形與幾何還是統(tǒng)計(jì)與概率、綜合與實(shí)踐等教學(xué)內(nèi)容,都能運(yùn)用“以形助數(shù)”思想輔助教學(xué)。
關(guān)鍵詞:小學(xué)數(shù)學(xué);數(shù)形結(jié)合;以形助數(shù)
一、數(shù)形結(jié)合思想的內(nèi)涵及其在小學(xué)數(shù)學(xué)教學(xué)中的運(yùn)用意義
在課堂教學(xué)中,教師要堅(jiān)持以學(xué)生為主體,教師為主導(dǎo),在講授知識(shí)的同時(shí)更要充分發(fā)揮學(xué)生的主觀能動(dòng)性,使得學(xué)生在思考與探究、合作與交流的過程中,能夠形成良好的數(shù)學(xué)思維、獲得基本的數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)、理解和掌握基本的數(shù)學(xué)知識(shí)與技能。這是《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2011年版)》(下文簡稱《課標(biāo)》)所體現(xiàn)的課程理念,除此之外,《課標(biāo)》在課程總目標(biāo)中提出:“通過義務(wù)教育階段的數(shù)學(xué)學(xué)習(xí),學(xué)生能獲得適應(yīng)社會(huì)生活和進(jìn)一步發(fā)展所必需的數(shù)學(xué)的基礎(chǔ)知識(shí)、基本技能、基本思想、基本活動(dòng)經(jīng)驗(yàn)。”由此可以看出,《課標(biāo)》從課程理念到課程目標(biāo),都強(qiáng)調(diào)數(shù)學(xué)教學(xué)并不是簡單地傳授相關(guān)數(shù)學(xué)知識(shí),它更注重于學(xué)生思維的鍛煉,講究培養(yǎng)學(xué)生的數(shù)學(xué)思想和引導(dǎo)學(xué)生掌握數(shù)學(xué)方法。
學(xué)生的心理發(fā)展具有一定的方向性和順序性,階段與階段之間是不可逾越的。處于學(xué)齡初期的學(xué)生以具體形象思維為主,到了四年級(jí),學(xué)生的思維雖逐漸以抽象邏輯思維為主導(dǎo),但是,其抽象邏輯思維仍然需要具體形象思維的支撐;而總的來說,數(shù)學(xué)這一門課程的知識(shí)較為抽象。這樣,數(shù)學(xué)課程知識(shí)的抽象性與小學(xué)生的具體形象思維就構(gòu)成了一對(duì)矛盾。如何解決這一矛盾,讓學(xué)生學(xué)習(xí)數(shù)學(xué)時(shí)不那么吃力?“數(shù)形結(jié)合思想”的運(yùn)用能有效解決這一現(xiàn)實(shí)問題,它能讓復(fù)雜的知識(shí)簡單化,讓抽象的知識(shí)形象化,促進(jìn)學(xué)生更好地理解問題表征,從而順利地解決數(shù)學(xué)問題。
數(shù)形結(jié)合一般包含“以數(shù)解形”“以形助數(shù)”兩個(gè)方面,是指將抽象的數(shù)量關(guān)系與直觀的圖形結(jié)構(gòu)巧妙地結(jié)合起來,達(dá)到抽象問題具體化、復(fù)雜問題簡單化,以實(shí)現(xiàn)優(yōu)化解題途徑的目的。
如何將數(shù)形結(jié)合思想滲透在小學(xué)數(shù)學(xué)教學(xué)中,以有效培養(yǎng)學(xué)生的數(shù)形結(jié)合思想,讓其自覺地運(yùn)用在數(shù)學(xué)問題解決中?筆者認(rèn)為,要達(dá)到這個(gè)目的,數(shù)學(xué)教師就必須將數(shù)形結(jié)合思想的運(yùn)用貫穿于教學(xué)的始終,無論是數(shù)與代數(shù)、圖形與幾何還是統(tǒng)計(jì)與概率、綜合與實(shí)踐等教學(xué)內(nèi)容,都要有意識(shí)地滲透數(shù)形結(jié)合思想。現(xiàn)筆者結(jié)合自身實(shí)踐,談?wù)勅绾螌?shù)形結(jié)合思想中的“以形助數(shù)”運(yùn)用在小學(xué)數(shù)學(xué)教學(xué)中。
二、數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的運(yùn)用
(一)數(shù)與代數(shù)
在四年級(jí)上冊(cè)第1課“大數(shù)的認(rèn)識(shí)”中的“1億有多大”的教學(xué)時(shí),若教師直接采用語言傳授的教學(xué)方法,則無法讓學(xué)生直觀地感受“1億”到底有多大。為此,筆者先把學(xué)生分成3組,第1組探究我校的課室一般能容納多少人,要容納1億個(gè)人需要多少間這樣的課室;第2組探究我們所用的一本數(shù)學(xué)教科書有多重,要有多少本這樣的數(shù)學(xué)教科書才能有1億克;第三組測(cè)量學(xué)校的升旗桿有多高,要有多少根這樣的升旗桿才能有1億米高。
任務(wù)分配下去后,學(xué)生饒有興趣地積極行動(dòng)起來。經(jīng)過探究合作與交流,第1組學(xué)生探究出1間課室約能容納100個(gè)人,需要100萬間課室才能容納完1億人;第2組學(xué)生測(cè)量出一本數(shù)學(xué)教科書大概150克,大約需要67萬本這樣的教科書才能達(dá)到1億克;第3組學(xué)生測(cè)量出學(xué)校的升旗桿為12米高,大約需要833萬根這樣的升旗桿才能有1億米高。看著這一組龐大的數(shù)據(jù),學(xué)生紛紛發(fā)出感嘆聲。
在活動(dòng)探究中,筆者利用“以形助數(shù)”的思想,巧妙地把抽象的大數(shù)“1億”轉(zhuǎn)換成具體的事物——課室、教科書、升旗桿。這樣一來,不但能順利地讓學(xué)生直觀感受“1億”這個(gè)數(shù)到底有多大,還能讓學(xué)生在探究過程中習(xí)得合作精神和實(shí)踐能力。
(二)圖形與幾何
五年級(jí)上冊(cè)第6課的教學(xué)內(nèi)容為“多邊形的面積”,主要涉及了平行四邊形、三角形、梯形以及組合圖形的面積計(jì)算。在實(shí)際教學(xué)過程中,筆者發(fā)現(xiàn),很多學(xué)生容易混淆面積公式,特別是教材安排了平行四邊形面積的內(nèi)容后緊跟著三角形面積的內(nèi)容,在做題的時(shí)候,學(xué)生要么忘記除以2,要么多了一個(gè)除以2。這就證明學(xué)生還未真正理解多邊形的面積公式,只是死記硬背。
平行四邊形的面積公式為S=ah,三角形的面積公式為S=ah÷2,為了讓學(xué)生牢牢掌握這兩個(gè)多邊形的面積公式,筆者借助圖形的分解,幫助學(xué)生理解平行四邊形與三角形之間的聯(lián)系。
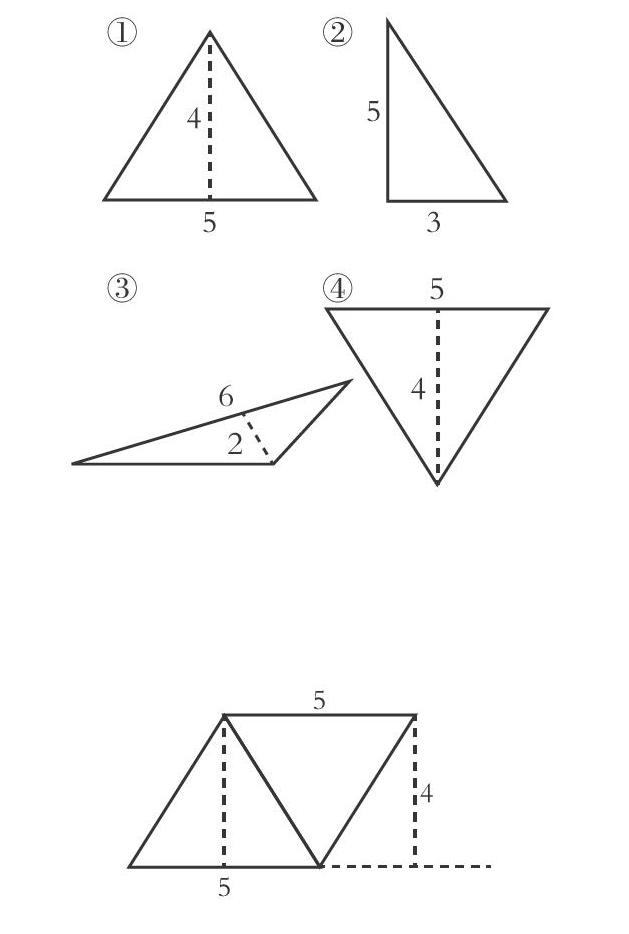
首先,筆者出示了四個(gè)三角形,并問學(xué)生:哪兩個(gè)三角形能拼成平行四邊形?這兩個(gè)三角形有什么關(guān)系?
學(xué)生很快就發(fā)現(xiàn)第1個(gè)和第4個(gè)三角形能拼成平行四邊形,而且這兩個(gè)三角形是完全相同的。
此時(shí),筆者追問:三角形的底和高與拼成的平行四邊形的底和高存在什么關(guān)系呢?每個(gè)三角形的面積與拼成的平行四邊形又有什么關(guān)系呢?學(xué)生也很快就能得出:拼出的平行四邊形的底和高等于三角形的底和高,每個(gè)三角形的面積等于平行四邊形面積的一半。最后,筆者做簡單的總結(jié):也就是說,三角形的面積=平行四邊形的面積÷2。
在這一教學(xué)過程中,筆者仍利用了“以形助數(shù)”的思想,借助圖形的分解與結(jié)合,讓學(xué)生理解為什么三角形的面積公式要除以2。經(jīng)歷了這一過程,學(xué)生便能對(duì)三角形面積公式進(jìn)行有意義的識(shí)記,有效地避免了與平行四邊形的面積公式相混淆。
(三)統(tǒng)計(jì)與概率
統(tǒng)計(jì)與概率這一教學(xué)內(nèi)容本身就是“以形助數(shù)”思想的體現(xiàn),如五年級(jí)下冊(cè)第7課“折線統(tǒng)計(jì)圖”這一教學(xué)內(nèi)容將復(fù)雜、變化的數(shù)字以折線圖的形式表現(xiàn)出來,能讓人直觀地看到數(shù)據(jù)的變化。如下圖,將2006年至2011年中國青少年機(jī)器人參賽隊(duì)伍做成折現(xiàn)統(tǒng)計(jì)圖,能直觀地獲取2007年參賽隊(duì)伍最少、2011年參賽隊(duì)伍最少,從2009年開始參賽隊(duì)伍逐年增多等信息。
(四)綜合與實(shí)踐
部編版數(shù)學(xué)教材從二年級(jí)開始增加了“數(shù)學(xué)廣角”模塊,也就是“綜合與實(shí)踐”這一內(nèi)容,目的在于讓學(xué)生認(rèn)識(shí)到,實(shí)際生活中蘊(yùn)藏著豐富的數(shù)學(xué)知識(shí),引導(dǎo)學(xué)生積極地嘗試從數(shù)學(xué)的角度出發(fā),運(yùn)用所學(xué)的數(shù)學(xué)知識(shí)以及數(shù)學(xué)方法解決在實(shí)際生活中遇到的問題。
五年級(jí)上冊(cè)的數(shù)學(xué)廣角內(nèi)容為“植樹問題”。植樹問題主要涉及三種植樹方法:兩端都植樹、一端植樹、兩端都不植樹。不同的植樹方法有不同的計(jì)算方法,為了讓學(xué)生理解三種不同的植樹方法并尋得其中規(guī)律,筆者結(jié)合圖形進(jìn)行授課。
首先,筆者出示了下圖,并要求學(xué)生根據(jù)圖片完成下表。
完成后,筆者提問學(xué)生是否發(fā)現(xiàn)什么規(guī)律。學(xué)生很快便能發(fā)現(xiàn),兩端植樹的方法,間隔數(shù)比棵樹少1;一端植樹的方法,間隔數(shù)與棵樹相等;兩端不植樹的方法,間隔數(shù)比棵樹多1。
最后,筆者與學(xué)生一起總結(jié)“植樹問題”的規(guī)律:兩端都植樹時(shí),棵樹=距離÷間隔數(shù)+1;一端植樹時(shí),棵樹=距離÷間隔數(shù);兩端都不植樹時(shí),棵樹=距離÷間隔數(shù)一1。
在這一教學(xué)中,教師并不是生硬地將植樹問題的規(guī)律直接灌輸給學(xué)生,而是結(jié)合圖畫,逐步引導(dǎo)學(xué)生發(fā)現(xiàn)其中規(guī)律,加深了學(xué)生對(duì)植樹問題的理解。
美國圖論學(xué)者哈里認(rèn)為:“千言萬語不如一張圖。”華羅庚說:“數(shù)與形,本是相倚依,焉能分作兩邊飛。數(shù)無形時(shí)少直覺,形少數(shù)時(shí)難入微。數(shù)形結(jié)合百般好,隔離分家萬事非;切莫忘,幾何代數(shù)統(tǒng)一體,永遠(yuǎn)聯(lián)系,切莫分離!”從這可見,在小學(xué)數(shù)學(xué)教學(xué)中,滲透“以形助數(shù)”的思想,有助于以具體形象思維為主的小學(xué)生更好地理解相對(duì)抽象的數(shù)學(xué)知識(shí),鞏固教學(xué)效果。

