熟識幾何基本模型實現數學解題化繁為簡研究

胡清山

摘 要：“反A型”旋轉相似直角三角形模型在近幾年的中考題中常常出現，并經過中考命題專家的變式演繹，出現了常考常新的情況。為了更好地解答這種模型的幾何題，教師應引導學生注意觀察圖形和分析圖形，學會從復雜的圖形中分離出這種幾何基本模型，理解這種基本的幾何模型所蘊含的基本結論并掌握基本的解法，提高解題能力。

關鍵詞：數學教學;解題;幾何模型;靈活應用

中圖分類號：G633.6 文獻標志碼：A文章編號：1008-3561（2020）15-0084-04

旋轉變換是初中幾何的一個重要考點，而相似是中考的核心考點，相似與旋轉有機結合成為近年來中考的一大核心模塊，也是考查學生的幾何分析能力的重要載體，使幾何綜合題難度變大。要突破這個難點，不僅要求學生牢固掌握旋轉變換的性質、相似三角形的性質和基本的判定方法，而且要求學生熟識一些基本的圖形模型。為此，教師要在課堂教學中有意識地對一些基本的幾何圖形模型進行提煉和識別，并對這些基本的圖形模型的應用進行專題訓練，以提高學生解決幾何綜合題的能力。本文重點介紹如何應用“反A型”旋轉相似直角三角形模型中的兩個基本結論迅速解題，讓學生充分地體會到幾何基本圖形在解決幾何綜合題時可起化繁為簡、化難為易的作用。

一、模型感知

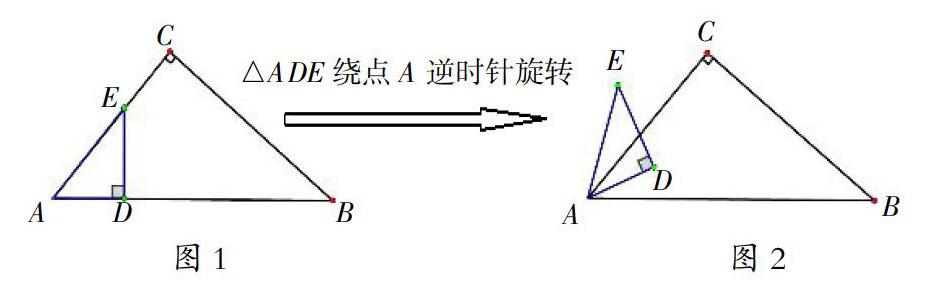
“反A型”旋轉相似直角三角形模型：如圖1，△ACB和△ADE都是Rt△，且∠ACB=∠ADE=90°。若點E、D分別落在邊AC、AB上，△ABC固定不動，將△ADE繞點A逆時針旋轉，如圖2。把旋轉中的Rt△ADE和Rt△ABC組成的幾何模型稱為“反A型”旋轉相似直角三角形模型。（教師用幾何畫板演示旋轉）

二、基本圖形的結論探究

1.特殊發現

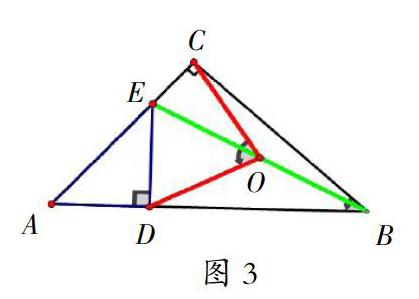
如圖3，△ACB和△ADE都是Rt△，且∠ACB=∠ADE=90°。若點E、D分別落在邊AC、AB上，連接BE，點O為BE的中點，連接OC、OD，試判斷線段OC和OD之間的數量關系以及∠COD和∠ABC之間的數量關系，并加以證明。教師引導學生獨立思考：根據特殊情況中的條件發現結論，并思考如何證明結論。

答：OC=OD，∠COD=2∠ABC。證明：因為∠ADE=∠ACB=90°，O為BE的中點，所以OC=OD=OB=OE=1/2BE。所以點B、C、E、D四點在以點O為圓心、OC為直徑的圓上。再根據圓周角定理易得：∠COD=2∠ABC。

利用“直角三角形斜邊上的中線等于斜邊上的一半”得到OC=1/2BE和OD=1/2BE，進而證得OC=OD。利用“等邊對等角”以及“三角形的一個外角等于與它不相鄰的兩個內角的和”這兩個性質得到“等腰三角形與頂角相鄰的外角等于底角的兩倍”即∠COE=

2∠OBC，∠DOE=2∠OBD，進而證得∠COD=2∠ABC。利用對角互補的四邊形的四個頂點共圓，再利用“同弧所對的圓周角等于它所對的圓心角的一半”證得∠COD=2∠ABC。

設計意圖：教師通過對特殊情況的觀察和探究，培養學生的觀察能力以及簡單的幾何問題的分析能力和推理能力，為接下來的一般情況的探究做鋪墊。

2.深化探究

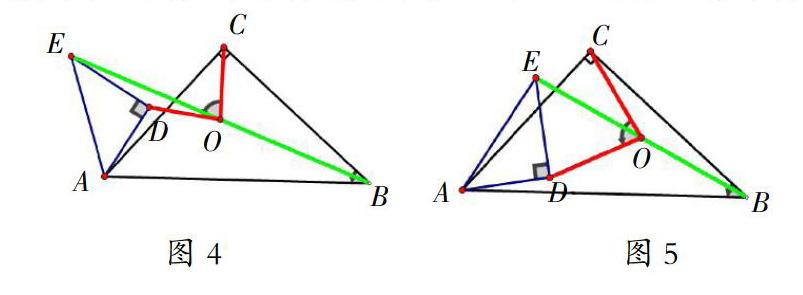
圖3中Rt△ABC固定不動，將Rt△ADE繞點A逆時針旋轉任意的角度α（如圖4或圖5），請你觀察、思考、分析、判斷上述結論是否成立，并證明你的判斷。

活動1：教師借助幾何畫板演示Rt△ADE繞點A旋轉過程，并讓學生觀察Rt△ADE在旋轉過程線段OC和OD之間的數量關系以及∠COD和∠ABC之間的數量關系，并做出猜想判斷。活動2：教師用幾何畫板演示Rt△ADE繞點A旋轉到不同位置，并同時給出在某一位置線段OC和OD的度量值以及∠COD和∠ABC的度量值，讓學生判斷一下自己的猜想是否正確。

設計意圖：教師有意識地引導學生進行幾何基本圖形的識別，并總結出蘊含在基本幾何圖形中的基本結論，有助于培養學生的觀察能力和總結歸納能力。

3.證法點撥

提問1：證明“有公共端點的兩條線段相等”有哪些常用的方法？（學生獨立思考后進行討論交流，舉手回答，教師補充說明）①利用“等角對等邊”這一性質來證明。②利用“全等三角形的對應邊相等”這一性質來證明。③利用“直角三角形斜邊上的中線等于斜邊的一半”這一性質來證明。

提問2：與線段中點有關的引輔助線方法有哪些？①取與已知線段有公共端點的線段中點（或倍長與已知線段有公共端點的線段）——構造中位線。②構造直角三角形斜邊上的中線。③有以線段中點為端點的線段時，常倍長此線段，構造“X型”的全等三角形。

設計意圖：考慮到這兩個結論證明的困難性，教師借助兩個問題引發學生思考，教授學生解決此類問題的基本方法，使不同水平的學生有不同的發現，加深學生對一些幾何基本模型以及基本方法的理解，也為反“A”型旋轉相似直角三角形模型的基本結論的證明做好鋪墊。

提問3：請學生們用幾何的方法證明“OC=OD，∠COD=2∠ABC”。

4.證法展示和評析

證法一：如圖6，分別取AB、AE的中點M、N，連接OM、ON、CM、DN，易證四邊形OMAN是平行四邊形，所以∠OMA=∠ONA。根據“三角形的中位線定理”和“直角三角形斜邊上的中線等于斜邊的一半”可得CM=ON，OM=DN。易證：△AMC∽△ADN，所以∠AMC=∠DNA，于是可得∠OMC=∠OND，進而可證△CMO≌△DNO，所以OC=OD，∠OCM=∠DON。因為ON∥AB，所以∠MHO=∠DON。根據等量代換，有∠MHO=∠OCM。因為∠OGC=∠HGM，所以∠COD=∠AMC。因為∠AMC=2∠ABC，所以∠CON=2∠ABC。這種證法是分別取兩Rt△斜邊的中點，構造三角形中位線和直角三角形斜邊上的中線，進而構造全等三角形;而證明角與角的關系主要是通過“8”字型來導角。

證法二：如圖7，延長CO至點F，使得OF=OC，連接CD、DF、EF，易證△EOF≌△BOC，所以EF=BC，∠FEB=∠EBC，所以EF∥BC，所以∠AMF=∠ACB=90°。進而可證∠AME=∠ADE=90°，因為∠ENM=∠AND，所以∠DEF=∠DAC。易證△DAC∽△DEF，所以=，∠ADC=∠EDF，可推得∠CDF=∠ADE。又因為=，即

tan∠CFD=tan∠ABC，所以∠CFD=∠ABC，易證∠COD=2∠CFD，所以∠COD= 2∠ABC。這種證法是采用倍長兩線段中的一條的方法，構造“A型”旋轉相似模型和直角三角形斜邊上的中線。

證法三：如圖8，延長BC至F，使CF=BC;延長ED至G，使DG=DE;連接EF、AF、BG、AG，易證：AF=AB，AG=AE，△AEG∽△FAB。所以∠FAB=∠EAG，可得∠EAF=∠GAB，進而可證△AEF≌△AGB。所以EF=BG，∠AFE=∠ABG，易得OC=1/2EF，OD=1/2BG ，所以OC=OD。因為AF=AB，所以∠AFC=∠ABC，所以∠COD=∠EOD+∠COE=∠ABG+∠ABE+∠OBC+∠OCB=∠AFE+∠ABC+∠CFE=∠AFC+∠ABC=2∠ABC。這種證法是采用分別倍長兩Rt△無公共端點的直角邊的方法，構造線段的垂直平分線、三角形中位線以及“手拉手”相似模型，并利用“手拉手”相似模型的“一拖二”性質來證明△AEF≌△AGB。（“手拉手”相似三角形會衍生出“手拉手”相似三角形;當“手拉手”相似的兩個三角形是等腰三角形時，一定會衍生出“手拉手”全等三角形，把這樣的性質稱為“手拉手”相似模型的“一拖二”性質）而證明角與角的關系主要是利用兩直線平行，同位角相等、三角形外角的性質以及等邊對等角等性質來導角。

三、模型應用

1.直接應用基本圖形模型解題

當幾何圖形中出現“反A型”旋轉相似直角三角形的基本圖形模型時，可直接利用模型及模型所蘊含的基本結論的證明方法高效地解決問題。例題：在Rt△ACB和Rt△AEF中，∠ACB=∠AEF=90°，若點P是BF的中點，連接PC、PE。如圖9，若點E、F分別落在邊AB、AC上，則結論“PC=PE”成立（不要求證明）。把圖9中的△AEF繞著點A順時針旋轉。（1）如圖10，若點E落在邊CA的延長線上，則上述結論是否成立？若成立，請給予證明;若不成立，請說明理由。（2）如圖11，若點F落在邊AB上，則上述結論是否仍然成立？若成立，請給予證明;若不成立，請說明理由。（3）記AB/BC=k，當k為何值時，△CPE總是等邊三角形？（請直接寫出k的值，不必說明理由）

分析：（1）首先過點P作PM⊥CE于點M，由EF⊥AE，BC⊥AC，可推得EF∥MP∥CB，進一步推得=，然后根據點P是BF的中點，可得EM=MC，據此可推得PC=PE。（2）過點F作FD⊥AC于點D，再過點P作PM⊥AC于點M，連接PD，可通過證明△DAF≌△EAF和△DAP≌△EAP，即可推得AD=AE和PD=PE;由FD⊥AC，BC⊥AC，PM⊥AC，可得FD∥BC∥PM，根據點P是BF的中點，推得PC=PD，再根據PD=PE，進而可推得PC=PE。（3）首先根據△CPE總是等邊三角形，可得∠CEP=60°，再推得∠CAB=60°;然后根據∠ACB=90°，求出∠CBA=30°。根據tan30°=k，可求出當△CPE為等邊三角形時k的對應值。

解答：（1）答：PC=PE成立，理由如下：如圖12，過點P作PM⊥CE于點M，因為EF⊥AE，BC⊥AC，所以EF∥MP∥CB，根據平行線分線段成比例定理易證PC=PE。（2）答：PC=PE成立，理由如下：如圖13，過點F作FD⊥AC于點D，過點P作PM⊥AC于點M，連接PD，易證△DAF≌△EAF（AAS），推得AD=AE。進而可證△DAP≌△EAP（SAS），推得PD=PE，因為FD⊥AC，BC⊥AC，PM⊥AC，所以FD∥BC∥PM，根據平行線分線段成比例定理可證得DM=MC，因為PM⊥AC，所以PC=PD。又因為PD=PE，所以PC=PE。（3）答：如圖14 ，因為△CPE總是等邊三角形，所以∠CEP=60°，所以∠CAB=60°，因為∠ACB=90°，所以∠CBA= 90°-∠CAB=90°-60°=30°，所以k==tan30°=。

本題借助從特殊到一般的遞進式的探究活動，體現了基礎與深究并重，并采取分散的形式對基本圖形中的兩個基本結論進行考查，降低了難度，加深了學生對“反A型”旋轉相似直角三角形圖形模型的理解。

2.離析提煉應用基本圖形模型解題

當復雜的幾何圖形中隱含著“反A型”旋轉相似直角三角形模型時，要從復雜的圖形中離析出基本的圖形模型，進而運用基本的圖形模型所蘊含的基本結論的證明方法有效地解決問題，這也是學生解決幾何綜合題必備的能力之一。

例題：如圖15，矩形ABCD中，AD=AB，E為矩形對角線BD上一點，過E點作EF⊥BD交CD于F，連接BF，G為BF中點，連接CG、EG。（1）試判斷線段CG和EG之間的數量關系，試求∠CGE的度數。（2）將圖15中△DEF繞D點順時針旋轉，使DF落在對角線BD上，如圖16所示，取BF中點G，連接CG、EG、EC。猜想：△CEG是否是等邊三角形？若是，請證明;若不是，說明理由。（3）將圖15中△DEF繞D點旋轉任意角度α，如圖16所示，再連接相應的線段，問（2）中的結論是否仍然成立？若成立，請給出證明;若不成立，請說明理由。

提問：你能運用上面你自己發現的模型的相應的基本證法來解決這道題嗎？思考：（1）你能從圖15、圖16和圖17中找出“反A型”旋轉相似直角三角形模型嗎？若能，是Rt△和Rt△組成了“反A型”旋轉相似直角三角形模型。

這道題是綜合2015年重慶中考數學試卷第25題和2009年山東省萊蕪市中考數學試卷的第24題進行變式得到的試題。如果去掉圖15中線段AB和AD（如圖18），就成了反“A”型旋轉相似直角三角形模型中的特殊情景;去掉圖16中線段AB和AD（如

圖19），就成了反“A”型旋轉相似直角三角形模型中將Rt△DEF繞點D順時針旋轉60°后的圖形模型;去掉圖17中線段AB和AD（如圖20），并連接BD，就成了反“A”型旋轉相似直角三角形模型中將Rt△DEF繞點D順時針旋轉任意的角度a后的一般情景。這樣通過對復雜圖形的分析，從中提煉出反“A”型旋轉相似直角三角形的基本圖形模型，復雜的問題就變得簡單化了。

解答：（1）CG=EG;∠EGC=60°。（解題過程略）（2）答：△CEG是等邊三角形。證明：如圖21 ，延長CG至點H，使得GH=CG，連接FH、EH，易證△FGH≌△BGC，可得HF=BC，∠HFG= ∠CBG，所以HF∥BC ，所以∠HFG=∠DBC=30°。易知∠EFD=∠DBC=30°，∠EDF=∠BDC=60°，進而可證∠EFH=∠EDC=120°。因為==tan∠CDB= tan60°=，=tan∠EDF=tan60°=，即=，所以△HEF≌△CED，所以==，∠HEF=∠CED 。易證tan∠ECG==，所以∠ECG=60°。所以△CEG是等邊三角形。（3）答：（2）的結論仍然成立。證明：如圖22，延長CG至點H，使得GH=CG，連接FH、EH、BD。延長CD，交EF于點N，交HF的延長線于點M。易證△FGH≌△BGC，所以HF=BC，∠HFG=∠CBG，所以HF∥BC，所以∠HMN+∠BCD= 180°。因為∠BCD=90°，所以∠HMN=90°。 進而可證得∠HFE=∠CDE。 因為==tan∠CDB=tan60°=，=tan∠EDF=tan60°=，即=，所以△HEF∽△CED。 所以==，∠HEF=∠CED ，易證=tan∠ECG=，所以∠ECG=60°，所以△CEG是等邊三角形。故（2）中的結論仍然成立。

設計意圖：教師通過兩個例題的鞏固訓練，引導學生學會借助基本圖形模型以及模型相應的基本證法來解決此問題，進一步鞏固反“A”型旋轉相似直角三角形這一基本模型，提高學生運用基本模型解決綜合題的能力，使復雜問題簡單化，陌生問題熟悉化。教師還通過比較，讓學生深刻體驗到同一種方法在不同位置的證明難易度不同和同一種方法在相同位置的證明難易度不同，從而體驗到一題多解的妙處。

總之，從近幾年的許多中考試題看，反“A”型旋轉相似直角三角形的圖形模型有著相對比較廣泛的應用。反“A”型旋轉相似直角三角形模型的兩個基本結論在解決相關的壓軸題時起著至關重要的作用，證明反“A”型旋轉相似直角三角形模型的兩個基本結論的三種方法對解決同類問題具有一定的導向作用，所以在教學時要引導學生重視三種方法的解題功能。師生共同探究反“A”型旋轉相似直角三角形的圖形模型和兩個性質，讓學生熟識反“A”型旋轉相似直角三角形的圖形模型，掌握反“A”型旋轉相似直角三角形模型的兩個基本結論證明的三種方法，可以使學生利用反“A”型旋轉相似直角三角形的圖形模型解決與該模型有關的試題，從而培養學生應用圖形模型有效地分析問題和高效地解決問題的能力。

參考文獻：

[1]羅慶友.方法引領拓展遷移[J].中學數學教學參考，2012（11）.

[2]張良江.欲擒故縱巧應變化 靜為動逸待勞[J].中國數學教育，2013（11）.

[3]秦秀華.初中幾何教學中存在的問題及解決對策[J].成才之路，2015（06）.

[4]何雄瑛.利用基本幾何圖形解題的教學探討[J].福建中學數學，2018（01）.

[5]張麗.基于圖形分析的初中幾何變式教學的應用探究[D].南京師范大學，2015.

Research on Familiar with the Basic Geometric Model to Realize the Simplification of Mathematical Problem Solving

Hu Qingshan

（Zhongshan Middle School， Putian County， Fujian Province， Putian 351100， China）

Abstract： "Anti-A type" rotation similar right triangle model often appears in the middle school examination questions in recent years， and after the variation deduction of the experts in the middle school examination questions， there is a new situation of constant examination. In order to better solve the geometric problems of this model， teachers should guide students to observe and analyze the graphics， learn to separate this basic geometric model from the complex graphics， understand the basic conclusions contained in this basic geometric model， master this basic solution， and improve the ability of solving problems.

Key words： mathematics teaching; problem solving; geometric model; flexible application