用幾何直觀提高學生的學習能力

何曉玲

摘? 要 小學生的思維以具體形象思維為主，運用幾何直觀可幫助學生有效地將形象思維過渡到抽象邏輯思維，可以讓學生調動各種感官，充分體驗知識的形成過程，獲得生動的表象，建立數學模型，并能熟練運用數學模型解決生活中的問題。

關鍵詞 幾何直觀;課程標準;數學模型;學習能力;核心素養(yǎng)

中圖分類號：G623.5? ? 文獻標識碼：B

文章編號：1671-489X（2020）01-0065-03

1 錯題分析

五年級下冊期末考試中有這樣一道題目：

一個長方體，如果增高4 cm，就成為一個正方體，這時表面積比原來增加了96 cm2。原來的長方體的表面積是多少平方厘米？

這道題全班有14人做錯，是整張試卷錯誤率最高的題目，錯誤率達到28.6%，錯誤類型有下面幾種情況。

1）思路不清晰。一個學生的解答過程如下：

①96÷6=16（cm2）;

②16×16×6=1536（cm2）;

③（16×16+4×16+4×16）×2=768（cm2）;

④1536-768=768（cm2）。

在這個學生的解答中，可發(fā)現他的第一步算式是沒有算理的。他把96當作一個正方體的表面積，除以6得出16，看作一個面的面積;但后面又將16當成正方體的棱長，也就是長方體的長與寬;第三步又把“增高4 cm”這個數據當作長方體的高。因此，整個思路非常混亂。

2）表面積公式不熟，數據用錯。

錯題一：

①96÷4=24（cm2）;

②24÷4=6（cm）;

③6-4=2（cm）;

④（6×6+6×6+6×2）×2=168（cm2）。

錯題二：

①96÷4=24（cm2）;

②24÷4=6（cm）;

③6-4=2（cm）;

④（6×2+6×2+2×2）×2=56（cm2）。

在第一個學生的解答中，第一、二步的解答思路沒問題，求出的“6”既是正方體的棱長，又是原來長方體的長和寬;第三步求出的“2”是原來長方體的高;但在第四步運用表面積計算公式時，沒有想清楚原來長方體的長、寬、高分別是多少，正確的解答應是（6×6+6×2+6×2）×2=120（cm2）。第二個學生的解答也存在類似的錯誤。

3）沒有解答完整。有一個學生的解答如下：

①96÷4=24（cm2）;

②24÷4=6（cm）;

③6-4=2（cm）。

從這個學生的解答中可以看出，他知道一些解答步驟，但求出這些結果后，不知這些結果能做什么，屬于思路不清晰、解答不完整。

對以上分析進行反思：到底要教給學生怎樣的學習能力？怎樣提升學生的核心素養(yǎng)？筆者認為運用幾何直觀能很好地幫助教師解決這個困惑。

《義務教育數學課程標準（2011年版）》指出：“幾何直觀主要是指利用圖形描述和分析問題。借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。幾何直觀是學生空間觀念形成的基礎。小學生的思維以具體形象思維為主，幾何直觀能力是思考數學問題、發(fā)展數形結合思想的基礎，是學生必備的一種基本數學素養(yǎng)。教師在教學中應充分運用幾何直觀使知識形成生動表象，形成概念，促進學生有效思維，提高學習能力，培養(yǎng)學生的數學學科核心素養(yǎng)。

2 借助實物操作，直觀感受表面積變化規(guī)律

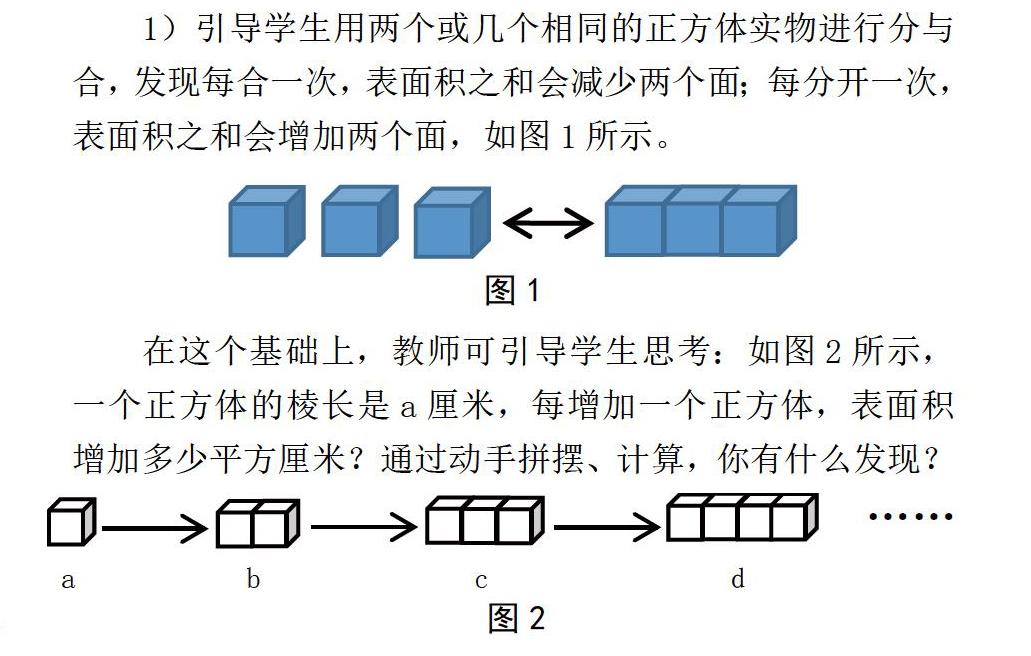
1）引導學生用兩個或幾個相同的正方體實物進行分與合，發(fā)現每合一次，表面積之和會減少兩個面;每分開一次，表面積之和會增加兩個面，如圖1所示。

在這個基礎上，教師可引導學生思考：如圖2所示，一個正方體的棱長是a厘米，每增加一個正方體，表面積增加多少平方厘米？通過動手拼擺、計算，你有什么發(fā)現？

學生獨立思考，動手操作，小組合作探究，交流討論，展示不同的思路。

【生1】從圖2a到圖2b，表面積之和減少兩個面，所以可以用6a2×2-2a2=10a2

【生2】可以先找出每幅圖長方體的長、寬分別是多少。從這四幅圖中可以看出，圖2b的長是2a厘米，圖2c的長是3a厘米，圖2d的長是4a厘米;寬和高不變，都是a厘米。運用長方體的表面積公式計算，圖2b的表面積是（2a×a+2a×a+a2）×2=10a2，同樣計算方法可以算出圖2c、圖2d的表面積分別是14a2平方厘米，18a2平方厘米，每個圖形都比前一個圖形多了4a2平方厘米。

【生3】從圖中可以看出，每個圖形露出的正方形的個數是有規(guī)律的，不變的是左右兩個面，變的是每次多了前、后、上、下四個小正方形，只要算出每個長方體是由幾個這樣的小正方形圍成的，再乘每個正方形的面積，就可以算出表面積了。圖2c有3×4+2=14個小正方形，長方體的表面積就是14a2平方厘米;如果是圖2f，就有6×4+2=26個小正方形，長方體的表面積就是26a2平方厘米。

教師再拋出問題：如果是n個小正方體拼成的長方體，它的表面積是多少平方厘米呢？有了前面的基礎，學生就能很快地推理出n個長方體表面積為（4n+2）a2平方厘米。

長方體或正方體的拼擺過程真正讓學生動手去操作，通過摸、擺、拼、剪等具體行動，讓學生感知表面積中的變與不變，通過操作、觀察、分析等活動發(fā)現規(guī)律。這樣才能實現學生主體真正的發(fā)展，教學才能真正有效落實。

2）將兩個相同的長方體不同方向拼擺，找分與合表面積的變化。

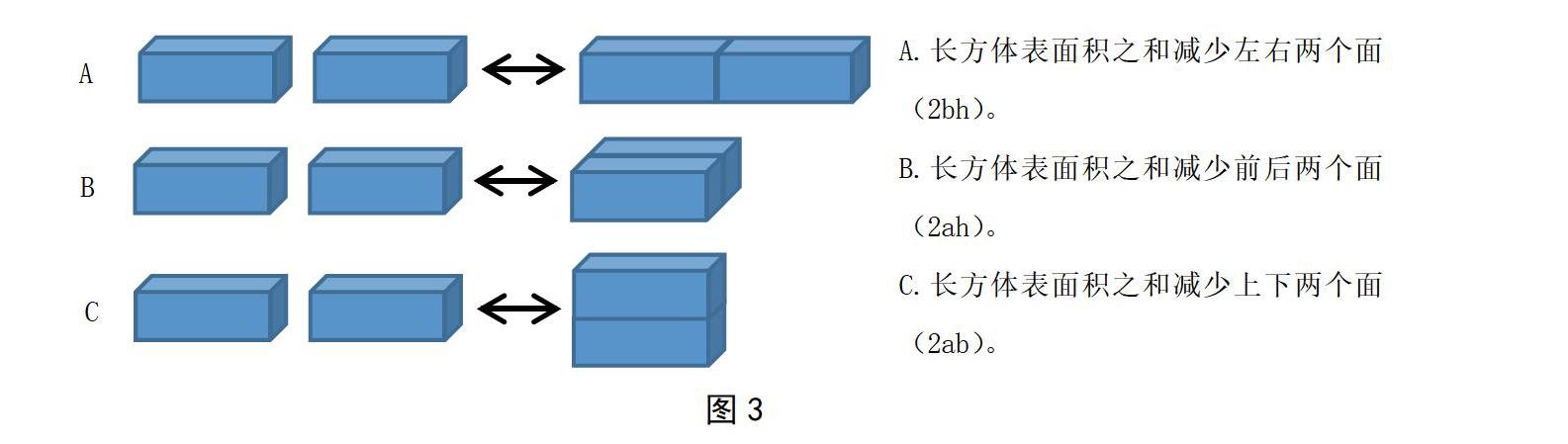
拼一拼、說一說：如圖3所示，將兩個完全相同的長方體合在一起，表面積之和會發(fā)生什么變化？你發(fā)現了什么？

學生動手操作，獨立思考，小組合作探究，交流討論，發(fā)現有三種不同的拼擺方法，表面積減少是不同的：將最大的面合在一起，表面積減少的最多;將最小的面合在一起，表面積減少的最少。反過來，如果將一個長方體截成兩個長方體，表面積增加最多的就是平行于最大的面切開，表面積增加最少的就是平行于最小的面切開。

3 用幾何直觀促知識的理解與內化

在教學五年級下冊“長方體和正方體”這個單元的知識時，學生第一次接觸立體圖形，對空間的想象有很大的難度。因此，多讓學生動手摸一摸、擺一擺、涂一涂、折一折，豐富學生的表象，多角度地觀察與思考，找到解決問題的方法。在這個單元中，學生最不易掌握的就是長方體的表面積計算，因為根據生活實際情況，有求表面積有六個面，也有求五個面（無蓋、粉刷教室等），還有可能求四個面（煙囪、餅干盒貼商標等）。在求長方體四個面（前后左右）的面積時，很多學生會用“長×高×2+寬×高×2”，或者用“（長×高+寬×高）×2”這兩種方法。教師這時可讓學生拿一個沒有上、下底的紙盒沿高展開，發(fā)現展開圖是一個大的長方形，這個長方形的面積就是前后、左右四個面的面積之和，如圖4所示。

這個長方形的長就是長方體底面周長，寬就是長方體的高，所以這四個面的面積之和還可以通過“底面周長×高”計算出來，也說是用“（長+寬）×2×高”來計算四周的面積，在此基礎上加上面的面積和下面的面積，就可以求出表面積。這樣就將求長方體的表面積轉化成求一個平面圖形的面積。通過讓學生動手剪一剪、擺一擺、比一比，學生掌握了多種求表面積的方法，并能結合直觀圖有理有據地說出自己的想法。

4 學會用畫圖方法幫助理清解題思路

除了動手操作充分感知，教師應引導學生學會用圖來分析題意、理解題意、理清解題思路，能主動用圖說事、用圖分析、用圖說理。學生的作圖能力不是與生俱來的，他們需要教師正確的引導與示范，并進行學習與練習。教師可在學生大量觀察各種各樣的長方體、正方體實物或模型的基礎上，提出問題：在觀察長方體、正方體時，最多能看到幾個面？

如圖5所示，教師示范畫出能看出三個面的長方體、正方體，先畫正面（長方形或正方形），再畫另兩個面（平行四邊形），并在合適的位置標上數據。讓學生學著畫，教師要鼓勵學生，對畫得好的學生及時表揚，展示其作品;對畫得不夠好的學生，應指出不足在哪里，并引導他重新畫，直到畫好為止。

學生在根據題意會畫圖的基礎上，還要看懂圖意，會分析、理解圖意。如這道題：

一個長方體，如果增高4 cm，就成為一個正方體，這時表面積比原來增加了96 cm2。原來的長方體的表面積是多少平方厘米？

根據題目的描述“一個長方體，如果增高4 cm，就成為一個正方體”，作圖時就可先畫出一個正方體，然后標出增高的4 cm，這樣就把正方體分割成兩個長方體，如圖6所示。從圖6中可以看出，每個長方體都有兩個相對的面是正方形，長和寬是相等的，前、后、左、右四個面的面積是相等的。

增高4 cm，表面積增加96 cm2，增加的面積在哪兒呢？這是本道題解題的關鍵。因此，畫出圖后會正確地看圖，是每位學生必須掌握的本領。教師在引導學生觀察圖形之后，思考問題：增高之后，表面積增加在哪兒呢？學生經過思考、討論、交流發(fā)現，表面積并沒有增加六個面，因為兩個長方體拼在一起后，中間兩個面合在一起隱藏了，不能算表面積的一部分，這樣下面這個長方體只剩前、后、左、右、下等五個面。如果要使下面一個長方體的表面積不變，就要將上面一個長方體的上面割補移到下面長方體的上面（抵消法），真正多出來的表面積只有上面長方體的前、后、左、右等四個面，如圖7所示。

如圖8所示，這道的解題思路是：

①先求每個面的面積（或展開圖的底面周長）：96÷4=

24（cm2）;

②再求長方體的長或寬：24÷4=6（cm）;

③再求原來長方體的高：6-4=2（cm）;

④最后求原來長方體的表面積：

s=（ab+ah+bh）×2

=（6×6+6×2+6×2）×2

=120（cm2）

用幾何直觀畫圖理解有關“增高”引起表面積增加的問題，也可以解決“降高”引起表面積減少的問題。通過對比發(fā)現，不管是“增高”還是“降高”，表面積始終變的只有四個面的面積，都可以先找展開圖的底面周長或者每個面的面積，這就是這道題的解題關鍵。這樣就建立起數學模型，以后遇到類似的題目，都可以用這個數學模型去解決。

教師通過安排合理的操作環(huán)節(jié)，給學生提供更多親自動手實踐的機會，同時給學生提供了更大的思維空間。在動手操作過程中，學生就會把操作與思維聯系起來。動手操作可以使學生對知識產生新的理解和看法，進一步理解和鞏固知識，還能夠在新的發(fā)現、新的感悟中碰撞出創(chuàng)新意識的火花。

5 結語

總之，幾何直觀能利用圖形描述和分析問題，借助幾何直觀，讓學生用摸、擺、拼、剪等動手操作形成生動、豐富的表象，把復雜的數學問題變得簡明、形象。幾何直觀可以幫助學生理解抽象的數學知識，感知知識的形成過程;可以幫助學生建立數學模型，進而運用數學模型解決生活中的問題。“授之以魚，不如授之以漁。”教師不但要善于使用幾何直觀進行教學，還應指導學生主動運用幾何直觀學習，用畫圖的方法分析題意、理解題意、理清解題思路，從而提高學生的學習能力，培養(yǎng)學生的核心素養(yǎng)。

參考文獻

[1]孔凡哲，史寧中.關于幾何直觀的含義與表現形式：對《義務教育數學課程標準（2011年版）》的一點認識[J].課程·教材·教法，2012（7）：92-97.