滲透數學文化　落實核心素養

李江華

[摘 要]在數學教學中滲透數學文化，有利于培養學生的核心素養.在《平均變化率》教學中，教師以數學文化為主線，以課堂探究為方法，以問題設計為引領，有效開展數學教學活動，很好地培養了學生的核心素養.

[關鍵詞]教學文化;核心素養;平均變化率

[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2020）20-0009-04

《中國學生發展核心素養》中明確了教育改革的行動綱領和終極目標是培養全面發展的人. 《普通高中數學課程標準（2017年版）》（簡稱《課標方案（2017年版）》）要求實現“人人都能獲得良好的數學教育，不同的人在數學上得到不同的發展”，重視數學實踐和數學文化. 《課標方案（2017年版）》強調數學與生活以及其他學科的聯系，提升學生應用數學解決實際問題的能力，同時注重數學文化的滲透;不斷引導學生感悟數學的應用價值和文化價值，多次提出要將數學文化融入課程內容.? 要通過數學文化的滲透，讓學生樹立正確的人生觀、價值觀和世界觀，以達到“立德樹人”的效果.? 教育部考試中心也提出了滲透數學文化的數學命題要求，要求通過多種渠道滲透數學文化，如有的試題將通過數學史展示數學文化的民族性與世界性. 《課程方案（2017年版）》中明確提出，數學文化是指數學的思想、精神、語言、方法、觀點以及它們的形成和發展，包括數學在人類生活、科學技術、社會發展中的貢獻和意義以及與數學相關的人文活動. 這就要求教師在平時的教學中要有意識地滲透數學文化，通過數學文化的滲透促進學生的發展. 基于這樣的背景，筆者在區優質課評比教學中做了一些嘗試，收到不錯的效果.

一、教學過程

1. 文化之旅

師：從今天開始，我們將學習選修2-2第一章《導數及其應用》，同學們有沒有聽說過導數？

師：看來大家對導數完全不了解，不過沒關系，我們很多熟悉的老朋友一直很關心它，為了它的發展，耗費了大量的精力.

師：請大家和我一起來一次文化的穿越之旅.我們先來看公元前200多年，古希臘的科學泰斗阿基米德用積分的觀點求出了球的體積. 他用球體“薄片”的疊加與球的外切圓柱及相關圓錐“薄片”的疊加，并用杠桿原理得到球的體積. 我們再把目光轉向公元5世紀的東方，我國南北朝時期出了祖沖之、祖暅兩位偉大的數學家，他們提出了“冪勢既同，則積不容異”的祖暅原理，這是積分概念的雛形. 微分觀念的發生比積分大概遲了2000年，公元16世紀的意大利，伽利略發現了自由落體的運動規律，提出了瞬時速度，這是導數的啟蒙. 到了17世紀，西方出了兩個天才，一個是百科全書式的全才——牛頓，一個是歷史上少見的通才——萊布尼茲. 在總結了許多數學家的經驗之后，牛頓從運動變化的觀點考慮問題，萊布尼茲從幾何學的角度考慮問題，分別獨立建立了微積分學，他們對微積分學最突出的貢獻是建立了微積分基本定理. 對于微積分學，恩格斯做出這樣的評價：只有微積分學才能使自然科學有可能用數學來不僅僅表明狀態，而且也表明過程：運動.

師：微積分學不僅在數學中占有重要的地位，還為其他學科的發展提供了強有力的工具. 那么導數究竟是什么呢？它有哪些應用呢？在接下來的一段時間內我們將逐步揭開它的神秘面紗.

設計意圖：通過微積分的發展史進行數學文化的滲透，既讓學生了解了微積分的產生過程，又學習了數學家的優秀品質.牛頓和萊布尼茲的故事教會學生要善于獨立思考.

2. 情境引入

師：這個世界充滿著變化，有些變化幾乎不被人們所察覺，而有些變化卻讓人們發出感嘆與驚呼. 同學們，最近你能感受到的最大變化是什么？

生：天氣突然變冷了.

師：很好.12月3號蘇州市最高溫是20 ℃，12月8號蘇州市的最高溫只有4 ℃，用天氣預報員的話說，就是進入了“速凍”模式. 蘇州市2004年4月18號最高氣溫是18.6 ℃，4月20號的最高氣溫是33.4 ℃，短短兩天時間，氣溫“陡增”14.8 ℃，悶熱中的人們無不感嘆“天氣熱得太快了”.但是如果我們把3月18 號的最高氣溫3.5 ℃與4月18號的最高氣溫作比較，會發現它們的溫差為15.1 ℃，甚至超過了14.8 ℃，而人們都沒有發出上述感嘆，這是為什么呢？

生：前者變化太快，后者變化太慢.

師：在生活中，你怎么表達這個變化快和慢的？

生：用平均變化值表示.

設計意圖：通過學生身邊的例子，很容易把學生引入到情境中來，激發學生的學習興趣. 用生活的語言表達變化快慢，體現數學源于生活.

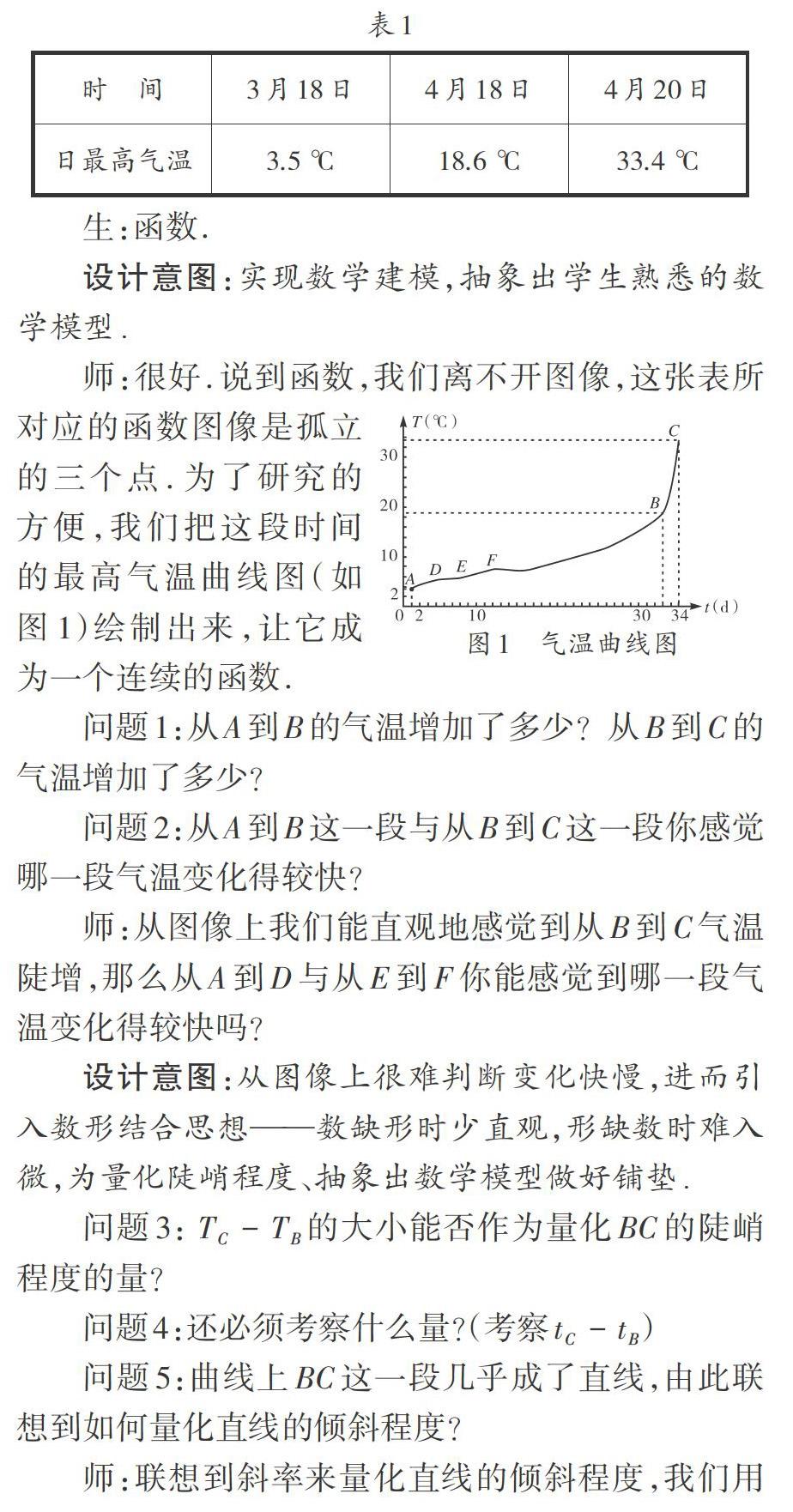
師：不難看出，雖然氣溫相差不大，但是平均變化值卻相差很大，這也說明只看溫差是不行的，還要看這個時間段的長短. 大家再看這張表（表1），如果我們把3月18號看成第一天，用1來代替，相應的后面兩個日期換成數字32，34，從數學的角度看，它是什么數學模型？

生：函數.

設計意圖：實現數學建模，抽象出學生熟悉的數學模型.

師：很好.說到函數，我們離不開圖像，這張表所對應的函數圖像是孤立的三個點.為了研究的方便，我們把這段時間的最高氣溫曲線圖（如圖1）繪制出來，讓它成為一個連續的函數.

問題1：從A到B的氣溫增加了多少？從B到C的氣溫增加了多少？

問題2：從A到B這一段與從B到C這一段你感覺哪一段氣溫變化得較快？

師：從圖像上我們能直觀地感覺到從B到C氣溫陡增，那么從A到D與從E到F你能感覺到哪一段氣溫變化得較快嗎？

設計意圖：從圖像上很難判斷變化快慢，進而引入數形結合思想——數缺形時少直觀，形缺數時難入微，為量化陡峭程度、抽象出數學模型做好鋪墊.

問題3： [TC-TB]的大小能否作為量化BC的陡峭程度的量？

問題4：還必須考察什么量？（考察[tC-tB]）

問題5：曲線上BC這一段幾乎成了直線，由此聯想到如何量化直線的傾斜程度？

師：聯想到斜率來量化直線的傾斜程度，我們用比值[TC-TBtC-tB]來近似地量化BC這一段曲線的陡峭程度，并稱這個比值為氣溫在區間[32， 34]上的平均變化率.

設計意圖：建模的過程中抓住關鍵點——區間，同時隱藏著以直代曲的數學思想，通過滲透全新的數學思想來滲透文化.

師：我們如何用數學語言刻畫平均變化率？

教師用幾何畫板動態演示過程（如圖6）：我們發現隨著點B越來越接近點A，這個線段AB與曲線AB越來越貼近，這個時候平均變化率也越來越精確地表達曲線的陡峭程度. 這個時候平均變化率越來越接近2.

設計意圖：通過動態演示，從形到數，讓學生感覺當區間逐漸變小時平均變化率越來越逼近“精確”.

5. 文化滲透

師：這里隱藏著“以直代曲”和“無限逼近”的極限思想.說到這兩種思想，不得不提及中國古典數學理論的奠基人之一——劉徽，他是公元3世紀世界上最杰出的數學家，撰寫有《九章算術注》和《海島算經》，他的“割圓術”是人類歷史上第一次將“以直代曲”和“無限逼近”的極限思想引入數學，這也是他對世界數學做出的最突出貢獻. 很可惜的是，他只做了這樣的實驗，從內接正六邊形開始，每次邊數倍增，一直到內接3072邊形，得到了實驗數據，但他沒有嚴密的邏輯推理，讓人類得到圓周率的時間推遲了200多年，所以我們在平時的學習解題中，不能光有答案，要注意嚴密的邏輯推理過程，要知其然還要知其所以然.

設計意圖：滲透數學文化——數學史，通過中國古代數學家的故事，培養學生的民族自豪感，增強學生的文化自信. 同時通過數學家的故事，讓學生在平時的學習中重視邏輯推理.

師：我們通過前面的學習以及剛才的演示，應該很容易感受到：平均變化率體現變化的結果，并沒有體現變化的過程.? 如何讓平均變化率也關注過程呢？當年伽利略在這個問題上研究了好長時間，究竟怎么體現過程呢？我們將在下節課繼續研究.

6. 課堂小結

（1）今天同學們學到哪些新知識？

（2）本節課你體會到了哪些數學思想？

（3）本節課你體會到了哪些數學應用？

（4）本節課你感受到了哪些數學史？

二、教學反思

1. 以數學文化為主線，激發學生數學思維

課堂是學生學習數學知識的主要途徑，對數學文化的學習，應更多地體現在課堂教學之中.張奠宙先生認為“數學文化必須走進課堂”.? 數學的文化內涵往往以潛移默化的形式存在，只有教師有意識地將文化觀念滲透于數學課堂教學之中，才能讓學生感悟這種“看不見的文化”.? 在課堂中合理地融入數學文化，不僅可以增加數學課堂的趣味性，更能引發學生的主動思考，激發其數學思維，這樣才能將外在的數學活動轉化為內在的思維活動.? 這就要求教師在課堂中有意識地加入數學文化元素，讓學生清楚知識的來龍去脈，能更主動地參與知識的發生發展過程.? 在歷史的發展中理解數學知識，這樣的學習才是有基礎、有源頭的，才可以在循序漸進中激發學生的數學思維.? 本節課的教學設計，以數學文化為開端和結尾，形成一條主線將知識串成了有序的知識鏈，引導學生一步步在數學史中穿越而來，感受到了數學的魅力，激發了數學思維.

2. 以課堂探究為方法，培養學生核心素養

數學核心素養如何形成？不是依賴記憶與模仿，而是在探究實踐中形成的思維與方法，這是一個日積月累、不斷積累的過程.? 因此在教學設計中，教師要注重學生的探究實踐，精心預設問題，啟發學生既要關注探究過程，重視探究的過程，要給學生留時間思考，更要借助工具讓學生容易理解.? 這節課教師借助圖像，借助幾何畫板，借助生活實例，使數學教學從以知識為本走向以素養為本. 在探究實踐中，學生不僅獲得了知識與技能，更重要的是積累了數學活動經驗，培養了數學核心素養.

3.? 以問題設計為引領，促進學生深層思考

在教學活動中，隨著問題的展開、推進，適時地對學生進行啟發與點撥，對問題進行層層分解、層層遞進，不僅有利于學生解決問題，更能及時捕捉學生的思維亮點，促進學生進行深入鉆研.? “凡事預則立，不預則廢.”好的策劃才能出好戲，教學中更是如此.? ?在課堂教學中很多“亮點”都是預設的.? 當然“亮點”的創設來源于獨到的教學見解，新穎的活動體驗，生動的教學方法.? 本節課，教師按照學生的思維發展層次，以遞進式的問題和連續不斷的追問，分階段讓學生獲得知識、技能和經驗，逐步將學生引入更深層的思考.? 一個個問題的提出、探究、解決，使教學過程不再是簡單的知識傳授，而更多的是培養學生的問題意識和思維能力.

[? ?參? ?考? ?文? ?獻? ?]

[1]? 中華人民共和國教育部.普通高中數學課程標準（2017年版）[S].北京：人民教育出版社，2018.

[2]? 史寧中，王尚志.普通高中數學課程標準（2017年版）解讀[M].北京：高等教育出版社，2018.

（責任編輯 黃桂堅）