例談小學生“數感”的培養途徑

【摘要】本文結合例題論述培養小學生數感的途徑，認為教師應在數的認識之初、在運算過程中、在解決問題的過程中以及在實踐中培養小學生的數感，將數感培養滲透在數學教學中。

【關鍵詞】數感 小學數學 培養

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2020）25-0122-03

《義務教育數學課程標準》（2011年版）認為：“數感主要表現在理解數的意義，并能用多種方法來表示數;能在具體的情境中把握數的相對大小;能用數來表達和交流信息;能為解決問題而選擇適當的算法;能估計運算結果，并對結果的合理性做出解釋。”簡單地說，“數感”指關于數與數量、數量關系、運算結果估計等方面的感悟。“數感”是《義務教育數學課程標準》（2011年版）中給出的義務教育階段數學內容所涉及的十個核心概念中的第一個，它的重要性不言而喻。因此，教師要重視學生“數感”的培養，促使學生在數學的學習過程中建立數感、發展數感。

一、在數的認識之初培養“數感”

培養學生的“數感”不是一朝一夕的事情，它需要經歷一個比較漫長的過程，學生在這過程中不斷學習、不斷積累對數的認知和體驗。因此，教師首先要認識到“數的認識”是小學課程的重要內容。其次，教師在學生對數的認識之初就要對學生進行數感培養，讓學生對數產生興趣，提升學生對數的敏感度，讓學生從最初的認識數過渡到理解數的意義。

例如，小學一年級學生通過“數一數”的方法對“數”的概念建立初步的認識。

例題1：請小朋友數一數框內物品的數量，再連上相應的數字。（如圖1）

例題2：請小朋友認真數一數，再畫出相對應的圓圈數。（如圖2）

又如，在小學一年級上冊就有“數的大小比較”的內容，學生通過“比一比”的方法來感受和理解數。

例題3：請把同樣多的物體圖和點子圖用線連下來。（如圖3）

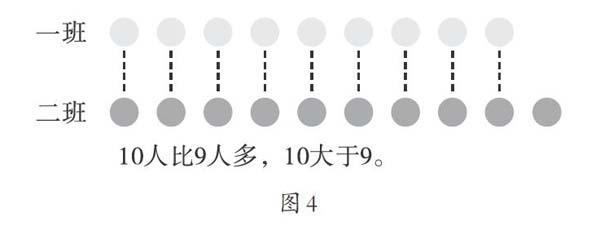
例題4：比一比哪個班的人數多，哪個班的人數少。（如圖4）

學生觀察這些與生活密切相關的圖片，思考、感悟數的概念，形成對數的初步認識：5個圈對應的是5個黑點，5=5，7朵花對應7個黑點，7=7，10個人比9個人多，理解了10>9這個抽象的數量關系。學生腦海中的對數的初步認識將會為以后學習整數、小數、分數、負數等數的知識打下基礎。

二、在運算過程中培養“數感”

（一）算法多樣

數的運算是小學數學的重要內容，它貫穿小學數學教學的全過程。教師在教學數的運算時，不僅要教會學生運用數進行表達和交流，還要培養學生良好的數感，讓學生在學會運用數學思維感悟數理、算理的同時，理解數是如何參與運算的。

例如，在小學一年級“9加幾”的教學過程中，教師可以引導學生利用已有的生活經驗，初步理解“湊十法”，掌握9加幾的進位思維過程，并能正確計算9加幾。

例題5：如圖5所示，有9根紅色小木棒和4根藍色小木棒，一共多少根小棒？

學生可以運用“數一數”的方法，直接數出小木棒的數量;還可以運用“湊十法”進行運算。根據“湊十法”，學生把其中10根小木棒圈起來，湊成10，再用10加上圈外的3根小棒就可以得出運算結果（如圖6、圖7）

學生通過親自動手畫圈，在感受“9加幾”“8加幾”“7加幾”等運算算理的同時，對數的組成有深刻的認識，不僅提高了運算能力，還發展了數感。

又如在教學“20以內的進位加法”時，有這樣一道題目。

例題6：籠子里有5只白兔和3只灰兔，籠子外有5只白兔和2只灰兔，一共有多少只兔子？

有些學生運用“數一數”的方法，直接數出兔子的總數量;有些學生把籠子里的兔子數量加上籠子外面的兔子數量，列式為：8+7=15（只）;有些學生認為應列式為：10+5=15（只），理由是白兔有10只，灰兔有5只，所以一共有15只兔子。

教師的引導和學生的自主探索，讓學生認識到解決問題的方法是多樣的。這樣不僅激發了學生對數的興趣，加深了學生對數的理解，也為學生之后的學習打下良好的理論與實踐基礎。

（二）掌握運算規律

學生在學習“數的運算”的過程中掌握數與數之間的運算規律，不僅可以提升數學思維，還可以提升數感。

例如在教學“加法交換律和加法結合律”時，有這樣一道例題（如圖8）。

生1回答：跳繩的人數=28+17=45（人），參加活動總人數=28+17+23=（28+17）+23=68（人）

生2回答：跳繩的人數=17+28=45（人），參加活動總人數=28+17+23=28+（17+23）=68（人）

……

學生通過自主探索發現，兩個數相加，交換加數的位置，和不變，即a+b=b+a;三個數相加，先把前兩個數相加，再加第三個數，或先把后兩個數相加，再與第一個數相加，和不變，即（a+b）+c=a+（b+c）。通過觀察，學生還可以感受到運用加法結合律可以讓運算更靈活、更快捷，如例題中的運算，先把17和23相加可以得整數40，40+28，通過口算就能快速得出答案68。學生通過學習運算規律，理解了數與數之間的關系，提高對數的敏感度。

又如，“商不變規律”是一個比較抽象的數學規律，它的文字描述是：在除法里，被除數和除數同時乘或除以一個相同的數（0除外），商不變。教師可以設計生動的教學情境，讓學生身臨其境地感受數量變化，在理解這一數學規律的同時，提升學生的數感。

例如，教師在黑板上寫一串式子：6÷3=? ，12÷6=? ，18÷9=? ，24÷12=? ……接著，教師拿出6支筆，平均分給3名學生，每人分得2支筆;再拿出12支筆，平均分給6名學生，每人分得2支筆;又拿出24支筆，平均分給12名學生，每人分得2支筆……學生思考：為什么筆的總數增加了，每個人分得的筆的數量沒有增加呢？雖然筆的總數增加了，但是學生的人數也增加了;筆的數量增加的倍數與學生數量增加的倍數相同，所以學生每次分得的筆的數量沒有變化。（如圖9）

學生通過親身體驗，理解了數的變化、數與數之間的變化關系中隱藏的數學運算規律，并在理解之后用自己的語言表述數學運算規律，更有利于發展“數感”。

三、在解決問題的過程中培養“數感”

運用數學知識解決問題是小學數學課程的重要內容之一。解決問題在考查學生對數學基礎知識的掌握的同時，也考查學生對數量關系的理解及運算能力。因此，學生在解決問題過程中，不僅要感知數的意義，還要運用數學思維觀察、分析事物，發現客觀世界的規律，學會用數學方法解決生活實際問題。教師要有意識地幫助學生建立數學模型，培養、發展學生的“數感”。

“雞兔同籠”問題是我國古代的數學名題之一，是小學數學的拓展內容。“雞兔同籠”問題其實是一類問題的總述，其背后隱藏著類似的解題思維和解決策略。教師在教學過程中，可以從原題中變換出其他題目，有利于學生探究問題的規律，也有利于提升學生的“數感”。

如圖10所示：“雞兔同籠，有9個頭，26條腿。雞、兔各有幾只？”教師可引導學生通過動態猜想來解決問題：假設有1只雞，那就該有8只兔，腿的數量是34條，不符合題意;假如有2只雞，那就該有7只兔，腿的數量是32條，也不符合題意……假如有5只雞，那就該有4只兔，腿的數量是26條，剛好符合題意，所以正確答案是雞有5只，兔有4只。學生通過這樣動態的猜想，發展了“數感”。

四、在實踐中培養“數感”

《義務教育數學課程標準》（2011年版）強調：“教師要利用實際生活與數學息息相關的案例，為學生創設學習情境，促進數學知識與實際生活的聯系，提高學生解決問題的能力。”數學源于生活，與日常生活密切相關，是生活經驗的高度總結，最終也將服務于生活。因此，教師要讓學生在生活中經歷數學學習、體驗數學學習，在生活中積累與數學相關的基本經驗，發展數感。

例如，“估算”在日常生活與數學學習中有著十分廣泛的應用，增強學生估算能力、估算意識能讓學生數感增強。

教師出示例題：某學校五年級六個班的人數如下表，請估算出五年級學生總人數。

[班級 一班 二班 三班 四班 五班 六班 人數 43 47 45 48 46 42 ]

生1：如果把這六個數看成50，約有50×6=300（人）;

生2：如果把這六個數看成40，約有40×6=240（人）;

生3：我認為他們的估算比較粗糙，我認為應該用四舍五入的方法把47、45、48、46看成50，把43、42看成40，那么五年級約有50×4+40×2=280（人）

生4：我觀察發現這六個數都比較接近45，可以估算為45×6=270（人）

……

教師對學生的大膽估算加以肯定。這道題目的準確答案是271人，教師可以引導學生把自己估算的結果與準確答案相比較，看看差距是多少，為什么會出現這樣的差距，從而讓學生反思自己的估算方法。

生1反思：我把每個數看成50，數估大了，要調小。

生2反思：我把每個數看成40，數估小了，要調大。

生3反思：運用四舍五入的方法估算比較好一些。

生4反思：取中間數的方法比較準確。

......

學生通過試估算，然后進行多種方法的對比、反思，最后找出最有效的估算方法，得出比較接近準確值的估算值。在解決這個生活問題的過程中，不僅提高了學生的思維能力，還提高了學生對數的敏感度，提升了“數感”。

學生“數感”的培養是一個漫長的、漸進的過程，學生要充分地體驗、充分地感知。教師要把對學生“數感”的培養滲透在教學的各個方面，如在數的認識之初、在數的運算過程中、在解決問題的過程中、在實踐體驗過程中，等等，這樣才能提升學生的數感，提高學生解決問題的能力，提升學生的數學學科核心素養。

作者簡介：麥彩榮（1969— ），廣西東興人，一級教師，研究方向為小學教學。

（責編 劉小瑗）