淺談二次函數中動點探究

梁和

◆摘 ?要：動點問題一直是初中階段的熱點問題，近幾年來的中考過程中，對學生的動點問題考察層出不窮。在中學階段二次函數的動點問題一直被學生成為“頑固分子”這就需要配教師在教學的過程中，結合實際的例題來為學生進行分析，從而總結出二次函數動點問題的解題思路，幫助學生更好的解決二次函數動點問題。

◆關鍵詞：二次函數;動點問題;數學教學

在初中的數學過程中，將數學知識分為了來能夠大部分，分別為幾何與函數。但是二次函數動點問題的出現，將這兩方面的數學知識進行了整合，使得學生在進行二次函數的動點問題解決時，能夠融入相應的幾何知識。因此這種綜合式的考察方法，能夠幫助學生更好的將數學作為一整個完整的體系來進行學習。以下是幾種常見的二次函數動點問題。

一、二次函數動點構建直角三角形

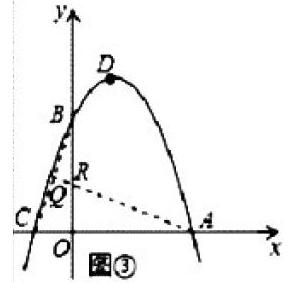
一直二次函數y=ax2+bx+3的圖象分別與x軸交于點A（3，0），C（-1，0）與y軸交于點B，點D為二次函數圖象的頂點，首先求出二次函數的關系式，其次求出在X軸上取動點P（m，0）且1

本題一共分為了三個部分，第一部分是求出二次函數的關系式，在解題的過程中，只需要將A點的坐標以及C點的坐標帶入原題當中已經給出的函數方程式這樣就能夠得出二次函數的關系式為y=-x2+2x+3。

在第二部分的解題過程中，我們已知動點的取值范圍以及在第一部分解出的方程式，并且知道點。因此我們可以通過帶入，找到點D的具體坐標：y=-x2+2x+3=-（x-1）2+4這樣得出點D的坐標為（1，4）。然后設線段A表所在的直線的函數關系式為y=kx+c然后分別將A點的坐標（3，0）以及C點的坐標（-1，0）進行帶入，得出函數關系式：y=-x+3同理可知線段AD所在的直線關系是為y=-2x+6。原題中給出了點p的坐標為（m，0）點E的坐標就是（m，-m+3）點F的坐標就是（m，-2m+6）因此得出EP之間的距離為-m+3，EF之間的距離為-m+3從而得知EF=EP。

在第三部分的解答過程中，就可以通過構建直角三角形來解決。

我們可以鏈接BC，過點R做RQ⊥BC，垂足為Q。這樣在二次函數當中就出現了兩個直角三角形，一個是RT△CQA，一個是RT△BCO。我們知道C的坐標為（-1，0）這樣就能夠得到OC=1，OB=3根據勾股定理可以得知，BC為的距離，并且通過兩個直角三角形得知△BQR與△AOB為相似三角形，進一步求得RQ與BR之間的關系，從而得知當A，R，Q三點共線時，值最小、這樣救恩能夠通過相似三角形的定理來解出最小值。

二、二次函數動點構建特殊四邊形

在二次函數的動點問題解決過程中，學生還會遇到與四邊形相關的內容，這時學生就需要根據自己的所學內容，來構建一個特殊的四邊形。

如圖，已知拋物線C1與坐標軸的交點是A（-4，0）B（-2，0）E（0，8）求拋物線C1關于原點對稱的拋物線C2的解析式;設拋物線C1的頂點為M，拋物線C2與x軸分別交于C、D兩點，頂點為N，四邊形MDVA的面積為S.若點A，點D同時以每秒1個單位的速度沿水平方向分別向右、向左運動，與此同時，點M，點N同時以每秒2個單位的速度沿堅直方向分別向下、向上運動，直到點A與點D重合為止。求出四邊形MDN4的面積S與運動時間1之間的關系式，并寫出自變量1的取值范圍;當1為何值時，四邊形MDN4的面積S有最大值。

在這一題當中總共分為了四個部分。在第一部分解答過程中，可以先確定點A，B，E關于原點的對稱點點D，C，F通過這六個點，帶入拋物線C2的解析式從而得出拋物線的解析式：y=-x2+6x-8。

在第二部分的解題過程中，由（1）的結果可以算出點M和N的坐標：M（-3，-1）N（3，1）然后添加輔助線過點N作NH⊥AD，垂足為H當運動到時刻t使，AD=2OD=8-2t，NH=1+2t。根據中心對稱的性質，可知MDNA組成了一個平行四邊形。這樣就能夠通過平行四邊形的面積來計算出點t的取值范圍。

在第三部分的解答過程中直接將t的取值范圍帶入到計算公式當中即可。在第四部分的解答過程中，主要考察動點以及舉行的定義。因此可以通過AD=AM來證明四邊形MDNA為矩形，從而解出t的值。

三、二次函數動點構建等角三角形

如圖，已知拋物線y=-=x2+hx+c與坐標軸交于ABC三點，點A的橫坐標為-1，過點C（0.3）的直線y=-3/4tx+3與x軸交于點Q，點P是線段BC上的一個動點PH⊥OB于點H.若PB=5t，且0<1<1.確定b，c的值;寫出點B.Q.P的坐標（其中Q.P用含t的式子表示）;依點P的變化，是否存在t的值，使△PQB為等腰三角形？

這一題考查了函數、相似性代數、幾何知識等問題，尤其是在第三部分，主要是對于等腰三角形的分類討論。這一類的二次函數動點問題相對解法較多，學生在解決問題的過程中可以嘗試著用多種方式進行解答。

第一部分通過帶入可知b=9/4，c=3，第二部分為B（4，0）Q（4t，0）P（4-4t，3t）第三部分t的值會有三種不同的情況：

第一種情況是PQ=PB，這時PH與OB垂直，GH=HB所以t的值為1/3

第二種是PB=QB這時t的值為4/9

第三種使PQ=BQ，在這種情況下，我們可以用三種方式進行解答：

第一種，可以過點Q做輔助線QD⊥BP，通過PQ=QB可以得出BD的距離，然后根據相似三角形的定理，可以得出t的值。

第二種，做RT△OBC的斜邊中線OE這樣的值OE與BE相等，從而△OEB與△PQB為相似三角形，同樣也能得知t的值。

第三種，在RT△PHQ中有OH2+PH2=PQ2所以可以求出t的值

近幾年的中考數學試卷當中，二次函數的動點問題一直以壓軸題的形式出現，同時也是將幾何與函數進行融合的一種題型，因此教師可以將此作為一個獨立模塊對學生進行針對性的教學，從而促進學生數學知識點掌握。

參考文獻

[1]二次函數圖像動點與相似三角形融合的中考題解決策略探究[J].中學數學，2020（06）：72-73+85.

[2]鄭博文.初中數學二次函數動點問題的教學策略研究[J].課程教育研究，2019（45）：131.