“兩點(diǎn)一線”初中數(shù)學(xué)小專題教學(xué)策略研究
陳凰
【摘要】當(dāng)前的初中數(shù)學(xué)教學(xué)狀況不甚理想,數(shù)學(xué)復(fù)習(xí)課中也普遍存在著“以練代講”的情況,導(dǎo)致復(fù)習(xí)課堂十分枯燥,教學(xué)效果不明顯,學(xué)生的數(shù)學(xué)核心素養(yǎng)也得不到良好的發(fā)展。為了解決低效復(fù)習(xí)的現(xiàn)狀,嘗試采取小專題教學(xué)策略。筆者在長期的教學(xué)實(shí)踐以及理論鉆研中,提出了“兩點(diǎn)一線”的小專題教學(xué)模式,并申請(qǐng)了梅州市市級(jí)課題進(jìn)一步研究,希望通過本論文的探討與分析,能夠?yàn)槌踔袛?shù)學(xué)教學(xué)工作者帶來一些啟發(fā)。
【關(guān)鍵詞】兩點(diǎn)一線 ? 初中數(shù)學(xué) ? 小專題教學(xué) ? 策略
初中數(shù)學(xué)復(fù)習(xí)課堂普遍存在著問題主線不清楚、學(xué)生參與度不高,數(shù)學(xué)思想方法提煉不夠等問題。如何解決這些問題是擺在我們數(shù)學(xué)教師面前的重要任務(wù)。2018年9月至今,我們教研組嘗試進(jìn)行了36節(jié)“兩點(diǎn)一線”的小專題復(fù)習(xí)課,深受學(xué)生們的歡迎與喜愛,取得了良好的效果。
一、“兩點(diǎn)一線”小專題的概念界定
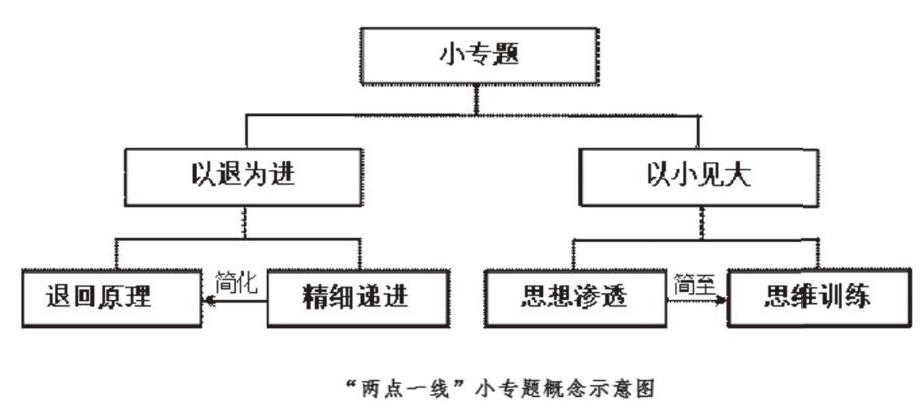
“兩點(diǎn)一線”小專題教學(xué):以解決一道中等題目為主基調(diào),先讓學(xué)生“退”到解決題目的基本概念或者原理進(jìn)行回歸性學(xué)習(xí),再用一條清晰的主線來串聯(lián)這些概念和原理,“進(jìn)”到原題中解決問題,即“以退為進(jìn)”;在設(shè)計(jì)上,要求簡化原題,通過設(shè)計(jì)學(xué)生最近發(fā)展區(qū)內(nèi)的簡單題目,以突出核心知識(shí),提高思維訓(xùn)練,即“以小見大”。
二、“兩點(diǎn)一線”初中數(shù)學(xué)小專題教學(xué)策略
下面以《小專題:一元二次方程根的判別式的應(yīng)用》復(fù)習(xí)課為例進(jìn)行闡述。
1.退回原理,喚起知識(shí)
在傳統(tǒng)的初中數(shù)學(xué)教學(xué)模式當(dāng)中,尤其是在復(fù)習(xí)的過程中,教師對(duì)概念和原理就很少側(cè)重,更加傾向于讓學(xué)生做大量的數(shù)學(xué)題來鞏固提高。教師認(rèn)為學(xué)生的問題是在于不會(huì)做一些復(fù)雜的題目,實(shí)際上這是因?yàn)閷W(xué)生的基礎(chǔ)知識(shí)沒有打牢,尤其是一些小的概念和數(shù)學(xué)原理。因此教師應(yīng)該要重視知識(shí)結(jié)構(gòu)與體系,以基礎(chǔ)的知識(shí)點(diǎn)來展開教學(xué),喚醒學(xué)生的記憶,從而為學(xué)生做一些復(fù)雜的數(shù)學(xué)題打下基礎(chǔ)。
為了讓學(xué)生了解一元二次方程根的個(gè)數(shù)基本分類,我先設(shè)計(jì)了幾道方程題,從最基本的原理入手,讓學(xué)生充分的自我探究。具體實(shí)施如下:首先將班內(nèi)學(xué)生分成了三組,讓學(xué)生分別就(1)X2+2X=8;(2)X2-X=0;(3)X2-X=-2進(jìn)行探究,最后分別得出(1)X=2,X=-4;(2)X=±1;(3)無實(shí)根。學(xué)生探究得出三個(gè)方程的根都不相同。此時(shí)我提出問題,退回原理,讓學(xué)生就方程的根為何不一樣再進(jìn)行探究,思考是否還存在其他情況。從基礎(chǔ)的知識(shí)點(diǎn)來展開復(fù)習(xí),讓學(xué)生能夠深刻領(lǐng)悟一元二次方程根的判別式相關(guān)概念,感悟基本原理的作用。
2.設(shè)計(jì)問題,精細(xì)遞進(jìn)
問題是思考的基礎(chǔ),也是學(xué)習(xí)的開始。古代孔子就十分注重利用問題來啟發(fā)學(xué)生,蘇格拉底也曾發(fā)明了“產(chǎn)婆術(shù)”的教學(xué)方法,主張給學(xué)生創(chuàng)造問題情境。“兩點(diǎn)一線”的小專題教學(xué)模式注重設(shè)計(jì)問題串啟發(fā)學(xué)生思考探究,讓學(xué)生在解決問題的過程中享受到碰撞思維的樂趣。教師通過設(shè)計(jì)層層遞進(jìn)的問題,在學(xué)生認(rèn)知特點(diǎn)和學(xué)習(xí)能力的基礎(chǔ)上設(shè)計(jì)層次性的問題,讓學(xué)生逐步地得到提高。
例如,在復(fù)習(xí)一元二次方程的判別式后,以問題的形式實(shí)施了精細(xì)遞進(jìn)。關(guān)于x的一元二次方程kx2-2x-1=0
(1)若方程有兩個(gè)相等的實(shí)數(shù)根,則k取值范圍是_______。
(2)若方程有實(shí)數(shù)根,則k取值范圍是_______。
(3)若方程沒有實(shí)數(shù)根,則k取值范圍是_______。
讓學(xué)生在由淺入深的思考過程中進(jìn)行歸納總結(jié),要求待定系數(shù)的取值范圍則通過判別式來進(jìn)行計(jì)算,通過遞進(jìn)的問題增強(qiáng)學(xué)生思考解題的能力。
3.總結(jié)提煉,思想滲透
在課程改革的背景之下,要充分發(fā)揮數(shù)學(xué)思想的重要性。數(shù)學(xué)思想是解決數(shù)學(xué)問題的一個(gè)有力武器,同時(shí)也是數(shù)學(xué)核心素養(yǎng)的重要組成部分。小專題教學(xué)講究數(shù)學(xué)練習(xí)題的質(zhì)量,讓學(xué)生在做題的過程中總結(jié)數(shù)學(xué)思想方法,這樣能以小見大,因?yàn)榧幢闶窃趶?fù)雜的數(shù)學(xué)問題,只要掌握了數(shù)學(xué)思想方法,也就很容易解決。
例如,在總結(jié)本節(jié)課時(shí),隨機(jī)找學(xué)生談一談自己在本節(jié)課有哪些收獲?這樣學(xué)生會(huì)自己主動(dòng)思考總結(jié)知識(shí)點(diǎn),圍繞本節(jié)課的復(fù)習(xí)內(nèi)容(1)一元二次方程根的判別式的意義;(2)由根的判別式的符號(hào)判斷一元二次方程根的情況等主題進(jìn)行回答,對(duì)于一些知識(shí)點(diǎn)誤區(qū)教師進(jìn)行適當(dāng)點(diǎn)撥。最后教師再特別強(qiáng)調(diào)一下本節(jié)課要掌握分類討論思想、數(shù)形結(jié)合思想等,從而達(dá)到自己的預(yù)期教學(xué)效果。
4.題型鞏固,思維訓(xùn)練
相比于數(shù)學(xué)思想方法,對(duì)于學(xué)生來說數(shù)學(xué)思維能力可能更加抽象化。數(shù)學(xué)思維能力是包括思維的敏捷性、靈活性、批判性、廣闊性、深刻性等,教師應(yīng)該借助一些典型的題型,來幫助學(xué)生進(jìn)行思維訓(xùn)練。例如,不解方程式,只需用b2-4ac的值>0、<0、=0的情況判定方程根的情況。如:(1) 12x+x2=3,(2)6x2+2x+1=0,(3)4x2-x+8=0,(4) x2-7x-18=0。通過題型鞏固來使學(xué)生判別方程是否有實(shí)根和兩個(gè)實(shí)根是否相等,弄懂為什么可以用判別式判別一元二次方程根的情況。
總而言之,在初中數(shù)學(xué)教學(xué)中進(jìn)行“兩點(diǎn)一線”小專題教學(xué),不僅能夠改變傳統(tǒng)的復(fù)習(xí)課堂模式,也能夠激發(fā)學(xué)生的數(shù)學(xué)思維,同時(shí)對(duì)促進(jìn)教師的專業(yè)素養(yǎng)也有著重要的意義。
【參考文獻(xiàn)】
[1]沈岳夫.知識(shí)與能力并重 思想與經(jīng)驗(yàn)齊驅(qū)——初中數(shù)學(xué)專題復(fù)習(xí)“組塊式”教學(xué)模式初探[J].中學(xué)數(shù)學(xué)雜志,2013(10):17-19.
[2]王蕓,韓龍淑.PCK視角下的初中數(shù)學(xué)專題復(fù)習(xí)課解析——以概率專題復(fù)習(xí)課為例[J].中國數(shù)學(xué)教育,2019(Z3):42-45.

